1757
Going beyond the image space: undersampled MRI reconstruction directly in the k-space using a complex valued residual neural network1Department of Biomedical Magnetic Resonance, Otto von Guericke University, Magdeburg, Germany, 2Data and Knowledge Engineering Group, Otto von Guericke University, Magdeburg, Germany, 3Faculty of Computer Science, Otto von Guericke University, Magdeburg, Germany, 4Institute of Medical Engineering, Otto von Guericke University, Magdeburg, Germany, 5MedDigit, Department of Neurology, Medical Faculty, University Hopspital, Magdeburg, Germany, 6German Centre for Neurodegenerative Diseases, Magdeburg, Germany, 7Center for Behavioral Brain Sciences, Magdeburg, Germany, 8Leibniz Institute for Neurobiology, Magdeburg, Germany
Synopsis
One of the common problems in MRI is the slow acquisition speed, which can be solved using undersampling. But this might result in image artefacts. Several deep learning based techniques have been proposed to mitigate this problem. Most of these methods work only in the image space. Fine anatomical structures obscured by artefacts in the image can be challenging to reconstruct for a model working in the image space, but not in k-space. In this research, a novel complex-valued ResNet has been proposed to work directly in the k-space to reconstruct undersampled MRI. The preliminary experiments have shown promising results.
Introduction
MRI provides excellent soft tissue contrasts but suffers from slow acquisition speed which can be improved using undersampling. However, this might leads to artefacts or in loss of image resolution. Various methods have been proposed to reconstruct undersampled images using deep learning techniques, but they mainly work in the image space1,2,3. When the images are already heavily corrupted by artefacts, it might be difficult for a network to reconstruct fine structures which are not visible because of the obscurity caused by those artefacts. When it comes to the k-space, there are only missing data and no obscurity. With this thing in mind, this can be hypothesized that if the network directly works in the k-space, then the network will be able to reconstruct even the fine structures which are obscured in the undersampled. AUTOMAP4 was proposed to work directly in the k-space and provide image space as output. But the network design is a hindrance to scalability when it comes to images with higher matrix sizes. There were a few more research in this direction5,6, but they are based on real-valued convolutions, by converting the complex-valued k-space data into two channel (real and imaginary) real-valued data. Trabelsi et al.7 has introduced the possibility of using complex valued convolutions. This work aims to reconstruct undersampled MRIs directly in the k-space by using a residual network (ResNet) architecture based on complex-valued convolutions.Methodology
In complex-valued convolutions7, the filters (kernels) of the network consist of real and imaginary parts. These complex kernels are applied on the input following the following equations:FMR = (IR * KR) - (II * KI)
FMI = (IR * KI) + (II * KR)
Where, IR and II represent the real and imaginary part of the input, KR and KI represent the real and imaginary part of the kernels, * denotes the convolution operator, and finally FMR and FMI represent the real and imaginary part of the resultant feature maps respectively.
The network model was created by taking inspirations from the residual blocks of the RecoResNet3. The proposed model consists of a series of residual blocks, each comprises of two complex valued convolutions with a kernel size of three, stride of one and padding of one; separated by a AdaptiveCmodReLU8 for non-linearity. The AdaptiveCmodReLU computes the complex modulus ReLU of the complex input while learning a threshold value. The input to each of the residual blocks were added with its output as residue, hence it is called residual network. The undersampled k-space was supplied as input to the network and the network provided an output k-space. The real acquired data present in the undersampled k-space were replaced in the output k-space for data consistency, creating the final output k-space. 2D inverse fast Fourier transform was performed on this output k-space to generate the reconstructed image and on the fully-sampled k-space to generate the ground-truth image. Finally, the loss was calculated using L1 loss by comparing the reconstructed image with the ground-truth image. The network architecture can be seen in Fig.1. The network was implemented using PyTorch and pytorch-complex9 package.
The preliminary experiments with the network were performed using the fastMRI10 T2 Axial brain dataset. The network was worked directly with coil-wise images. During inference, the final coil-images were combined using sum-of-squares to obtain the final output image. Two different undersampling patterns with an acceleration factor of 4 were experimented with: random variable density sampling with a centre fraction of 0.08 and by taking only the centre of the k-space with full phase-encoding lines.
Results
Fig.2 and Fig.3. show the results for qualitative analysis, for the reconstruction of random variable density undersampling and centre of the k-space sampling. For the random variable density undersampling, it can be observed that the network was able to reconstruct the image close to the ground-truth. For the centre k-space sampling, the network was able to reconstruct the image, but with a few remaining undersampling artefacts. While performing qualitative analysis, the network achieved an SSIM of 0.908±0.110 (improving from 0.788±0.081) and 0.916±0.128 (improving from 0.800±0.088) for both the sampling patterns respectively. The best resultant image produced an SSIM of 0.955 (improving from 0.877) and 0.954 (improving from 0.882) for the sampling patterns respectively.Conclusion
This work presented a novel complex residual network (ResNet) architecture for undersampled MR reconstruction while directly working in the k-space. The network has shown promising results in terms of reducing artefacts and making the images sharper in comparison to the undersampled (zero-padded) images. However, some remaining artefacts were observed in the results, which demands further investigations. The quantitative analysis resulted in less than optimal score because the test set also contained some fully sampled images with only minor parts of the brain and are also noisy. Further experimentations will also be performed to check the model’s performance while reconstructing higher acceleration factors and different sampling patterns.Acknowledgements
This work was conducted within the context of the International Graduate School MEMoRIAL at Otto von Guericke University (OVGU) Magdeburg, Germany, kindly supported by the European Structural and Investment Funds (ESF) under the programme "Sachsen-Anhalt WISSENSCHAFT Internationalisierung“ (project no. ZS/2016/08/80646).References
1. Wang, Shanshan, et al. "Accelerating magnetic resonance imaging via deep learning." 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). IEEE, 2016.
2. Hyun, Chang Min, et al. "Deep learning for undersampled MRI reconstruction." Physics in Medicine & Biology 63.13 (2018): 135007.
3. Soumick Chatterjee, Mario Breitkopf, Chompunuch Sarasaen, Georg Rose, Andreas Nürnberger, and Oliver Speck. A deep learning approach for reconstruction of undersampled cartesian and radial data. In ESMRMB 2019, At Rotterdam.
4. Zhu, Bo, et al. "Image reconstruction by domain-transform manifold learning." Nature 555.7697 (2018): 487-492.
5. Eo, Taejoon, et al. "KIKI‐net: cross‐domain convolutional neural networks for reconstructing undersampled magnetic resonance images." Magnetic resonance in medicine 80.5 (2018): 2188-2201.
6. Han, Yoseo, Leonard Sunwoo, and Jong Chul Ye. "k-Space Deep Learning for Accelerated MRI." IEEE transactions on medical imaging 39.2 (2019): 377-386.
7. Trabelsi, C., Olexa Bilaniuk, Dmitriy Serdyuk, Sandeep Subramanian, J. F. Santos, Soroush Mehri, N. Rostamzadeh, Yoshua Bengio and C. Pal. “Deep Complex Networks.” ICLR 2018.
8. Scardapane, Simone, et al. "Complex-valued neural networks with nonparametric activation functions." IEEE Transactions on Emerging Topics in Computational Intelligence (2018).
9. https://pypi.org/project/pytorch-complex/
10. Zbontar, Jure, et al. "fastMRI: An open dataset and benchmarks for accelerated MRI." arXiv preprint arXiv:1811.08839 (2018).
Figures
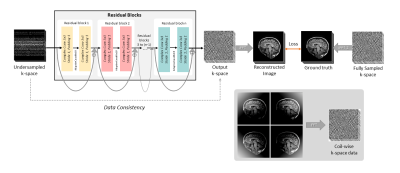
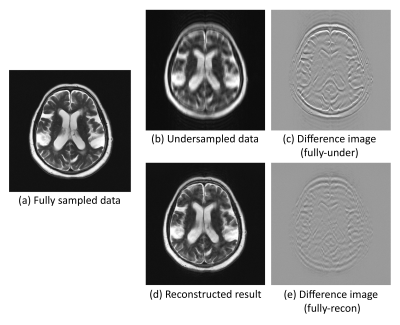
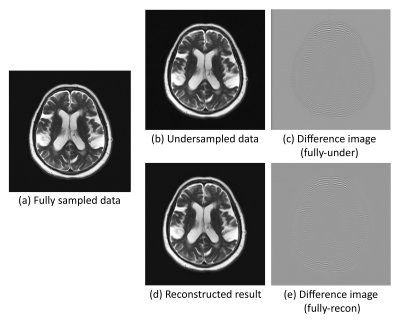
Fig.3: Reconstruction result of the centre k-space sampling, along with the fully-sampled image, undersampled (zero-padded) image and the corresponding difference images.