1752

PCA and U-Net based Channel Compression for Fast MR Image Reconstruction

Madiha Arshad¹, Mahmood Qureshi¹, Omair Inam¹, and Hammad Omer¹
¹Medical Image Processing Research Group (MIPRG), Department of Electrical and Computer Engineering, COMSATS University, Islamabad, Pakistan

Synopsis

In parallel imaging, the array coil with a large number of channels accelerates the data acquisition speed and provides high quality reconstructed images at the cost of an increase in computational complexity, image reconstruction time and memory requirement. Recently, Principal Component Analysis (PCA) has been used to compress multiple physical channels to a few virtual channels. However, the results showed a degradation in image quality and loss of sensitivity information. We introduce a novel channel compression technique combining PCA and U-Net before Compressed Sensing MRI reconstruction. The experimental results show less channel compression losses and retention of coil sensitivity information.

Introduction

Parallel Imaging (PI)¹ is a robust method for accelerating the MRI data acquisition process by acquiring under-sampled k-space data from multi-channel receiver coil arrays with unique sensitivity profiles. PI has been further accelerated by the use of Compressed Sensing-MRI (CS-MRI)² because it has the potential to reconstruct an image from highly under-sampled k-space multi-coil data. One major limitation of CS-MRI² is long image reconstruction time due to iterative nature of the reconstruction process. Moreover, the processing of massive MRI data as a result of increase in the number of channels in receiver coil array results in an increase in computational complexity and memory requirements. To mitigate the above said problems, PCA based channel compression³ has been suggested in recent literature. However, the results showed huge compression losses as the individual virtual coil images are of degraded quality and the corresponding virtual sensitivity maps are inhomogeneous⁴. In this paper, we propose a novel channel compression approach by combining PCA and deep learning, prior to CS-MRI reconstruction of MR images from Variable Density (VD) under-sampled data (Acceleration Factor (AF)=2).

Method

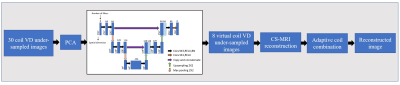
A deep learning algorithm (Figure-1) is proposed to compress the 30 channel receiver coil VD under-sampled images into 8 virtual coil VD under-sampled images prior to CS-MRI reconstruction². Firstly, PCA³ is applied to compress the VD under-sampled human head images from 30 channel receiver coils to 8 virtual coils. Later, U-Net⁵ is used to compensate the compression losses of PCA-based channel compression³. The U-Net provides final compressed 8 virtual coil VD under-sampled images. The U-Net is trained by using 200 datasets and tested by 20 datasets. The dataset is created by simulating the multi-receiver coil images from the acquired single-coil T2 weighted human head images⁷ (acquired from 1.5T scanner) by using the 30 and 8 receiver coil sensitivities estimated by Biot Savart Law⁸. For generating the input images, PCA³ is applied on the 30 channel receiver coil VD under-sampled images to get 8 virtual coil VD under-sampled images. These 8 virtual coil VD under-sampled images obtained from PCA³ are used as input and 8 channel receiver coil VD under-sampled images obtained from Biot Savart law⁸ are used as label.

For training, all the weights of the convolutional layers were initialized by a zero-centered normal distribution with a standard deviation of 0.05 without a bias term. The loss function of Mean Square Error was minimized by using the RMSPropOptimizer with a learning rate of 0.001, mini-batch size 2, and 1000 epochs. Training was performed on Python 3.7.1 by Keras using TensorFlow as a backend on Intel(R) core (TM) i7-4790 CPU, clock frequency 3.6GHz, 16 GB RAM and GPU NVIDIA GeForce GTX 780 for approximately twelve hours.

After compression, CS-MRI² is used for coil-by-coil reconstruction of the 8 virtual coil VD under-sampled images obtained from the proposed method. Later, adaptive coil combination⁹ of the 8 reconstructed virtual coil images provides the final image. The results are compared against the adaptive coil combination of the CS-MRI reconstructed 8 virtual coil images obtained from PCA-based channel compression³.

Results

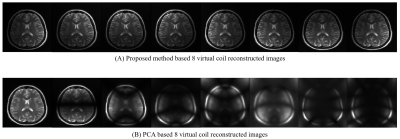
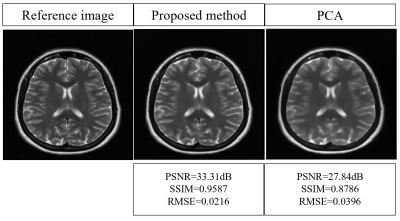
Figure-1 shows a block diagram of the proposed method. Figure-2 shows the 8 virtual coil reconstructed images obtained from the proposed method and PCA respectively. Figure-3 shows the sensitivity maps (estimated by Eigen value method⁶) of the 8 virtual coil reconstructed images obtained from the proposed method and PCA respectively. Figure-4 shows the adaptive coil combination of the virtual coil reconstructed images obtained from the proposed method and PCA respectively. An adaptive coil combination of the fully sampled 30 channel receiver coil images are used as reference images.

Discussion and Conclusion

The virtual coil images obtained from the proposed method retain the coil sensitivity information better as compared to that of PCA. An improvement of 19.64%, 9.11% and 45.45% is seen in the PSNR, SSIM and RMSE values respectively of the final reconstructed images obtained from the proposed method as compared to PCA in our experiments. These results show the success of our proposed channel compression in reducing the size of the input data before reconstruction while preserving the benefits of data acquisition from multiple channels.

Acknowledgements

No acknowledgement found.

References

1. Hamilton J, Franson D, Seiberlich N. Recent advances in parallel imaging for MRI. Progress in Nuclear Magnetic Resonance Spectroscopy. 2017;101(216):71–95. doi:10.1016/j.pnmrs.2017.04.002

2. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine. 2007;58(6):1182–1195. doi:10.1002/mrm.21391

3. Inam O, Qureshi M, Malik SA, Omer H. Iterative Schemes to Solve Low-Dimensional Calibration Equations in Parallel MR Image Reconstruction with GRAPPA. BioMed Research International. 2017;2017. doi:10.1155/2017/3872783

4. Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magnetic Resonance in Medicine. 2007;57(6):1131–1139. doi:10.1002/mrm.21237

5. Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In: Navab N, Hornegger J, Wells WM, Frangi AF, editors. Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2015. Cham: Springer International Publishing; 2015. p. 234–241.

6. Irfan AS, Nisar A, Shahzad H, Omer H. Sensitivity Maps Estimation Using Eigenvalues in Sense Reconstruction. Applied Magnetic Resonance. 2016;47(5):487–498. doi:10.1007/s00723-016-0767-7

7. Hyun CM, Kim HP, Lee SM, Lee S, Seo JK. Deep learning for undersampled MRI reconstruction. Physics in Medicine and Biology. 2018;63(13):aac71a. https://doi.org/10.1088/1361-6560/aac71a. doi:10.1088/1361-6560/aac71a

8. Guerquin-Kern M. Matlab code for MRI simulation and reconstruction. 2012:8. http://bigwww.epfl.ch/algorithms/mri-reconstruction

9. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magnetic Resonance in Medicine. 2000;43(5):682–690. doi:10.1002/(SICI)1522-2594(200005)43:5<682::AID-MRM10>3.0.CO;2-G

Figures

Figure 1: Block diagram of the proposed method: First, PCA is applied to compress the VD under-sampled human head data from 30 channel receiver coils to 8 virtual coils. Later U-Net is used to compensate the compression losses of PCA in terms of sensitivity information of 8 virtual coils VD under-sampled images. Later, adaptive coil combination of CS-MRI reconstructed virtual coil images gives the final solution/reconstructed image.

Figure 2: CS-MRI reconstructed 8 virtual coil images obtained from the proposed channel compression and PCA: First the VD under-sampled human head data (AF=2) is compressed from 30 channel receiver coils into 8 virtual coils by the proposed method and PCA. Later, CS-MRI is used for coil-by-coil reconstruction of 8 virtual coil under-sampled images. The reconstructed virtual coil images show minimum compression losses by the proposed method as compared to the PCA.

Figure 3: Sensitivity maps (estimated by Eigen value method) of 8 virtual coil reconstructed images obtained from the proposed method and PCA. These maps indicate the spatial information of the virtual receiver coils. In the proposed method, the virtual sensitivity maps give us an illusion of a circular alignment of the virtual coils just like in the case of data acquisition from a circular alignment of the original physical coils whereas in PCA, the virtual sensitivity maps are inhomogeneous.

Figure 4: Adaptive coil combination of the 8 virtual coil reconstructed images obtained from the proposed method and PCA. These results are compared against the reference image i.e. adaptive coil combination of the 30 channel receiver coil fully sampled images. The results obtained from the proposed method are of high quality as indicated by PSNR, SSIM and RMSE values.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1752