1751
Rethinking complex image reconstruction: ⟂-loss for improved complex image reconstruction with deep learning
Maarten Terpstra1,2, Matteo Maspero1,2, Jan Lagendijk1, and Cornelis A.T. van den Berg1,2
1Department of Radiotherapy, University Medical Center Utrecht, Utrecht, Netherlands, 2Computational Imaging Group for MR diagnostics & therapy, University Medical Center Utrecht, Utrecht, Netherlands
1Department of Radiotherapy, University Medical Center Utrecht, Utrecht, Netherlands, 2Computational Imaging Group for MR diagnostics & therapy, University Medical Center Utrecht, Utrecht, Netherlands
Synopsis
The \(\ell^2\) norm is the default loss function for complex image reconstruction. In this work, we investigate the behavior of the \(\ell^1\) and \(\ell^2\) loss functions for complex image reconstruction with non-complex-valued models. Simulations show that these norms assign a lower loss to reconstructions with lower magnitude, introducing an asymmetry in the loss function. To address this, we propose a new, symmetric loss function, and train deep learning models to show that the proposed loss function achieves better performance and faster convergence on complex image reconstruction tasks.
Introduction
The acquired MR signal is an inherently complex signal, consisting of magnitude and phase information. Complex image reconstruction enables both high-quality magnitude reconstructions while simultaneously providing phase maps, which are useful for applications such as motion estimation, QSM, or susceptibility-weighted imaging\(^1\).Complex images can be reconstructed with a fully complex-valued network\(^2\). However, this is computationally demanding and scarce implementations are available; as a result, reconstruction tasks are usually learned with a non-complex-valued network. The loss functions generally adopted for these networks usually minimize the \(\ell^1\)-norm or \(\ell^2\)-norm independently over the real and imaginary channels.
In this work, we investigate possible drawbacks of \(\ell^p\)-norm on complex images by simulation, proposing and investigating the performance of a new loss function that uses both magnitude and phase information for complex image reconstructions.
Theory
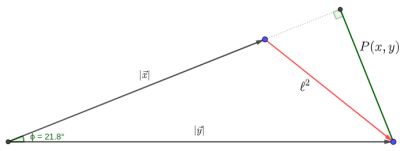
With supervised image reconstruction, a real-valued deep learning model is often optimized by minimizing \[\ell^2(x,y)=\vert\vert f_\theta(x)-y\vert\vert_2^2=\sqrt{(\operatorname{Re}(x)-\operatorname{Re}(y))^2+(\operatorname{Im}(x)-\operatorname{Im}(y))^2}\] i.e. the \(\ell^2\)-norm minimizes independent terms over the real and imaginary channels.If we consider complex numbers with non-zero magnitude as vectors (i.e. phasors), the \(\ell^2\) can be interpreted as minimizing the magnitude of the difference vector between \(\vec{x}\) and \(\vec{y}\), illustrated in Figure 1.
We can rewrite this using the law of cosines as \[\ell^2(\vec{x},\vec{y})=\sqrt{\vert \vec{x}\vert^2+\vert \vec{y}\vert^2-2\vert\vec{x}\vert\vert\vec{y}\vert\cos{\phi}}=\sqrt{(1+\lambda^2-2\lambda\cos\phi)\vert\vec{y}\vert^2}\]with \(\lambda=\frac{\vert\vec{x}\vert}{\vert\vec{y}\vert}\rightarrow\vert\vec{x}\vert=\lambda\vert\vec{y}\vert\) and \(\phi=\operatorname{atan2}(\vec{y},\vec{x})\).
The \(\ell^2\)-norm depends quadratically on \(\lambda\), giving rise to an asymmetric loss with respect to \(\lambda\) as \(\ell^2_{\lambda<1}\) is smaller than \(\ell^2_{\lambda>1}\). As models rarely converge on the global minimum of a loss landscape for a dataset (i.e. models almost always converge with non-zero loss), a model trained with an \(\ell^2\) loss thus may prefer reconstructions with \(\lambda<1\), privileging reconstructions with lower image magnitude.
We propose a loss function that is symmetric around \(\lambda\), called \(\perp\)-loss (perpendicular-loss) hypothesizing that this may be beneficial for complex image reconstruction. This loss is defined as: \[\perp(\vec{x},\vec{y})=P(\vec{x},\vec{y})+\ell^1(\vert\vec{x}\vert,\vert\vec{y}\vert)\] with \(P(\vec{x},\vec{y})=\frac{\vert\operatorname{Re}(x)\operatorname{Im}(y)-\operatorname{Im}(x)\operatorname{Re}(y)\vert}{\vert\vec{y}\vert}\), which is the length of the segment starting at \(\vec{y}\) perpendicular to \(\vec{x}\), as shown in Figure 1.
Methods
To investigate the asymmetric behavior of the loss functions with respect to \(\lambda\), we evaluated the loss landscape of loss functions on pairs of complex numbers with known \(\lambda\) and \(\phi\). Per \((\phi, \lambda)\) pair, \(10^5\) vectors were calculated. To test the behavior of the loss functions with a deep learning reconstruction task, we trained three end-to-end variational models3, minimizing the \(\ell^{1}\), \(\ell^{2}\), or the \(\perp\)-loss for 2D complex images. The networks consisted of 6 cascades and were trained deterministically to prevent performance differences due to initialization.The networks were trained on the Multi-channel MR Image Reconstruction Challenge dataset4, with 3D T1-weighted complex brain MRIs acquired with a gradient-recalled echo sequence (resolution=1.0x1.0x1.0 mm3) using 12 receive channels. Data was coil-combined using an adaptive combination algorithm5 and normalized to [0,1] image magnitude. In total, all models were trained on 6240 2D slices of 40 subjects and tested on 2495 slices of 16 subjects.
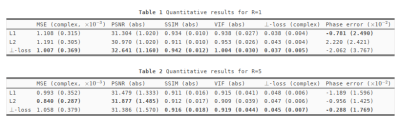
Three models were trained for 20 epochs on fully-sampled k-space and three models were trained for 100 epochs on five-fold accelerated k-space using variable-density Poisson sampling masks using Adam6 (lr=10-3). Each model was evaluated using the mean and standard deviation of the PSNR, SSIM7, VIF8 and phase error, i.e. the mean residual angle. A Wilcoxon rank-sum test was used for these metrics comparing the \(\ell^1\) and \(\ell^2\) reconstructions against \(\perp\)-loss.
Results and discussion
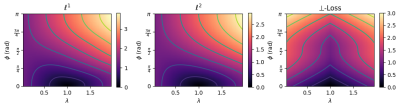
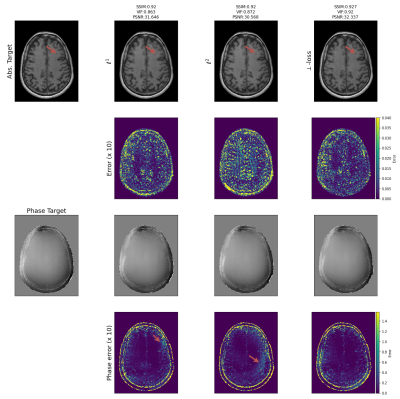
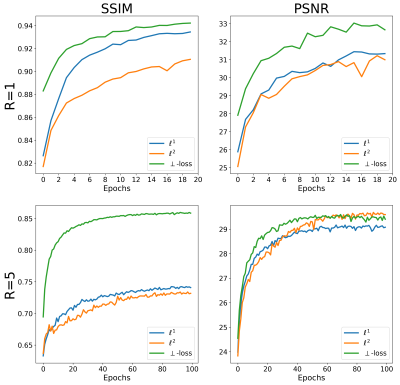
The loss landscape shows that \(\ell^p\) is affected by an asymmetry w.r.t. \(\lambda\), assigning a lower loss to \(\lambda<1\). The proposed \(\perp\)-loss is symmetric (Figure 2). Typical reconstructions from a deep learning model trained with \(\perp\)-loss are of slightly higher quality than those with \(\ell^p\) losses (Figure 3). A quantitative evaluation of the validation set shows that \(\perp\)-loss outperforms the \(\ell^1\) and \(\ell^2\) norm on the SSIM, VIF and phase error metrics (Wilcoxon, \(p\ll 0.01\)), increasing the SSIM with more than 0,13 over the entire field of view and with 0,04 within an anatomy mask with R=5 (Figure 4, top). Also, \(\perp\)-loss achieves a nearly four times lower phase error. The test loss as a function of the number of epochs show that \(\perp\)-loss converges faster–in approximately half the epochs–compared to the network trained on \(\ell^2\): 45 epochs for \(\perp\)-loss against 95 epochs for \(\ell^2\) at R=5 (Figure 5).On the one hand, the \(\perp\)-loss improves magnitude image reconstruction; on the other hand, it provides also higher-quality phase maps than real-valued models (Figure 4, bottom). Earlier works also attempted to address limitations of the \(\ell^2\) norm\(^{9}\), suggesting the use of local SSIM to improve \(\ell^2\) performances. The \(\perp\)-loss may be further extended to incorporate local statistics rather than pixel statistics. In future work, we also intend to evaluate this method on fully complex networks\(^2\). Also, we would like to investigate performance of our loss function with different models, datasets, optimizers, regularization schemes, and other training hyperparameters.Conclusion
We propose a novel loss function for complex image reconstruction, called \(\perp\)-loss, that is symmetric with respect to the ratio of magnitude vectors. We demonstrated that it improves magnitude and phase MRI reconstruction. \(\perp\)-loss achieved the same performance as \(\ell^1\) or \(\ell^2\) in approximately half the training time, or higher performance with the same training time.Acknowledgements
This work is part of the research programme HTSM with project number 15354, which is (partly) financed by the Netherlands Organisation for Scientific Research (NWO) and Philips Healthcare. We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Quadro RTX 5000 GPU used for prototyping this research.References
[1] Brown, Robert W., et al. Magnetic resonance imaging: physical principles and sequence design, chapter 25, John Wiley & Sons, 2014.
[2] Amin et al. "Wirtinger calculus based gradient descent and levenberg-marquardt learning algorithms in complex-valued neural networks." International Conference on Neural Information Processing. 2011.
[3] Sriram et al. "End-to-End Variational Networks for Accelerated MRI Reconstruction." (2020).
[4] Beauferris et al. "Multi-channel MR Reconstruction (MC-MRRec) Challenge--Comparing Accelerated MR Reconstruction Models and Assessing Their Genereralizability to Datasets Collected with Different Coils." (2020).
[5] Inati et al. Proc. "A Fast Optimal Method for Coil Sensitivity Estimation and Adaptive Coil Combination for Complex Images" Intl. Soc. Mag. Reson. Med 2014
[6] Kingma et al. "Adam: A method for stochastic optimization." arXiv preprint arXiv:1412.6980 (2014).
[7] Wang, Zhou, et al. "Image quality assessment: from error visibility to structural similarity." IEEE transactions on image processing 13.4 (2004).
[8] Sheikh et al.. "A visual information fidelity approach to video quality assessment." The First International Workshop on Video Processing and Quality Metrics for Consumer Electronics. Vol. 7. sn, 2005.
[9] Hammernik et al. " L2 or not L2: Impact of Loss Function Design for Deep Learning MRI Reconstruction" Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
Figures
Figure 1: Geometrical representation of loss functions. We have two vectors, \(\vec{x}\) and \(\vec{y}\), in the complex plane with magnitude \(|\vec{x}|\) and \(|\vec{y}|\) separated by an angle ϕ. the \(\ell^2\) norm minimizes the red diagonal. Our proposed loss function is defined as \(\perp(\vec{x},\vec{y})=P(\vec{x},\vec{y})+\ell^1(\vert \vec{x}\vert,\vert \vec{y}\vert)\). It minimizes the angle error by minimizing \(P(\vec{x},\vec{y})\) , i.e. the green line perpendicular to \(\vec{x}\), in conjunction with the \(\ell^1\) loss of vector magnitude.
Figure 2: Simulation of loss landscapes. The loss landscapes of the \(\ell^1, \ell^2,\) and \(\perp\)-loss are shown, respectively. For every \((\phi, \lambda)\) pair, \(10^5\) random complex number pairs were generated. Contours show lines of equal loss. The figures show that \(\perp\)-loss is symmetric around \(\lambda\), whereas the \(\ell^1\) and \(\ell^2\) loss functions have a higher loss for \(\lambda > 1\).
Figure 3: Typical reconstructions. Typical magnitude reconstructions from the \(\ell^1\), \(\ell^2\) and \(\perp\)-loss networks with R=5. Top row shows magnitude target and reconstructions, with respective squared error maps below. The training with our loss function reconstructs smaller details as highlighted by the red arrows. Third row shows phase map target and reconstructions, with respective error maps below. Significant phase artifacts not present in \(\perp\)-loss are highlighted.
Figure 4: Quantitative results. The evaluation of multiple metrics for the three identical models trained with different loss functions within an anatomy mask. Best results per metric are highlighted in boldface. All differences are statistically significant (Wilcoxon, \(p \ll 0.01\))
Figure 5: Test results per epoch. The evaluation on the test set per epoch. Top row shows results on fully-sampled data, while the bottom row shows results on five-fold undersampled data. Metrics are evaluated over the entire field of view.