1729
Measurement of radiofrequency absorption and thermal diffusion coefficients of brain tissue
David H Gultekin1, Peter H Siegel2,3, John T Vaughan1, and John C Gore4
1Zuckerman Mind Brain Behavior Institute, Columbia University, New York, NY, United States, 2Jet Propulsion Laboratory, National Aeronautics and Space Administration, Pasadena, CA, United States, 3Department of Electrical Engineering, California Institute of Technology, Pasadena, CA, United States, 4Vanderbilt University Institute of Imaging Science, Nashville, TN, United States
1Zuckerman Mind Brain Behavior Institute, Columbia University, New York, NY, United States, 2Jet Propulsion Laboratory, National Aeronautics and Space Administration, Pasadena, CA, United States, 3Department of Electrical Engineering, California Institute of Technology, Pasadena, CA, United States, 4Vanderbilt University Institute of Imaging Science, Nashville, TN, United States
Synopsis
A method is introduced to measure the absorption coefficient and the thermal diffusion coefficient of ex vivo brain tissue exposed to radiofrequency radiation emitted from a half wavelength dipole antenna and a rectangular waveguide using MRI and thermocouples. By analyzing the spatial and temporal variations of thermal gradients, it is possible to measure simultaneously both the absorption coefficient and the thermal diffusion coefficient in brain tissue in a single experiment.
Purpose
In magnetic resonance imaging (MRI), the absorption of radiofrequency (RF) energy and thermal diffusion are important for the characterization of tissues and for accurate estimates of heating effects and safety. The absorption and diffusion of RF energy cause thermally induced spatial and temporal variations of MRI parameters during the course of imaging. These effects in brain tissue are described quantitatively by the absorption coefficient ($$$\alpha$$$) and thermal diffusion coefficient ($$$D$$$). The absorption coefficient is dependent on wavelength ($$$\lambda$$$) and determines the heat deposited in tissue with depth of penetration. The absorbed heat then diffuses through the tissue, potentially changing the temperature at a distance from the original energy deposition. While such effects can be calculated based on models, a method to visualize the RF energy absorption and thermal diffusion would have practical uses.Methods
We use two methods, MRI and embedded thermocouple arrays (TCA), to measure the absorption coefficient and thermal diffusion coefficient of ex vivo bovine brain tissue exposed to radiation from two different RF sources, a 1.9 GHz half wavelength dipole antenna ($$$\lambda/2$$$) and a 1.9 GHz rectangular waveguide (WR). The half wavelength dipole antenna was used as the RF source for MRI because it involved only small metallic components, while the rectangular waveguide was used with the TCA experiments because it required larger metallic components but provided more controlled beam properties and uniform source power. Both arrangements are shown in Figure 1. In the MRI measurements, a 3T MRI (Signa HDx, version LX14.0, GEMS) and a birdcage head coil (GEMS, 3T/94) were used to acquire spin phase shift images using a fast gradient echo (GRE) sequence, with two echoes; echo times (TE), 2.4 and 5.8 ms; bandwidth (BW), 125 kHz; repetition time (TR), 90 ms; matrix, 128 x 256; field of view (FOV), 180 mm x 180 mm. Two imaging protocols with variations of spatial and temporal resolutions were tested with the following parameters: slice thickness, 2.5 mm and 5 mm; number of slices, 18 and 10; slab thickness, 45 mm and 50 mm; number of phases, 37 and 75, spatial resolution, 0.7 x 0.7 x 2.5 mm3 and 0.7 x 0.7 x 5 mm3; temporal resolution 25 s and 11.5 s, respectively. For the RF waveguide measurements, a signal generator (HP 8340A) was coupled to a traveling wave tube (TWT) amplifier (5SIG4, AR World) and the rectangular waveguide (WR-430, pass band 1.7-2.6 GHz, ID: 109.2 x 54.6 mm) to deliver 1.9 GHz RF energy to the brain tissue. The type T thermocouples (IT-18 or IT-23, Physitemp, NJ) embedded in the tissue along the x axis and positioned at the depths of 1, 6, 11, 16 and 21 mm were used to measure the temperature vs. depth with 1 Hz sampling frequency in the brain tissue in the TCA experiments. The MRI temperature maps obtained from spin phase shift imaging for two different brain tissues in two different experiments are shown in Figure 2. The spatial and temporal variations of temperature in the brain tissue subjected to radiofrequency heating at 1.9 GHz were acquired and analyzed for comparison.The semi-infinite heat conduction equation in one dimension with a constant flux boundary condition is
$$\frac{\partial T}{\partial t}=D\frac{\partial^2 T}{\partial x^2},\quad x > 0,\quad T(x,0) = cons., \quad t > 0,\quad f=f_0exp\left(-\alpha x\right)$$
where $$$f$$$ is the power density varying with depth, $$$f_0$$$ is the incident surface power density, $$$\alpha$$$ is the absorption coefficient. The solution of this equation with initial and boundary conditions results in variation of temperature in time and one dimension as
$$T(x,t)=\frac{c}{\alpha}\left[2\alpha\cdot d\cdot \textrm{ierfc} \left(\frac{1}{2}\frac{x}{d}\right)-\exp \left(-\alpha x\right)+\frac{1}{2} \exp\left(\alpha^2d^2-\alpha x\right) \cdot \textrm{erfc}\left(\alpha d -\frac{1}{2}\frac{x}{d}\right)+\frac{1}{2} \exp\left(\alpha^2d^2+\alpha x\right) \cdot \textrm{erfc}\left(\alpha d +\frac{1}{2}\frac{x}{d}\right)\right]$$
where $$$d=\sqrt {Dt}$$$ is the half root mean square diffusion length (m), $$$c=f_0/\kappa$$$ is a constant and $$$\kappa$$$ is the thermal conductivity (W/m/K). Using a least-squares algorithm the equation above can be evaluated numerically and both absorption coefficient and thermal diffusion coefficient can be measured experimentally. By varying $$$\alpha$$$ and fitting the equation to the experimental data both $$$\alpha$$$ and $$$D$$$ converge to the correct values. The estimate of $$$\alpha$$$ and $$$D$$$ depend on each other but a high degree of fitting to the experimental data results in correct estimates for both. A plot of $$$d=\sqrt {Dt}$$$ vs. $$$\sqrt{t}$$$ yields a straight line with a slope of $$$\sqrt{D}$$$, the square root of thermal diffusion coefficient as shown in Figure 3. The top two plots are from the MRI data and the bottom plot is from the TCA data. The temporal resolution increases from top to the bottom in the plots as 25, 11.5 and 1 s, respectively. The results from different experiments agree well with the literature data. The absorption coefficient value of 0.6 cm-1resulted in good fitting for the thermal diffusion coefficients ($$$D$$$) as 1.36, 1.31 and 1.35 × 10-7 m2/s in all three experiments, respectively Also, using a value of $$$D$$$, the $$$\alpha$$$ can be probed with higher precision. This study shows that MRI may be used to experimentally measure both RF absorption and thermal diffusion coefficients in the tissues noninvasively.
Acknowledgements
This work was supported and was also performed at the Zuckerman Mind Brain Behavior Institute MRI Platform, a shared resource, and Columbia MR Research Center.References
Figures

A 1.9 GHz half wavelength (λ/2) dipole antenna (left) and a 1.9 GHz rectangular waveguide (WR-430) RF source (right) placed against the ex vivo bovine brain tissue in the cubical plastic containers.
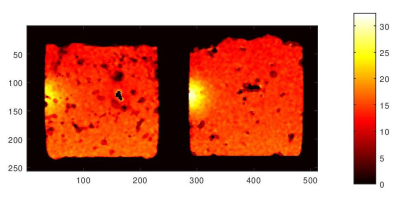
MRI temperature maps of ex vivo brain tissue exposed to a 1.9 GHz half wavelength (λ/2) dipole antenna placed on the left side of the container. The hot spots correspond to RF exposures of 12 minutes time and 2W power. These two images are from two different ex vivo brain tissues and experiments.
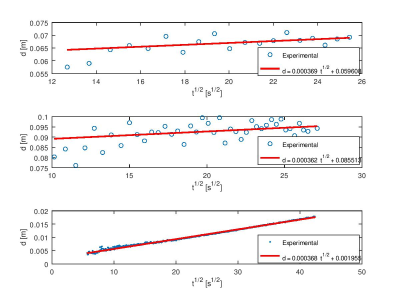
A plot of d=(Dt)1/2 vs. t1/2 yields a straight line with a slope of (D)1/2, the square root of the thermal diffusion coefficient. The top two graphs are from the MRI data and the bottom graph is from the TCA data. The temporal resolution increases from top to the bottom in the plots as 25, 11.5 and 1 s, respectively.