1725
Subsampling Diffusion Gradients via Poisson Sphere Elimination1Biomedical Research Imaging Center, University of North Carolina, Chapel Hill, Chapel Hill, NC, United States
Synopsis
Subsampling from a set of diffusion gradient directions is useful for evaluation of image acquisition and reconstruction strategies. However, a challenge associated with gradient subsampling is the requirement to ensure uniform distribution of a predetermined number of subsampled directions. Here, we introduce a method for near-uniform subsampling for an arbitrary target number of gradient directions.
Introduction
Gradient subsampling requires the outcome to be ideally uniformly distributed for a target number of directions. Few methods have been proposed to tackle this problem. One approach is to select the gradient directions for each shell based on a smaller set of reference directions that are uniformly distributed [1]. Another approach is to split a set of directions into subsets that are approximately uniformly distributed via iterative permutations [2]. However, it is not straightforward using this method to choose a target number of output directions. In this work, we introduce a method for fast subsampling with an arbitrary target number of gradient directions without the need for reference directions or iterative optimization.Methods
We employ Poisson sphere sample elimination [3] for gradient subsampling.Single-Shell Subsampling: With a desired Poisson sphere radius, a dart-throwing mechanism is used to determine whether each sample, in the order of increasing index [4], should be accepted or eliminated based on its distance to previously accepted samples. When two samples are close together, dart-throwing eliminates the sample with the greater index. Hence, given a set of samples in a particular order, dart-throwing picks a subset with an arbitrary size. To avoid explicitly specifying the Poisson sphere radius, we employ a greedy sample elimination algorithm [3] to compute a weight for each sample in a given set and then eliminate the samples with weights greater than a threshold.
Multi-Shell Subsampling: We extend the above method to multi-shell subsampling with an arbitrary target number of gradient directions for each shell. For each sample in a shell, we can compute an intra-shell distance between the sample and the other samples in the same shell, and an inter-shell distance between the sample and the other samples in all shells collapsed into a single shell. We use a weighted combination of the two distances to select samples via Poisson sphere sample elimination. The optimal weight for distance combination is determined based on the minimum error between the spherical mean images computed with the subsampled directions and the original directions.
Materials
We evaluated our method using adult and neonatal data.Adult: Multi-shell dMRI data from the Human Connectome Project (HCP) [5], with $$$b=500, 1000, 1500, 2000, 2500, 3000 \, s/mm^2$$$, voxel size $$$(1.25 \, mm)^3$$$, 90 non-collinear directions per shell, and 18 non-DW images. The goal is to subsample 30 or 60 gradient directions per shell.
Neonate: Multi-shell dMRI data from the developing Human Connectome Project (dHCP) [6], with four phase-encode directions on four shells with b-values of $$$0~(n=20)$$$, $$$400~(n=64)$$$, $$$1000~(n=88)$$$ and $$$2600~(n=128) \, s/mm^2$$$, voxel size $$$(1.5 mm)^3$$$. The data were corrected for eddy-current distortion, susceptibility distortion, and motion artifacts. The goal is to subsample with factors 0.5X and 0.25X.
Directional uniformity is gauged using the range (max-min) of nearest-neighbor angles between all pairs of directions. A smaller range indicates greater uniformity.
Results
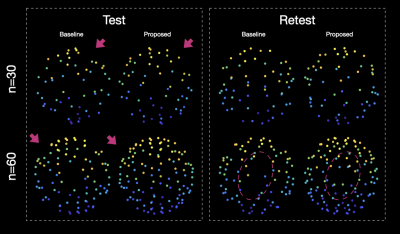
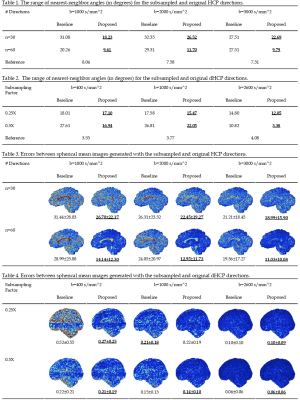
Figure 1 shows the subsampled directions from the HCP gradients (b=1000 s/mm^2, n=90 directions) using a baseline method [1] and the proposed method. One can appreciate that the proposed method results in a more uniform distribution of directions.Tables 1-2 show the ranges of the nearest-neighbor angles [2] of the subsampled samples and the original samples. A smaller range implies a more uniform distribution.
Tables 3-4 show the error maps of the spherical mean images computed with the subsampled directions and the original directions. The smaller errors, measured using absolute mean value of error maps, indicate that our method results in greater uniformity distribution compared with the baseline method.
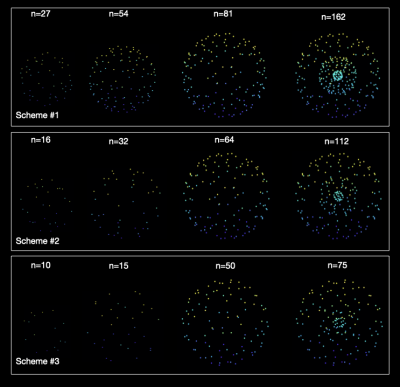
Figure 2 shows the multi-shell directions subsampled from the HCP directions using the proposed method for three different sampling schemes.
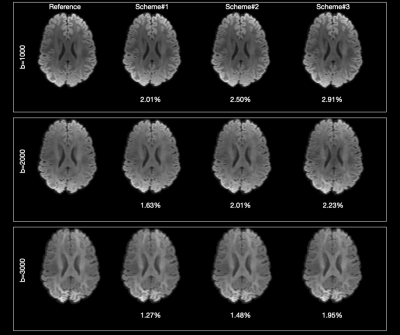
Figure 3 confirms that the subsampled directions given by our method generate spherical mean images that are highly consistent with those generated using the original directions.
Conclusion
We presented a method for fast and effective subsampling of gradient directions. We validated the effectiveness of our method using adult and neonatal diffusion data.Acknowledgements
This work was supported in part by NIH grant NS093842.References
[1].Ye C, Li X, Chen J. A deep network for tissue microstructure estimation using modified LSTM units. Med Image Anal. 2019;55: 49–64.
[2].Tournier J-D, Smith R, Raffelt D, Tabbara R, Dhollander T, Pietsch M, et al. MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. Neuroimage. 2019;202: 116137.
[3].Yuksel C. Sample Elimination for Generating Poisson Disk Sample Sets. Comput Graph Forum. 2015;34: 25–32.
[4].Bridson R. Fast Poisson disk sampling in arbitrary dimensions. SIGGRAPH sketches. 2007;10: 1.
[5].Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, et al. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage. 2013;80: 125–143.
[6].Makropoulos A, Robinson EC, Schuh A, Wright R, Fitzgibbon S, Bozek J, et al. The developing human connectome project: A minimal processing pipeline for neonatal cortical surface reconstruction. Neuroimage. 2018;173: 88–112.
[7].Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42: 515–525.
Figures