Purpose

In physiological and pathological conditions in which multiple underlying tissue properties are expected to vary the diffusion weighted image (DWI) signal, the diagnostic value of conventional apparent diffusion coefficient (ADC) notably decreases. We developed a multimodal apparent diffusion model with four stretch exponential modes to comprehensively describe four separate apparent diffusivity distributions, including flow with D >> 3 µm²/ms, and, unimpeded diffusion with D ≈ 3 µm²/ms, hindered diffusion with 0.1 µm²/ms < D < 3 µm²/ms, and restricted diffusion with D << 0.1 µm²/ms. In this preliminary study, we demonstrate the refined precision of the hindered diffusion mode within gray and white matter.

Methods and Materials

Under an approved IRB protocol, full spectrum of diffusion weighted images were acquired from healthy subjects (n=4) using 22 b‑values from 0 to 5000 s/mm² in 7 minutes, on a 3T MRI scanner (GE MR750). In this study, DWI data was modeled voxel-wise as a sum of four stretch exponential[1-3] modes: flow (f_F, D_F, α_F=1), unimpeded (f_UI, D_UI=3 µm²/ms, α_UI=1), hindered (f_H, D_H, α_H), and restricted (f_R, D_R = 0.0001 µm²/ms, α_R=1), where f_x is the fraction of voxel attenuation explained by mode x, D_x is the diffusivity, and α_x is the distribution shape narrowness (from 0.5 – uniform distribution, to 1 – delta function, i.e., monoexponential). Parameters that could not be determined empirically were fixed as specified. Regression of diffusion weighted MRI voxel signal was performed using successive linearized fitting using a Theil-Sen linear regressor (which is resilient up to 29.3% outliers)[4-5] , thusly, the stretch exponential,
$${S_b}/{S_0}=e^{-(b \cdot {D_x})^{\alpha_x}}$$
was be linearized to,
$$\ln(-ln({S_b}/{S_0}))={\alpha_x}ln{b}+{\alpha_x}ln{D_x} $$
and given these two postulates ( $$$\mu_N$$$ – noise floor),
$$ln({f_1}e^{-(b \cdot {D_1})^{\alpha_1}} + {f_2}e^{-(b \cdot {D_2})^{\alpha_2}} ) \simeq{\alpha_3}ln{b} + {\alpha_3}ln{D_3} \;:\;{D_2} \ll {D_1} \;and\; {f_1}e^{-(b \cdot {D_1})^{\alpha_1}}, {f_2}e^{-(b \cdot {D_2})^{\alpha_2}} \gg {\mu_N}$$
and,
$$ln({f_1}e^{-(b \cdot {D_1})^{\alpha_1}} + {f_2}e^{-(b \cdot {D_2})^{\alpha_2}} ) \simeq ln {f_2} - b \cdot {D_2} \;:\;{D_2} \ll {D_1} \;and\; {f_1}e^{-b \cdot {D_1}} \ll {\mu_N}\;and\;{f_2}e^{-b \cdot {D_2}} \gg {\mu_N}$$
each voxel’s linearized diffusion signal can be examined for the deviations from linearity and thus ranges of b-values selected for each apparent diffusion mode. Note that there were no recognized means during regression to correct and/or compensate for corruption due to pulsatile flow, especially at b = 0⁺ s/mm². These voxels are identified using a Pearson correlation coefficient r_xy⁠, within the range 0⁺ to 150 s/mm², where -1 is perfectly valid and +1 is perfectly invalid, and herein referred to as low b bad.

Results

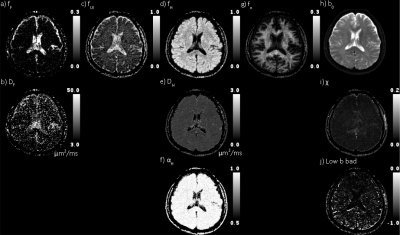
A Monte Carlo simulation was performed to evaluate the fitting accuracy of the quad modal model’s parameters, as demonstrated in Figure 1, and it depicted some trade offs in the fitting accuracy of the parameters. First, the inaccuracy of the modes’ fraction follows the successive order of fitting, i.e., R, H, UI, F; see Figure 1. Even though closest to the noise floor, the restricted fraction is regressed with relatively high accuracy. Second, there is a trade off between large D_H and a large f_UI. And third, the accuracy of the hindered shape parameter is proportional to α_H. As expected, increasing the images’ SNR increases the regression’s accuracy.

For evaluation of the proposed quad-modal model in a healthy adult brain, see Figure 2. Appreciate the correspondences to fundamental physiological properties, f_F to communicating CSF, f_UI to CSF, f_H>0.8 to cortical GM, and f_R>0.1 to WM. The χ map lacks an apparent correspondence to anatomy, except for fluid-tissue boundaries. The undulation at luminal surfaces may explain elevated residuals at these locations. There appears to be an inverse correlation in the A/P direction between the low b bad map and the subarachnoid CSF.

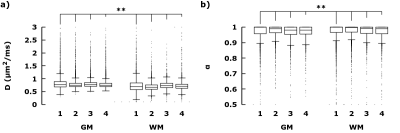
With the elimination of the flow, unrestricted, and highly restricted diffusion components, the distribution of hindered diffusitivities, across the presented healthy brain slice, have been centered (D_H at 0.735±0.25 μm²/ms) and narrowed (α_H at 0.96±0.06) (μ±σ). The distributions of D_H and α_H within cortical GM (f_H > 0.8) were observed at 0.757±0.091 μm²/ms and 0.972±0.033, respectively; and within WM (f_R > 0.1) at 0.706±0.124 μm²/ms and 0.978±0.0326, respectively. Both D_H and α_H between GM and WM differ significantly (p<0.01 , Student t-test). See figure 3 for comparison across four healthy subjects.

Conclusion

With accurate and comprehensive fitting of the distributions of apparent diffusion for GM and WM, MAD MRI may be utilized for comprehensively study microstructural changes of brain under healthy and pathological conditions.

Acknowledgements

The work is partly supported by University of Illinois at Chicago Radiology departmental research funds and the National Institutes of Health [R21EB023516, R21AG053876, and R01AG061114].