Introduction

Diffusion tensor imaging (DTI) typically involves decomposing the tensor into its eigenvalues and computing mean diffusivity (MD) and fractional anisotropy (FA). DTI studies have consistently detected increased MD and decreased FA with advancing age in lateral regions of primarily single white matter (WM) fibre bundles, but findings have been inconsistent in medial regions of more complex fibre architecture. FA exhibits weak sensitivity to age in the corona radiata and internal capsule, and recent DTI studies with larger samples have found sporadic increases in FA with age, likely resulting from selective degeneration of secondary crossing fibres.^1-2 The lack of more consistent detection of these increases in FA with age can be attributed to FA and MD not being mutually orthogonal,³ that is, increased MD with age masking increases in tensor anisotropy with age.

Given that DTI remains more common for characterizing aging WM than advanced diffusion MRI models due to DTI’s simplicity, robustness and efficiency, it is critical to strive to maximize the information extracted from DTI across the entire WM, including regions of complex fibre architecture. Therefore, rather than stopping short at two non-orthogonal metrics of MD and FA, and rather than employing the eigenvalues directly, which do not provide a holistic representation of tensor shape, the present study employs a complete trivariate orthogonal decomposition of the tensor based on its eigenvalue moments.

Methods

Study Participants
All subjects were participants of the UK Biobank.¹ Subjects were excluded from our study if they reported a neurological, psychological or psychiatric disorder, neurological injury, or history of stroke. Subjects were then divided up into seven age categories of [46-50, 51-55, 56-60, 61-65, 66-70, 71-75, 76-80] years, and 50 male and 50 female subjects were randomly selected from each of the seven age categories. The final sample thus consisted of 700 subjects aged 46-80 (50% male, 50% female).

Diffusion MRI Data
Diffusion MRI data were acquired as part of the UK Biobank on a Siemens Skyra 3T system with 5 b=0, 50 b=1000s/mm² and 50 b=2000s/mm² volumes (100 distinct directions) at TR = 3.6s, TE=92ms, matrix size=104x104x72 with (2mm)³ resolution, 6/8 partial Fourier, 3x multislice acceleration and no in-plane acceleration. An additional 3 b=0 volumes were acquired with a reversed phase encoding. The data were corrected for eddy-current and susceptibility-related distortions via EDDY⁴ and TOPUP,⁵ respectively.

Data Processing
The diffusion tensor was computed voxelwise by fitting the diffusion MRI signal from the b=0 and b=1000s/mm² shells to the DTI model. Three orthogonal DTI metrics {mean diffusivity (MD), norm of anisotropy (NA), mode of anisotropy (MO)} were computed based on the moments of the tensor’s eigenvalues {λ₁,λ₂,λ₃} via³

MD = (λ₁ + λ₂ + λ₃)/3

NA = √[(λ₁-MD)² + (λ₂-MD)² + (λ₃-MD)²]

MO = 3√6 [(λ₁-MD)(λ₂-MD)(λ₃-MD)]/NA³

To interpret age associations of these metrics in complex fibre architecture, BEDPOSTX was applied to the b=0, b=1000 and b=2000 s/mm² shells to estimate the proportion of each crossing tract per voxel.⁶

Statistical Analysis
FSL’s Tract-Based Spatial Statistics (TBSS) was used to obtain a WM skeleton.⁷ For voxelwise analysis, a relationship of metric with age defined by p<0.05 with correction for multiple comparisons (cluster-wise controlling family-wise error rate with 5000 permutations) and controlling for gender as per FSL’s randomise.⁸ Age-related difference of metric per year was calculated using a general linear model as implemented in FreeSurfer.⁹

Results

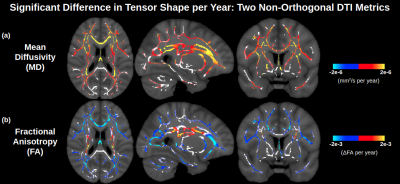
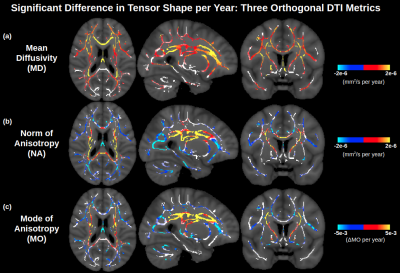
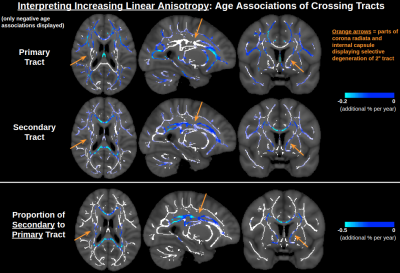
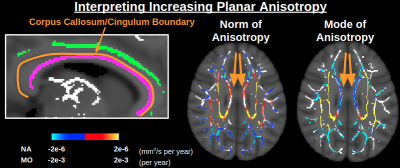
Figure 1 displays significant age associations of the conventional (non-orthogonal) DTI metrics MD and FA. FA is generally insensitive to age in medial regions, other than some sporadic positive age associations of FA. In Figure 2, it is seen that the orthogonal decomposition yields clear and consistent positive age associations of NA throughout these medial regions. In conjunction with MO, the orthogonal decomposition reveals increased linear anisotropy with advancing age in the corona radiata, internal capsule and corpus callosum splenium, and increasing planar anisotropy with advancing age in the corpus callosum body. When comparing with BEDPOSTX fibre-fraction outputs, increasing linear anisotropy can be interpreted as selective degeneration of secondary crossing fibres (anterior-posterior association fibres) while the principal fibres (superior-inferior projection fibres) remain relatively intact (Figure 3), and increasing planar anisotropy can be interpreted as degeneration of callosal fibres alongside decreased partial-voluming with cingulum fibres (Figure 4).

Discussion and Conclusion

Use of an orthogonal moment tensor decomposition revealed positive age associations of anisotropy in regions of complex fibre architecture that exhibited limited age associations of FA. Specifically, while FA demonstrates low sensitivity to age in the corona radiata, internal capsule and posterior corpus callosum, NA and MO are consistently sensitive to age throughout these regions, indicating that the previous challenges of DTI in these regions were due to the choice of decomposition rather than the DTI model itself. Therefore, this study demonstrates that if an advanced diffusion MRI technique is not feasible, the conventional DTI model can still be used to gain insight into crossing fibre regions by using the orthogonal moment decomposition, bearing in mind that the complex fibre architecture of WM tissue means that degeneration does not always manifest itself as decreases in tensor anisotropy.

Acknowledgements

This research has been conducted using the UK Biobank Resource under Application Number 40922. We thank CIHR, NSERC and NIH for financial support.