Purpose

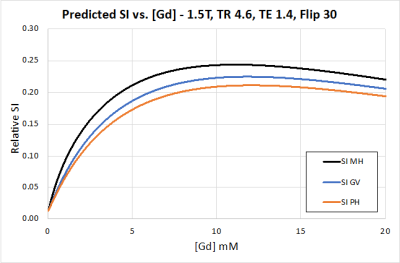
Recent in vitro work has demonstrated a sublinear relationship between gadolinium-based contrast agent blood concentration [GBCA] and R₁, and a potentially impactful increase in R₂* values at first-pass arterial concentrations.^1,2 This is due to water exchange across the red blood cell (RBC) membrane and the effects of excluding gadolinium from ellipsoid RBCs. Thus, as [GBCA] increases, arterial signal intensity (SI) for a gradient echo sequence is expected to rise, plateau, and then diminish (Figure 1). This suggests that for contrast enhanced MR angiography (CE-MRA), increasing [GBCA] by injecting more quickly will not necessarily increase SI, but instead the faster injection rate will shorten bolus duration with resultant image blurring and degradation.³ While theoretically sound, there does not exist a validated model using these constructs whereby CE-MRA signal intensity can be accurately predicted based on in vivo [GBCA].^1,2 We seek to establish such a model based on the in vivo behavior of multiple GBCAs in pigs.

Methods

We investigated six juvenile German swine (53-63 kg). Under general anesthesia, two animals each were administered three separate 0.1 mmol/kg doses of one of three GBCAs: gadoteridol (ProHance, Bracco), gadobenate (MultiHance, Bracco), gadobutrol (Gadavist, Bayer). All injections were performed in randomized-order at varying rates (1, 2, or 3 mL/s) during time-resolved 3D SPGR imaging of the aorta (1.5T Siemens Aera, TR/TE 4.6/1.4 ms, α=30^o, temp res 1.7 s). Concurrently, 0.5 mL aliquots of arterial blood were sampled every 2 seconds x 40 by aortic catheter and sent for mass spectrometry to determine [GBCA]. These data were used to predict blood SI using the SI equation for SPGR imaging:

$$$\space\space\space\space\space\space\space\space$$$ [1] $$$\space\space\space\space\space\space\space\space$$$ $$$\space\space\space\space\space\space\space\space$$$ $$$SI_{SPGR}\space\alpha\frac{1-e^{-TR·R_{1}}}{1-\cos(\alpha·e^{-TR·R_{1}})}\sin(\alpha)·e^{-TE·R_{2}^{*}}$$$


where R₁ is the GBCA dependent T₁ relaxation rate in blood (i.e. R_1blood), which can be calculated per ¹ as:

$$$\space\space\space\space\space\space\space\space$$$ [2] $$$\space\space\space\space\space\space\space\space$$$ $$$\space\space\space\space\space\space\space\space$$$ $$$R_{1blood}=\frac{1}{2}[R_{1i}+R_{1p}+\frac{1}{\tau_{i}}+\frac{1}{\tau_{o}}]$$$ $$$-\frac{1}{2}\{[(R_{1i}-R_{1p})+(\frac{1}{\tau_{i}}-\frac{1}{\tau_{o}})]^{2}$$$ $$$+\frac{4}{\tau_{i}\tau_{o}}$$$ $$$\}^{\frac{1}{2}}$$$

where R_1i is the fixed T₁ relaxation rate inside the RBC (assumed 0.8/s at 1.5T), τ_1i and τ_1o represent average water residence times inside and outside the RBC, with τ_1i established 5 ms, and by mass conservation $$$\tau_{1o}=\tau_{1i}(\frac{1-Hct}{Hct})$$$. R_1p is the GBCA dependent T₁ relaxation rate in plasma:

$$$\space\space\space\space\space\space\space\space$$$ [3] $$$\space\space\space\space\space\space\space\space$$$ $$$\space\space\space\space\space\space\space\space$$$ $$$R_{1p}=R_{1o}+r_{1f}[CR]+r_{1b}[CRM]$$$

where R_1o is the T₁ relaxation rate outside the RBC without GBCA (0.8/s at 1.5T), [CR] = concentration unbound GBCA and [CRM] = concentration of bound Macromolecule-GBCA. [CR] (for gadobenate) can be determined from the protein binding coefficient K_b.¹ r_1f and r_1b are the plasma relaxivities of free and bound GBCA respectively. R₂*_blood is the GBCA dependent T₂* relaxation rate in blood²:

$$$\space\space\space\space\space\space\space\space$$$ [4] $$$\space\space\space\space\space\space\space\space$$$ $$$\space\space\space\space\space\space\space\space$$$ $$$R_{2}$$$*$$$_{blood}=R_{2}$$$*$$$_{o}+r_{2}$$$*$$$[CR_{T}]$$$

R₂*_o represents the fixed T₂* relaxation rate outside the RBC in the absence of GBCA (5 ms at 1.5T) and r₂* is the T₂* relaxivity of GBCA in blood.² Total GBCA [CR_T] = [CRM] + [CR].

Hematocrit and [albumin] were measured per pig. Relaxivities r_1f, r_1b, r₂* and protein binding constant K_b were calculated per Wilson et al.^1,2 Using these data in conjunction with [1-4], predictive modeling of SI vs. time was made for each of the 18 injections for which [GBCA] vs. time was known. Modeling was also performed neglecting R₁ effects (i.e. assuming R₁ behaves as if in plasma), and neglecting R₁ and R₂* effects (i.e. additional assumption R₂* effects unimportant). Relative gain between MRA and predictive data was adjusted to each animal’s first injection baseline and held constant for the subsequent two injections. Predicted and observed SI were compared using mean absolute error (MAE), mean square error (MSE), and visual analysis.

Results

The r_1f and r₂* values for all agents, as well as protein binding coefficient K_b for gadobenate, were near identical to human values (gadoteridol 3.8 s^-1/mM, 22 s^-1/mM, n/a; gadobutrol 4.3 s^-1/mM, 21 s^-1/mM, n/a; gadobenate 5.1 s^-1/mM, 20 s^-1/mM, 1.5 mM^-1 respectively). The measured r_1b value for gadobenate was lower in pigs than humans (9.1 vs. 18.1 s^-1/mM).

Figure 1 illustrates the expected rise, plateau, and decrease in expected SI vs. [GBCA] for all three agents based on [1-4] above. Comparing predicted vs. measured SI for each across three consecutive injections for three agents revealed high correlation when fully accounting for blood R₁ and R₂* effects (Figures 2-4), average MAE 7.6, MSE 40. Each subsequent baseline over the three consecutive GBCA injections was well predicted with a single gain constant per animal. The models neglecting blood R₁, or both R₁ and R₂* effects show decreased accuracy (Figure 5), with MAE and MSE increasing to average 560 and 12,765 respectively.

Discussion

The sublinear behavior of R₁ and the high first-pass R₂* values in blood as described by Wilson et al. are supported in an animal model, thus validating this work in vivo. If these effects are neglected, the predictive model of SI decreases in accuracy relative to the observed SI. By characterizing and understanding the effects of R₁ and R₂* as applied to first-pass CE-MRA, we present a method of more accurately predicting actual signal intensity for any given blood [GBCA], a critical factor to understand and optimize the relationship between blood [GBCA] and achieved signal intensity. This model can be used to improve image quality, as well as potentially reduce contrast usage and cost.

Acknowledgements

No acknowledgement found.