1602
Decomposition of the incomplete volume-surface integral equation matrices for MR coil simulations1Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 2Department of Electrical & Computer Engineering, Massachusetts Institute of Technology, Cambridge, MA, United States, 3The Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 4Vilcek Institute of Graduate Biomedical Sciences, New York University Grossman School of Medicine, New York, NY, United States
Synopsis
The volume-surface integral equation (VSIE) method is used for rapid and accurate simulations of electromagnetic fields in magnetic resonance imaging. For the case of a 7T array and a numerical head phantom, we constructed the VSIE coupling matrix that models the interactions between the coil and the scatterer. We reshaped the columns of the matrix as incomplete 3D tensors. We investigated how the low rank properties of these tensors, could be exploited to compress the coupling matrix, by expressing the tensors in their canonical form. We showed that an excellent compression could be achieved with an error lower than 2%.
Introduction
A plethora of computational electromagnetics (EM) algorithms have been proposed for fast and accurate magnetic resonance (MR) simulations. For example, tensor decompositions were introduced to reduce the memory footprint of the Green function operators in volume integral equation based approaches1. Such operators are purely geometrical and do not depend on the object’s electrical properties, therefore they can be assembled once, stored, and re-used in future EM simulations2. However, they require an overwhelming amount of memory for the case of fine voxel resolutions (2 mm or less), and, storing them in their full form is inefficient and impractical. This can be addressed with tensor decompositions, which enables storing the mentioned operators in compressed forms, while at the same time they facilitate executing the associated EM simulations on GPUs with limited memory. In this work, we propose a technique to compress the volume-surface integral equation (VSIE) coupling matrix, which corresponds to the Green’s function operator that models interactions between radiofrequency coils and the sample. We exploit the fact that this matrix is incomplete, because interactions with “air” voxels in the domain are not computed; therefore, it can be compressed via an optimization routine.Theory and Methods
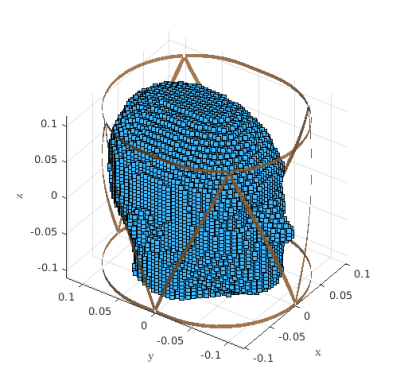
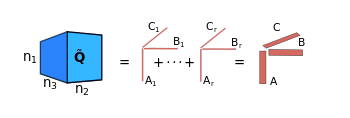
We loaded an 8-element array3 (Figure 1) with the “Duke” head4 and set the operating frequency to 298 MHz (7 Tesla MR imaging). We used a uniform voxelized simulation domain ($$$19 \times 23.5 \times 23$$$ cm$$$^3$$$) with 5 mm isotropic resolution. The coil was discretized with a triangular tessellation (528 non-boundary edges). We used MARIE2 to model the coupling matrix between the array and the head (coils’ electric currents to head’s magnetic fields). The head and array were modeled with piecewise constant and RWG basis functions, respectively. We generated 2 coupling matrices: a full matrix (246468 x 528 elements, required memory = 1,900 MB), modeling interactions between the array and all voxels of the domain, and an incomplete matrix (109989 x 528 elements, required memory = 865 MB), considering only the voxels of the head. Both matrices’ columns were reshaped into tensors, and compressed independently with the canonical polyadic decomposition5 (CPD). The low multilinear rank approximation of the tensors was performed with the quasi-Newton methods of Tensorlab6, which employs for full tensors the methods presented in7 and for incomplete, the ones in8. In total, 1584 tensors of dimensions $$$38 \times 47 \times 46$$$ were compressed for each matrix. CPD is unique, under mild conditions, and approximates the initial tensor with a sum of r rank-1 tensors (Figure 2). r is called the canonical rank.Results
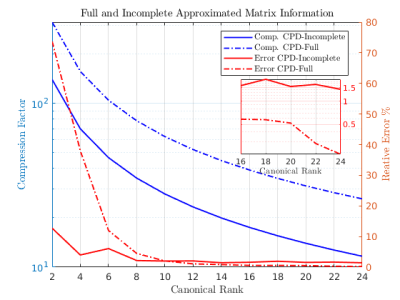
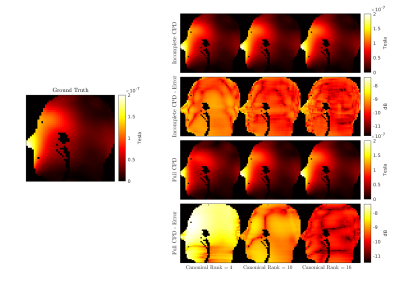
We performed the compression of the full and incomplete VSIE coupling matrix for 12 canonical ranks (2, 4, …, 22, 24). We computed CPD within a 1000-iterations quasi-Newton nonlinear least-squares-based optimization algorithm. For the incomplete matrix, for a few ($$$ \leq 2$$$) columns and canonical ranks $$$> 4$$$, the CPD algorithm was ill-posed and the approximation of the tensors failed. For these cases, we replaced the approximation of such columns with the corresponding approximation successfully computed for lower ranks. Figure 3 displays the relative error over all matrix columns after the compression with CPD, showing that for the case of the full matrix and low canonical ranks, the decompressed matrix was not accurate. However, for canonical ranks >= 10, the error was $$$< 1\%$$$. In the incomplete case, the error was small for all canonical ranks, but never lower than $$$1.5\%$$$. The overall matrix compression factor remained between 26 and 313, and 11 and 140 for the full and incomplete matrix, respectively. The latter had a smaller compression factor, because it considers only voxels in the head. For both cases, the memory footprint of the compressed matrices was between 6 and 76 MB depending on the canonical rank. Figure 4 shows a qualitative comparison of the two cases for a central sagittal section and three representative canonical ranks (4,10,16). The reconstructed tensors in the incomplete case resembled the ground truth for all chosen ranks. For the full matrix case, the reconstruction was not accurate for canonical rank = 4, but was successful for the higher ranks.Discussion and Conclusions
Here we introduced a method (the first one in authors’ knowledge) to compress an incomplete version of such a matrix, by exploiting its low-rank properties. As a result, a compression factor of 35 could be achieved with $$$< 2\%$$$ error and without assembling the full matrix, which is not always feasible, due to memory requirements. Our approach could prove useful for compression and storage of scatterer-specific EM bases, where only the interactions with the scatterer’s voxels are modeled9. Due to the complexity of the CPD optimization algorithms, the proposed approximation of incomplete tensors is slow, since multiple tensors need to be compressed. However, since each tensor component is compressed independently, the computation can be efficiently parallelized. Furthermore, the low memory cost can enable the use of heterogeneous computing techniques1 to accelerate EM simulations and possibly approach the performance of other techniques, such as the precorrected fast Fourier transform method10, in MRI applications.Acknowledgements
This work was supported by NIH R01 EB024536 and by NSF 1453675. It was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).References
[1] Giannakopoulos, Ilias I., Mikhail S. Litsarev, and Athanasios G. Polimeridis. "Memory footprint reduction for the FFT-based volume integral equation method via tensor decompositions." IEEE Transactions on Antennas and Propagation 67.12 (2019): 7476-7486.
[2] Villena, Jorge Fernández, et al. "Fast electromagnetic analysis of MRI transmit RF coils based on accelerated integral equation methods." IEEE Transactions on Biomedical Engineering 63.11 (2016): 2250-2261.
[3] Giannakopoulos, Ilias, et al. "Magnetic-resonance-based electrical property mapping using Global Maxwell Tomography with an 8-channel head coil at 7 Tesla: a simulation study." IEEE Transactions on Biomedical Engineering (2020).
[4] Christ, Andreas, et al. "The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations." Physics in Medicine & Biology 55.2 (2009): N23.
[5] Hitchcock, Frank L. "The expression of a tensor or a polyadic as a sum of products." Journal of Mathematics and Physics 6.1-4 (1927): 164-189.
[6] Vervliet, Nico, Otto Debals, and Lieven De Lathauwer. "Tensorlab 3.0—Numerical optimization strategies for large-scale constrained and coupled matrix/tensor factorization." 2016 50th Asilomar Conference on Signals, Systems and Computers. IEEE, 2016.
[7] Sorber, Laurent, Marc Van Barel, and Lieven De Lathauwer. "Optimization-based algorithms for tensor decompositions: Canonical polyadic decomposition, decomposition in rank-(Lr,Lr,1) terms, and a new generalization." SIAM Journal on Optimization 23.2 (2013): 695-720.
[8] Vervliet, Nico, et al. "Breaking the curse of dimensionality using decompositions of incomplete tensors: Tensor-based scientific computing in big data analysis." IEEE Signal Processing Magazine 31.5 (2014): 71-79.
[9] I. P. Georgakis, et al, “Consistent numerical basis of electromagnetic fields in realistic human body models for MRI system design and optimization,” in International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 2017, p. 1063.
[10] Guryev, G. D., et al. "Fast field analysis for complex coils and metal implants in MARIE 2.0." in Proc. ISMRM, 2019, p. 1035.
Figures