Introduction

Previous work with MR fingerprinting (MRF) has demonstrated the ability to acquire 3D quantitative parameters, mainly with the use of 2D spirals rearranged in 3D k-space^1-6. Recent work by Speidel et al.⁷ has demonstrated the use of Seiffert spirals for efficient acquisition of 3D k-space. By utilizing these 3D trajectories, we hypothesize that 3D MRF acquisitions can be designed for more time-efficient acquisition compared to conventional techniques. In this study, we evaluate the use of seiffert spirals for the acquisition of T₁ and T₂ relaxation times using MRF techniques.

Methods

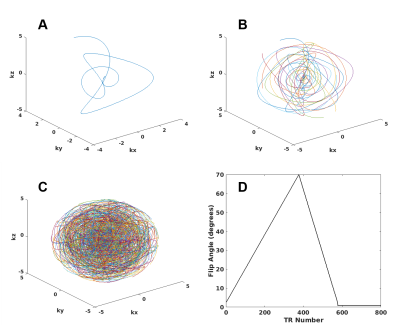
Seiffert spiral design: Similar to Speidel et al., a seiffert spiral was calculated using equation 1, where sn and cn are Jacobi’s elliptical functions and m determines the velocity of the spiral. For our implementation, a longer seiffert spiral was generated and then separated into 8 individual spirals (m=0.15) with a 4.51ms readout duration and isotropic resolution. All eight spirals are shown in Figure 1a and 1b. These 8 spirals were acquired consecutively every 8 TRs, and then rotated around the origin by the golden angle. For all acquisitions/simulations in this study, 12,000 TRs were acquired for a total of 1,500 rotations. A sampling of every 100 rotated spirals is shown in Figure 1c. To induce signal changes, flip angle variations (shown in Figure 1d) are repeated every 800 TRs, for a total of 15 repetitions, similar to the work of Gomez, et al.¹. Before each repetition, an adiabatic inversion pulse was applied to induce T₁ recovery.
$$ρ = sn(s|m), z = cn(s|m), Φ = κs, κ=√m$$
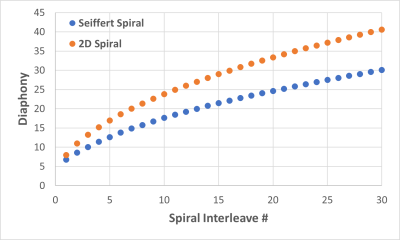
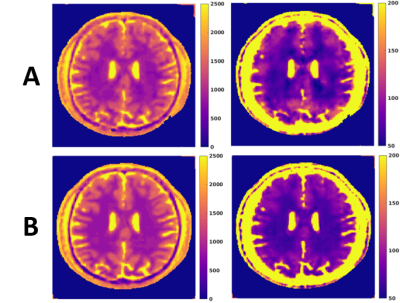
Simulation Comparison: To determine sampling efficiency, the diaphony⁸ of 40 interleaves was compared between the proposed sequence and a 2D spiral with the same resolution, acquisition time, and rotations as the seiffert spiral acquisition. Additionally, simulated brain data was created using high resolution brain segmentations obtained from the Brainweb project⁹. For each tissue (gray matter, etc.), simulated signal curves were generated using Bloch equations and then sampled in k-space by the two trajectories. The simulated k-space data for both trajectories was then reconstructed using a subspace constrained FISTA reconstruction in the Berkeley Advanced Reconstruction Toolbox¹⁰. A dictionary was simulated using Bloch equations with 69 T₁ values from [100:50:3000,3200:200:5000] and 64 T₂ values from [3:3:150,175:25:500] over 12,000 TRs. The reconstructed subspace images were then fit for T₁ and T₂ values using the dictionaries entries with the highest inner product and compared to the true T₁ and T₂ brain images using normalized root mean square error (NRMSE).
Phantom Validation: To demonstrate the feasibility of the proposed technique, agarose phantoms of various concentrations were scanned with the proposed test sequence. Sixteen phantoms (1/2/3/4% agarose with 2/6/12/20mg/kg of ferumoytol) were scanned in a 20-channel head coil on a Siemens 3T Prisma system. Conventional T₁ images were acquired with a variable flip angle VIBE sequence and conventional T₂ images were acquired with a multi-echo spin echo sequence. The proposed 3D MRF sequence acquired and reconstructed as described previously. Mean values were obtained using the center 3x3 section of each phantom and ICC values were calculated between the 3D MRF and conventional sequences.
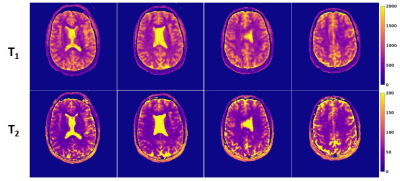
In Vivo: Lastly, to demonstrate in vivo feasibility, a healthy volunteer (28 year old male) was recruited under an OHSU IRB approved protocol and scanned on a 3T Siemens Prisma scanner with a 20-channel head coil. The proposed 3D MRF sequence was then acquired in the head of the volunteer and T₁/T₂ relaxation maps were reconstructed.

Results

The diaphony of the two sampling schemes are shown in Figure 2, showing decreased diaphony for the proposed seiffert sequence. Example images of the simulated data are shown in Figure 3, in which the 2D trajectory had a NRMSE of 21.9 and 12.2 for T₁ and T₂, respectively. For the seiffert spiral trajectory, the NRMSE was 17.9 and 7.6 for T₁ and T₂, demonstrating approximately 40% improvement in the error. For the phantom validation, the ICC values between the 3D MRF and conventional sequences were 0.967 and 0.915 for T₁ and T₂ respectively. The acquired 3D relaxation maps are shown in a few of the slices of the brain in Figure 4, demonstrating good image quality in 3 minutes using a TR=15ms.

Discussion

As seen in the simulation results, the error was substantially lower using the proposed seiffert trajectory compared to the 2D spiral trajectory, suggesting more efficient coverage of k-space. Similarly, the decreased diaphony suggests more evenly distributed 3D k-space acquisition. The phantom experiment demonstrated good agreement between conventional sequences and the proposed 3D MRF sequence. Lastly, the relaxation maps obtained in vivo demonstrate good image quality, especially considering the low scan time. The results in this study demonstrate the effectiveness of the use of seiffert spirals for 3D MRF acquisition, allowing for high resolution acquisition in a short period of time, with less error compared to conventional techniques.

Conclusion

This study demonstrates the ability of seiffert spiral trajectories to efficiently quantify T₁ and T₂ relaxation using MR fingerprinting techniques. Future work will focus on comparing the seiffert and 2D spiral trajectories in vivo, as well as comparing them to conventional relaxometry techniques.

Acknowledgements

Grant Support: This project was supported in part by a training fellowship from the Brenden-Colson Center for Pancreatic Care, NIDDK grant R01DK117459, and a Medical Research Foundation New Investigator grant.