Synopsis

Magnetic resonance fingerprinting (MRF) is an imaging technique that effectively samples the transient state signal to achieve the goal of fast multi-parameter measurement. However, the applications of MRF only focus on static images, mostly brain image. Therefore, this study aims to investigate the feasibility of different acquisition schemes of four-dimensional magnetic resonance fingerprinting (4D-MRF) by computer simulation.

Introduction

Recently, quantitative magnetic resonance imaging (MRI) technique has drawn increasing attention including magnetic resonance fingerprinting (MRF),1 magnetic resonance image compilation (MAGIC),2 and magnetic resonance spin tomography in time-domain (MR-STAT).3 Among these quantitative techniques, MRF has been investigated intensively since its first introduction in 2013.1 It is an imaging technique that effectively samples the transient state signal to achieve the goal of fast multi-parameter measurement. However, the applications of MRF only focus on static images, mostly brain image. Therefore, this study aims to investigate the feasibility and different acquisition methods of four-dimensional magnetic resonance fingerprinting (4D-MRF) by computer simulation.

Method

The simulation of MRF data acquisition and reconstruction were performed in Matlab (MathWorks, Natick, MA) using in-house developed programs. The simulated MRF technique consists of a IR-FISP MRF sequence with spiral trajectory acquisition. In total, one thousand time points were simulated with 12 ms TR for dictionary matching. For each slice, phase-sorting method was used to re-bin the acquired data into 10 phases. The 4D-MRF were generated by simulating the images slice by slice and then combined to form 3D volume. In order to study the influence of the number of repetitions used for dictionary matching on the image quality, MRF images were simulated with different number of repetitions from 1 to 15 and the simulation was repeated 200 times for each number of repetitions. Extended cardiac-torso (XCAT) phantom is a highly detailed whole-body numerical phantom and it was used in this study. Abdominal T1, T2, and proton density (PD) maps were generated using the XCAT phantom with irregular breathing patterns for MRF simulation. The maximum diaphragm motion was set to 2 cm in cranial-caudal (CC) direction and 1.2 cm in anterior-posterior (AP) direction. The diameter of the tumor embedded in liver was 30 mm. Voxel size was 1.67 isotropic. Three different methods were used to generate 4D-MRF images: 1) continuous acquisition without delay between MRF repetitions; 2) continuous acquisition with 5 seconds delay between MRF repetitions; 3) triggered acquisition with variable delay between MRF repetitions to allow the next acquisition to start at different respiration phase. After the generation of 4D-MRF images, the image quality indexes, including absolute T1 and T2 value error, signal to noise ratio (SNR), and tumor contrast were used to evaluate the reconstructed images with different repetitions. The absolute T1 and T2 value were compared with the ground truth values from XCAT phantom images.

Results

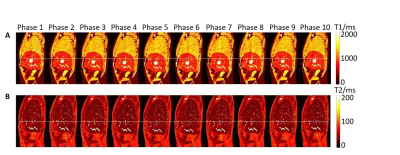
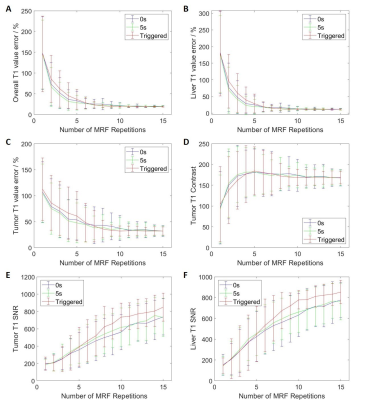
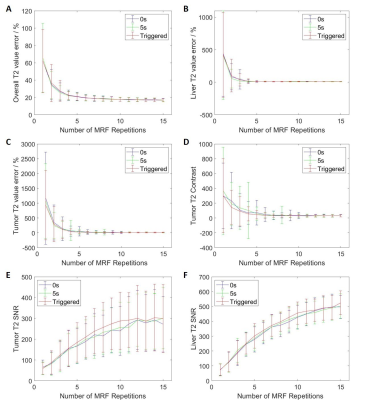
Dynamic MR parametric maps using three different acquisition methods were successfully estimated from both XCAT phantom. An example of simulated 4D-MRF images is shown in Figure 1. The overall and liver T1 value error, liver SNR in T1 and T2 maps, and tumor SNR from T1 maps from triggered method is significantly different compared to the other two methods (p-value < 0.05). The other image quality indexes have no significant difference between the triggered method and the other two fixed-gap methods. All image quality indexes exhibit no significant difference (p-value >0.05) between the acquisition methods with 0 second and 5 seconds delay. The image quality indexes measurement results are shown in Figure 2 to Figure 3.

Discussion

We have successfully demonstrated the feasibility of 4D-MRF technique and investigated three different acquisition methods using computer simulation. Among three different acquisition methods, triggered method showed better performance in terms of certain image quality indexes than the other two methods while the other two methods showed no significant difference between them. However, the 0s gap acquisition method can save around 17 mins for a 20 slices 4D-MRF acquisition compared to the other two methods and the triggered method requires additional manual efforts. Further in vivo studies are needed to determine the optimal acquisition method for clinical practice.

Conclusion

4D-MRF technique was investigated using three different acquisition methods in computer simulation where the triggered method showed better performance than the other two methods. The triggered method has been tested successfully in healthy volunteers.

Summary

We investigated three different acquisition methods for 4D-MRI technique in simulation study.

Acknowledgements

This research was partly supported by research grants (GRF 151022/19M and GRF 151021/18M).