1566
An Efficient Approach to Optimal Design of MR Fingerprinting Experiments with B-Splines1Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin, Austin, TX, United States, 2Department of Biomedical Engineering, The University of Texas at Austin, Austin, TX, United States
Synopsis
Optimal design of acquisition parameters utilizing the Cramer-Rao bound provides improved SNR efficiency for MR fingerprinting experiments. The early work demonstrates that smooth magnetization evolutions resulting from constraining the flip angle variation lead to improved estimation performance. Here we introduce a new formulation, in which we constrain the sequence of acquisition parameters in the low-dimensional spline space. The proposed formulation enforces smooth magnetization evolutions with significantly reduced degrees of freedom. Compared to the state-of-the-art experiment design approach, it improves the computational efficiency by two orders of magnitude, while achieving a similar or slightly better SNR efficiency of the imaging experiments.
Introduction
MR fingerprinting (MRF) is a new paradigm for quantitative MRI1. While the original MRF design uses random or pseudorandom acquisition parameters, optimizing MRF experiments using the Cramer-Rao bound (CRB) provides improved reconstruction/estimation performance2–5 and the CRB-based optimal design features highly-structured acquisition parameters. In the early work, it has also been demonstrated that enforcing smooth magnetization evolutions by constraining flip angle variation is advantageous for the highly-undersampled imaging experiments. However, the state-of-the-art approach with a non-parametric flip angle constraint is computationally intensive. In this work, we reformulate the problem by introducing a parametric representation of the acquisition parameters using B-splines. This low-dimensional representation captures the optimal acquisition parameters while enforcing the smoothness of the magnetization evolutions with reduced degrees of freedom. The proposed approach improves the computational efficiency while enabling similar or better SNR efficiency of the imaging experiments. We demonstrate its efficacy using numerical experiments.Theory
The CRB provides a lower bound on the variance of any unbiased estimator, which can be used to characterize the SNR efficiency of an MRF experiment. Given a set of representative MR tissue parameters {ϴ(l)}, we denote the CRB for the associated MRF experiment as C(ϴ). The early work minimizes the CRB while incorporating a constraint on the variation of flip angle2, which leads to improved reconstruction performance for highly-undersampled imaging experiments. This formulation imposes a flip angle constraint in a non-parametric manner. Despite its effectiveness in improving estimation performance, it often results in an expensive computational problem due to the large dimensionality of the search space and the convergence of the nonconvex and nonlinear optimization.Here we present a new experiment design approach with improved computational efficiency. Specifically, we introduce a B-spline based representation to parameterize the sequence of data acquisition parameters. B-splines are polynomial functions with compact support7. By properly choosing the order and number of the B-spline basis functions, we can constrain the acquisition parameters in some desirable low dimensional subspace. This constraint essentially serves as an effective regularizer for the optimal experiment design problem. Further, by using a low-dimensional spline space, we significantly reduce the number of degrees of freedom in comparison to the earlier method2. Mathematically, the proposed formulation can be described as follows:
$$ \begin{gather*} \min_{x_\alpha, x_{TR} } \sum_{l=1}^L \sum_{i=1}^3 \omega_i \sqrt{C(\theta^{\left(l\right)})_{ii}}/\theta_{ii}^{(l)}, \\ \text{s.t. } \, \alpha_n^{\text{min}} \leq (A_\alpha x_\alpha)_n \leq \alpha_n^{\text{max}}, \\ \hspace{.7cm} TR_n^{\text{min}} \leq (A_{TR} x_{TR})_n \leq TR_n^{\text{max}},\end{gather*}$$ where xα and xTR are the coefficients of the B-spline functions, and Aαxα and ATRxTR are the flip angle and repetition time schedules, respectively. Here the matrices Aα and ATR are determined by the B-spline basis functions used. We solve the resulting non-convex optimization problem using sequential quadratic programming8.
Methods and Results
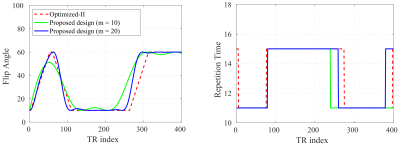
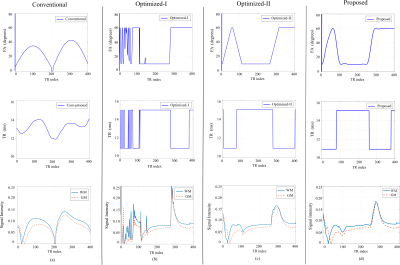
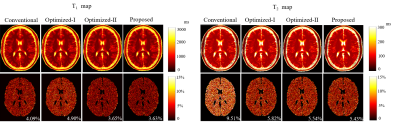
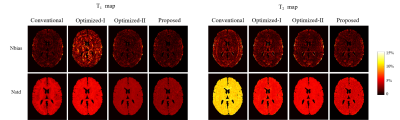
We evaluated the effectiveness of the proposed approach using numerical experiments and compare it with the conventional MRF experiment1 and the Optimized-I and Optimized-II approaches2. Figure 1 shows the optimized flip angle and repetition time schedule using the proposed approach with the number of B-spline basis = 10 and 20. Figure 2 includes the algorithm runtime for designing imaging experiments with acquisition lengths N = 300 and 400 using the different approaches. As can be seen, by constraining the acquisition parameters in a lower-dimensional spline space, the proposed approach provides a two order of magnitude improvement in computational efficiency. Figure 3 shows the acquisition parameters and the resulting magnetization evolutions from different MRF acquisition schemes. It is clear that the proposed approach with a parametric spline constraint enables a smooth magnetization evolution that is similar to Optimized-II but with significantly improved computational efficiency.We further evaluated the reconstruction/estimation performance using data acquisition parameters from conventional MRF experiments1, Optimized-I and II2, and the proposed approach (with the number of B-spline basis = 20). We simulated IR-FISP9 imaging experiments with a numerical brain phantom created using the Brainweb10 database and applied maximum likelihood reconstruction6 to reconstruct the MR tissue parameters. Figure 4 shows the reconstructed T1 and T2 maps and associated relative error maps at the acquisition length N = 400. Compared to the conventional MRF experiment design, the proposed spline-based design improves the accuracy of T2 by about a factor of 2, while slightly improving T1 accuracy. Further, it provides a slightly better reconstruction performance than the state-of-the-art approach, i.e., Optimized-II, but with a two-order magnitude improvement in the computational speed (as shown in Figure 2). Figure 5 shows the normalized bias and variance maps of T1 and T2 from Monte Carlo simulations with 100 trials. As can be seen, the proposed approach improves the estimation variance over Optimized-II. Also note that by incorporating either the non-parametric constraint (i.e., Optimized-II) or parametric constraint (i.e., proposed approach) on the flip angle schedule, we improve the estimation performance for T1, which is highly desirable.
Conclusion
In this work, we introduced a new approach for the optimal design of MRF data acquisition parameters with a B-spline based low-dimensional representation. Comparing to the state-of-the-art methods, the proposed approach improves the computational efficiency by two orders of magnitude, while achieving a similar or better SNR efficiency of the imaging experiments.Acknowledgements
This work was partially supported by the research grants NIH-R00EB027181 and NIH-R01EB017219.References
[1] D. Ma, V. Gulani, N. Seiberlich, K. Liu, J.L. Sunshine, J.L. Duerk, and M.A. Griswold. Magnetic resonance fingerprinting. Nature. 2013; 495(7440):187-192.
[2] B. Zhao, J.P. Haldar, C. Liao, D. Ma, Y. Jiang, M.A. Griswold, K. Setsompop, and L.L. Wald. Optimal Experiment Design for Magnetic Resonance Fingerprinting: Cramer-Rao Bound Meets Spin Dynamics. IEEE Trans Med Imaging. 2019; 38(3):844-861.
[3] P.K. Lee, L.E. Watkins, T.I. Anderson, G. Buonincontri, and B.A. Hargreaves. Flexible and efficient optimization of quantitative sequences using automatic differentiation of Bloch simulations. Magn Reson Med. 2019; 82(4):1438-1451.
[4] A. Lahiri, J.A. Fessler, and L. Hernandez‐Garcia. Optimizing MRF-ASL scan design for precise quantification of brain hemodynamics using neural network regression. Magn Reson Med. 2020; 83(6):1979-1991.
[5] J. Assländer, R. Lattanzi, D.K. Sodickson, M.A. Cloos. Optimized quantification of spin relaxation times in the hybrid state. Magn Reson Med. 2019; 82 (4), 1385-1397.
[6] B. Zhao, K. Setsompop, H. Ye, S.F. Cauley, and L.L. Wald. Maximum Likelihood Reconstruction for Magnetic Resonance Fingerprinting. IEEE Trans Med Imaging. 2016; 35(8):1812-1823.
[7] K. Höllig and J. Hörner. Approximation and Modeling with B-Splines. Society for Industrial and Applied Mathematics. 2013.
[8] J. Nocedal and S. J. Wright. Numerical Optimization. New York, NY, USA: Springer, 2006.
[9] Y. Jiang, D. Ma, N. Seiberlich, V. Gulani, and M.A. Griswold. MR Fingerprinting Using Fast Imaging with Steady State Precession (FISP) with Spiral Readout. Magn Reson Med. 2015; 74(6):1621-1631.
[10] D.L. Collins, A.P. Zijdenbos, V. Kollokian V, J.G. Sled, N.J. Kabani, C.J. Holmes, and A.C. Evans. Design and construction of a realistic digital brain phantom. IEEE Trans Med Imaging. 1998; 17(3):463-468.
Figures