Introduction

Magnetic Resonance Fingerprinting (MRF) has been used to simultaneously estimate T1 and T2 values using a balanced Steady-State Free Precession (bSSFP) acquisition¹. bSSFP-MRF retains the spin history and achieves high SNR and scan efficiency². However, banding artifacts produced by off-resonance effects in the bSSFP affect the quality of the tissue maps. In addition, spiral acquisition causes blurring due to off-resonance³. Here, we propose to apply a Generative Adversarial Network (GAN) mixed with the transformer blocks to correct for off-resonance effects in bSSFP-MRF sequence. The feasibility of the proposed approach was evaluated in simulations.

Method

Dataset: we generated simulations with realistic brain parameters coming from BrainWeb's dataset. We employed Flip Angles (FA) between 0º-80º after an RF inversion pulse, 1000 random Time Repetitions (TR) between 14.5-18.0 ms¹, balanced gradients in each TR, and a spiral readout of 18 interleaved. The FOV was 128 mm with a resolution of 2 mm.
Model Architecture: for the generator, we used a combination of two models. First, the encoder consists of a series of 1D convolutions and max pooling, and the bottleneck consists of several residual blocks similar to Earthquake Transformer⁴. We used transformer non-local attention blocks. For the decoder, we employed a single unit of the Earthquake Transformer's decoder. For the discriminator we used a projection discriminator⁵. As the objective function, we used a relativistic GAN loss⁶ :

$$\begin{align*}\mathcal{L}_{D} & =\mathbb{E}_{x_{r},x}\left[\left(C\left(x_{r},x\right)-\mathbb{E}_{x_{f},x}\left[C\left(x_{f},x\right)\right]-1\right){{}^2}\right]+\\ & \quad\,\mathbb{E}_{x_{f},x}\left[\left(C\left(x_{f},x\right)-\mathbb{E}_{x_{r},x}\left[C\left(x_{r},x\right)\right]+1\right){{}^2}\right]\\\mathcal{L}_{G} & =\mathbb{E}_{x_{r},x}\left[\left(C\left(x_{r},x\right)-\mathbb{E}_{x_{f},x}\left[C\left(x_{f},x\right)\right]+1\right){{}^2}\right]+\\ & \quad\,\mathbb{E}_{x_{f},x}\left[\left(C\left(x_{f},x\right)-\mathbb{E}_{x_{r},x}\left[C\left(x_{r},x\right)\right]-1\right){{}^2}\right]+\\ & \quad\,\mathbb{E}_{x_{f},x_{r}}\Vert x_{f}-x_{r}\Vert_{1}.\end{align*}$$

where $$$x_{r}$$$ is a sample from the conditional distribution of the on-resonance signal given the off-resonance signal, $$$x_{f}$$$ is a sample from the learned conditional distribution of the on-resonance signal given the off-resonance signal, and $$$x$$$ is a sample of the off-resonance signal distribution. Finally, we solved iteratively the following problems:

$$\begin{align*}\min_{G} & \mathcal{L}_{G}\\\min_{C} & \mathcal{L}_{D}.\end{align*}$$

Dictionary Generation: a Bloch simulator was used to generate fingerprints following a range of T1, T2 and df (off-resonance) values: T1(400 to 2000 ms, every 10 ms), T2 (40 to 300 ms, every 4 ms), and df (off-resonance, -250 to 250 Hz, every 2 Hz). The echo time (TE) was constant and equal to 7.25 ms for each TR. Tissue property maps were obtained by performing the measured signal to the closest dictionary entry using the maximum dot product.

Finally, to analyze the results we used the Normalized Mean Square Error $$$\mathrm{NMSE}\left(y,\hat{y}\right)=\frac{\Vert y-\hat{y}\Vert_{2}^{2}}{\Vert y\Vert_{2}^{2}}$$$, where $$$y$$$ represents the ground truth of the property maps (T1 or T2) and $$$\hat{y}$$$ is the estimation.

Results

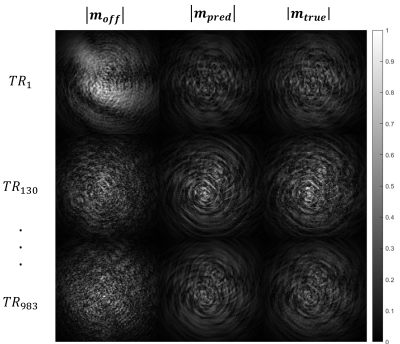
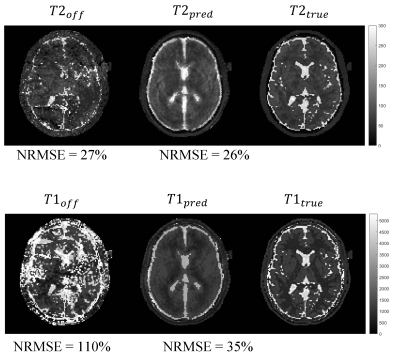
Figures 1 and 2 show a considerable qualitative improvement in the absolute and phase images for the different TRs. In the figure 3, we can see the off-resonance map. Note that this numerical phantom is heavily afected by off-resonance artifacts, with values raging from -100 Hz to 220 Hz. Figure 4 shows a comparison of the MRF reconstructed maps using the TR images with and without the off-resonance correction. The T1 NMSE was reduced from 110% (classical MRF) to 35% (off-resonance corrected). For T2 the NMSE was decreased from 27% to 26%.

Conclusion

A general approach based on GAN mixed with transformer blocks was proposed to correct for off-resonance distortions in bSSFP-MRF with spiral sampling. Our approach for off-resonance correction showed improved reconstructions in comparison to conventional bSSFP-MRF. Future work will validate the proposed approach in phantom and in-vivo acquisitions.