Synopsis

In this work, we investigate the influence of eddy currents on hybrid state free precession (HSFP) sequences with 3D radial (koosh-ball) readout trajectories and propose a simulated annealing-based algorithm to minimize their impact.

The proposed approach of reordering the temporal succession of radial spokes successfully minimized the influence of eddy currents on HSFP experiments. Although these results were shown in the context of a HSFP experiment, we believe that this approach could find a broader application in multi-shot bSSFP sequences.

Introduction:

The transient signal of fully balanced steady-state free precession (bSSFP) sequences has been used in various techniques to rapidly quantify relaxation times [1,2,3]. These techniques opt for a balanced sequence design due to the inherently high signal and strong dependence of both T₁ and T₂ on the signal behavior. At the same time, balanced sequences are more susceptible to eddy currents effects [4,5]. In this work, we investigate the influence of eddy currents on hybrid state free precession (HSFP) sequences with 3D radial (koosh-ball) readout trajectories and propose a simulated annealing-based algorithm to minimize their impact.

Theory:

During an HSFP experiment, the magnetization is driven adiabatically by smoothly varying flip angles (FA). For both, steady-state bSSFP and HSFP sequences, additional phases, caused by eddy currents, can lead the magnetization to oscillate orthogonally to the steady-state cone [4]. The occurrence of this effect becomes apparent when looking at the HSFP-condition [1]:
$$\mathrm{max}\{|\Delta\alpha|,|\Delta\phi|\}\ll\mathrm{sin}^2\frac{\alpha}{2}+\mathrm{sin}^2\frac{\phi}{2}$$
Here, $$$\alpha$$$ is the flip angle and $$$\phi$$$ the phase accumulated during a single TR ($$$\phi=\pi$$$ is called the on-resonance condition). When these conditions are fulfilled, no oscillating states are excited [1]. However, rapid changes in the k-space trajectory in consecutive TRs can cause a rapidly changing f via eddy currents, leading to image artifacts [4]. Therefore, we aim here at minimizing jumps in the k-space trajectory.

Methods:

For 3D HSFP experiments, the magnetization is driven into a periodic, dynamic equilibrium of predefined duration [1]. In the presented experiments, performed on a 3T PRISMA (Siemens Healthineers) with a 20-channel head coil, 189 or 190 repetitions of the FA-train were measured. Each cycle is 4 seconds long, resulting in a scan time of approximately 12.5mins for a head-equivalent FOV with 1.2mm isotropic resolution. During each cycle, i.e., cycles of the FA-train different radial spokes are acquired. Afterwards, a low rank alternating direction method of multipliers (ADMM) approach with a locally low rank penalty [6,7], implemented in BART [8], is used to reconstruct coefficient images in a compressed basis.
As a starting point, we adopted a multi-dimensional golden mean approach [9] and reordered the spokes such that the golden mean index first cycles through the repetitions of the same timeframe or flip angle index before jumping into the next timeframe:
$$\varphi_{i,j} = (nCyc\cdot i+j)\cdot\,2\pi\cdot\,GA_2$$
$$\theta_{i,j} = \mathrm{cos}^{-1} (\mathrm{mod}((nCyc\cdot i+j)\cdot\,GA_1,1))$$
Here, i is enumerating over the length of the FA-train, j is enumerating over the cycles, nCyc is the total number of cycles and GA₁ and GA₂ are 2D-golden mean ratios with respective approximate values of 0.4656 and 0.6823 [9].
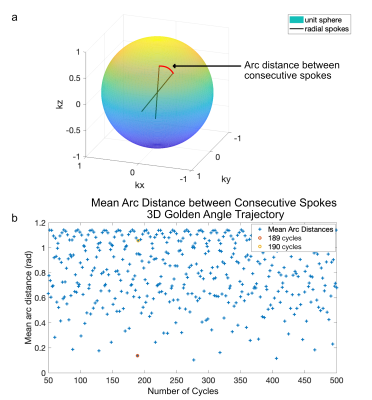
This readout trajectory design ensures adequate sampling of k-space within each timeframe, can however lead to large angular jumps between consecutive readout directions, as illustrated in Fig.1b. We thus propose a simulated annealing based algorithm¹ which aims to reorder any predefined set of readout directions {$$$\varphi_{i,j},\theta_{i,j}$$$}, therein minimizing the Euclidean distance between consecutive readouts.
In a phantom study, 3 different trajectories were compared: Firstly, the GA trajectory defined by Eq.(2-3) with 189 cycles, which should result in little influence of eddy currents according to Fig.1b. Secondly, a GA trajectory with 190 cycles, where the average distance between consecutive readout directions is large. Lastly, a set of randomly drawn readout directions. These sets of readout directions were subsequently reordered to minimize the impact of eddy currents.

Results:

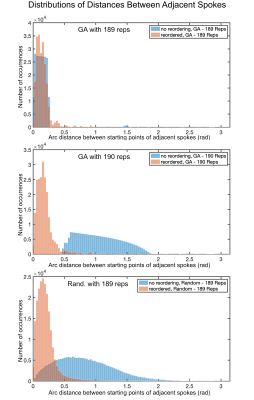
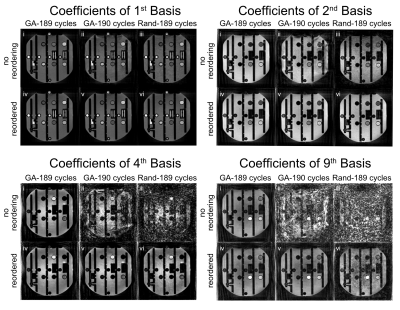
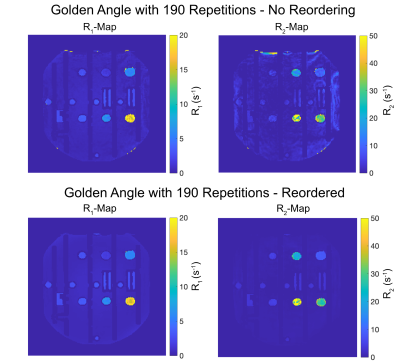
Fig.2 shows the arc distance distribution for each of the investigated patterns before and after reordering. The GA trajectory with 189 cycles already shows mostly small changes in the orientation of readouts, as was expected from Fig.1. The GA trajectory with 190 cycles and the random trajectory have a substantially worse distribution and thus the reordering significantly reduces the average angular change between spokes from 1.05rad to 0.2rad and from 0.82rad to 0.21rad, respectively.
Fig.3 shows the reconstructed coefficient images for each sequence. For the scans without reordering, only the scan with 189 cycles shows acceptable image quality for the 4^th basis and beyond. After reordering, all trajectories show good image quality, which in turn improves the quantitative maps derived from these coefficient images, see Fig.4.

Discussion:

The proposed approach of reordering the temporal succession of radial spokes successfully minimized the influence of eddy currents on HSFP experiments. This tool allows an arbitrary number of cycles to be used for the GA trajectory and enables the use of different kinds of spoke distributions, such as random patterns. The coefficient image of the random distribution, however, displays a lower SNR in the 9th basis. This might be linked to a suboptimal coverage of k-space.
Although these results were shown in the context of an HSFP experiment, we believe that this approach could find a broader application in multi-shot bSSFP sequences.

Acknowledgements

No acknowledgement found.