1550
MR Fingerprinting Reconstruction based on Structured Low-rank Approximation and Subspace Modeling
Peng Li1 and Yue Hu1
1Harbin Institute of Technology, Harbin, China
1Harbin Institute of Technology, Harbin, China
Synopsis
Due to the capability of fast multi-parametric quantitative imaging, magnetic resonance fingerprinting has become a promising quantitative magnetic resonance imaging (QMRI) approach. However, the highly undersampled and noise-contaminated k-space data will cause critical spatial artifacts, which subsequently lead to inaccurate estimation of the quantitative parameters. In this paper, we introduce a novel framework based on structured low-rank approximation and subspace modeling to recover temporal MRF data from its highly undersampled and noisy Fourier coefficients.
Introduction
Magnetic resonance fingerprinting (MRF)1 is a recently proposed quantitative imaging technique, which uses combinations of random RF pulse sequences to simultaneously obtain multiple tissue parameters, such as $$$\rm T_1$$$ and $$$\rm T_2$$$ relaxation times, and proton density (PD). Generally, in order to accelerate the data acquisition, high undersampling rate is applied, leading to severe spatial artifacts, which correspondingly have negative impact on the accurate estimation of the quantitative parameters of tissues. A number of MRF reconstruction methods have recently been proposed to overcome undersampling artifacts, resulting in improvements in accuracy and computational efficiency. Some scholars proposed methods based on compressed sensing2 and singular value decomposition3 to improve the performance of MRF to varying degrees. However, they do not take advantage of the temporal similarity of the collected data. Mazor et al.4 and Zhao et al.5 introduced the low-rank and subspace modeling to reconstruct artifact-free time frames, which can explore the temporal correlation of the MRF data. Fourier-domain structured low-rank matrix priors have been introduced into MRI reconstruction6 and provide improved reconstruction over classical low‐rank regularization and total variation methods. In this paper, we propose a novel framework based on structured low-rank approximation and subspace modeling in order to improve the MRF reconstruction results..Methods
In MRF, data acquisition is performed in the $$$k$$$-space , which can be modeled as:$$$\mathbf b={\cal A}(\mathbf x) + \mathbf n$$$
where $$$\mathbf x \in \mathbb{C}^{N \times N \times L} $$$ represents the distortion-free Fourier coefficients to be recovered, $$${\cal A}: \mathbb{C}^{N \times N \times L} \rightarrow \mathbb{C}^{Q \times L}$$$ is a linear degradation operator which maps $$$\mathbf{x}$$$ to $$$\mathbf{b}$$$, $$$Q$$$ is the number of $$$k$$$-space samples in each frame, and $$$\mathbf{n} \in \mathbb{C}^{Q \times L}$$$ is the Gaussian distributed white noise. $$$\mathbf{b}$$$ is the acquired highly undersampled, noisy Fourier coefficients. Based on the assumption that the time sequences of MRF data can be modeled as three-dimensional (3D) piecewise constant functions, we consider the recovery problem of MRF by using structured matrix liftings6 $$${\cal T}(\mathbf x)$$$ (Fig.1) and the Schatten-$$$p$$$ ($$$0\leq p<1$$$) quasi-norms6, which can be formulated as the following optimization problem:
$$$\min_{\mathbf{x}} \left\lVert {\cal A}(\mathbf{x})-\mathbf{b}\right\rVert_2^2+\lambda \left\lVert {\cal T}(\mathbf{x}) \right\rVert_p^p$$$
where $$$\lambda>0$$$ is a tunable regularization parameter. This problem can be efficiently solved using the GIRAF algorithm7. During each iteration, the subspace modeling is applied to project the time domain data into the dictionary space to further improve the accuracy of the reconstruction, which can be formulated as:
$$$\cal{P}(\cal{X})=\cal{X}\mathbf{D}^\dagger \mathbf{D}$$$
where $$$\mathbf{D}$$$ is an orthonormal basis for dictionary $$$\mathbb{D}$$$, and $$$\mathbf{D}^\dagger$$$ represents the Moore-Penrose pseudo-inverse of $$$\mathbf{D}$$$.
Results and discussion
In the experiment, $$$\rm T_1$$$, $$$\rm T_2$$$ and PD parameter matrices, each with size of $$$128\times 128$$$, which were obtained by DESPOT1 and DESPOT2, were used as the ground truth. Variable density spiral trajectories with inner region size of 20 and FOV of 24 were used to acquire 876 $$$k$$$-space coefficients in each frame, with the acceleration factor of $$$\sim$$$20. In addition, in order to simulate the noisy undersampled MRF data, we added complex Gaussian white noise with $$$\sigma =0.5$$$ to the $$$k$$$-space data. We study the improvement of the image quality offered by the proposed method over the conventional MRF algorithm (MRF)1, and the MRF method with low-rank constraint (FLOR)4.In Fig.2, we plot the reconstruction results using the noiseless undersampled data with the acquisition length of 400. The first column shows the ground truth maps. The second, third, and fourth rows indicate the reconstructed maps of T1, T2, and PD using MRF, FLOR, and the proposed method, respectively. Fig.3 shows the error maps with respect to the ground truth. We observe that the proposed method provides the reconstructed maps with the highest accuracy. Fig.4 show the reconstructed maps using different methods with the noise-contaminated $$$k$$$-space data with the acquisition length of 400. Fig.5 indicate the error images. It is shown that our method performs the best, which is consistent with the noiseless scenario.
Conclusion
We present a novel framework for high-quality reconstruction of MRF data. By remodeling the MRF data as structured low-rank Toeplitz matrix and applying the subspace modeling, we are able to accurately reconstruct the MRF data from its highly undersampled, noisy Fourier coefficients, and thus further improve the accuracy of multiparametric quantitative imaging. The experiments have demonstrated the improved performance of the proposed method compared with the state-of-the-art algorithms.Acknowledgements
No acknowledgement found.References
- Dan Ma, Vikas Gulani, Nicole Seiberlich, Kecheng Liu, Jeffrey L Sunshine, Jeffrey L Duerk, and Mark A Griswold, “Magnetic resonance fingerprinting,” Nature, vol. 495, no. 7440, pp. 187–192, 2013.
- Mike Davies, Gilles Puy, Pierre Vandergheynst, and Yves Wiaux, “A compressed sensing framework for magnetic resonance fingerprinting,” SIAM Journal on Imaging Sciences, vol. 7, no. 4, pp. 2623–2656, 2014.
- Debra F McGivney, Eric Pierre, Dan Ma, Yun Jiang, Haris Saybasili, Vikas Gulani, and Mark A Griswold, “Svd compression for magnetic resonance fingerprinting in the time domain,” IEEE transactions on medical imaging, vol. 33, no. 12, pp. 2311–2322, 2014.
- Gal Mazor, Lior Weizman, Assaf Tal, and Yonina C Eldar, “Low-rank magnetic resonance fingerprinting,” Medical physics, vol. 45, no. 9, pp. 4066–4084, 2018.
- Bo Zhao, Kawin Setsompop, Elfar Adalsteinsson, Borjan Gagoski, Huihui Ye, Dan Ma, Yun Jiang, P Ellen Grant, Mark A Griswold, and Lawrence L Wald, “Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling,” Magnetic resonance in medicine, vol. 79, no. 2, pp. 933–942, 2018.
- Yue Hu, Xiaohan Liu, and Mathews Jacob, “A generalized structured low-rank matrix completion algorithm for mr image recovery,” IEEE transactions on medical imaging, vol. 38, no. 8, pp. 1841–1851, 2018.
- Gregory Ongie and Mathews Jacob, “A fast algorithm for convolutional structured low-rank matrix recovery,” IEEE transactions on computational imaging, vol. 3, no. 4, pp. 535–550, 2017.
Figures
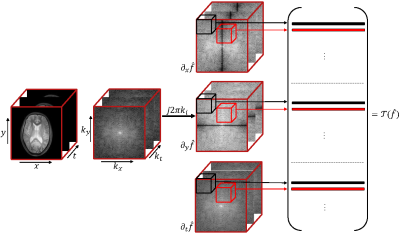
Fig.1 Illustration of the structure of the lifted matrix $$${\cal T}(\mathbf{x})$$$: The rows of the matrix are 3-D neighborhoods of the gradient-weighted $$$k$$$-space samples.
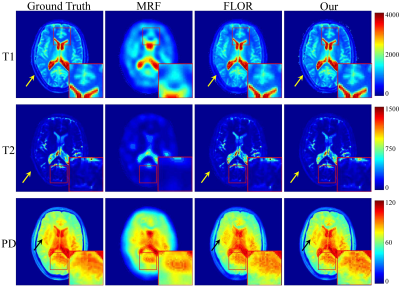
Fig.2 Reconstructed maps of T1, T2 and PD, using the 5% sampled noiseless data. The acquisition length is $$$L=400$$$.
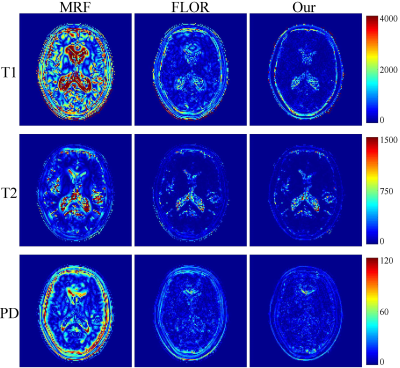
Fig.3 Error maps of T1, T2, and PD using 5% of noiseless $$$k$$$-space samples, with acquisition length $$$L=400$$$.
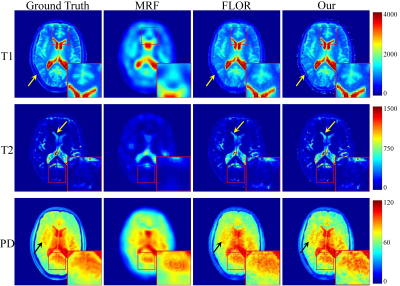
Fig.4 Reconstructed maps of T1, T2 and PD, using the 5% sampled noisy data. The acquisition length is $$$L=400$$$.
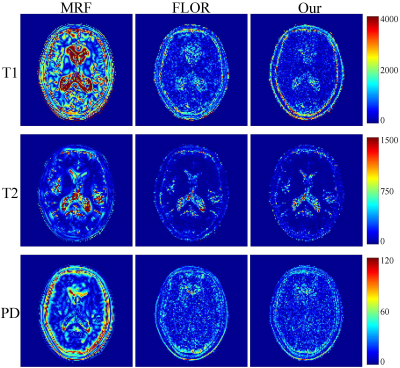
Fig.5 Error maps of T1, T2, and PD using 5% of noisy $$$k$$$-space samples, with acquisition length $$$L=400$$$.