Introduction

Magnetic resonance fingerprinting (MRF) is a novel quantitative MRI (qMRI) technique [1]. 3D MRF has been developed for further acceleration of parametric quantitation [2], [3]. Due to the relatively high undersampling factor in k-space and the flexible k-t sampling pattern, several iterative reconstruction methods have been proposed. While in the 3D MRF case, a dynamic 3D MRF data matrix would be memory consuming, thus limited the use of iterative reconstruction. In this work, a k-space compression strategy is proposed in a 3D alternating direction method of multipliers (ADMM) [4] framework, where both k-space data and image series are compressed, and computation is efficiently improved.

Methods

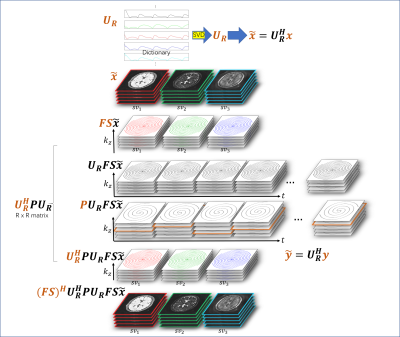
3D ADMM MRF framework
The optimization problem of MRF can be written as $${x,z}=\mathop{\text{argmin}}_{x,z} \left\| {F}{S}{x}-{y}\right\|_2 \quad\text{s.t.} \quad {x} - {z} = 0 (1) $$ Where y is the raw data, x is the image series, FS is the encoding matrix with coil sensitivity, and z is the projection of x to the dictionary $$$\Pi_{T_1,T_2,\rho} (x) \quad\quad$$$.
Data compression for MRF
For MRF, raw data in k-space and image series have extremely large dimensions, including k-space data points $$$N_k$$$, number of phase encodings $$$N_p$$$, and number of time points $$$N_t$$$, which consume memory during computation. Thus, the reconstruction of large-scale data matrices is expensive. Specifically, the calculation of $$$A^{H} Ax = (FS)^{H}PFSx$$$ (where $$$S$$$ sensitivity map, $$$F$$$ Fourier transform, $$$P$$$ k-space undersampling mask, and $$$ A=PFS $$$ encoding matrix) can be challenging, considering the image series $$$x$$$ usually takes up > 10 GB memory for a dynamic 3D data matrix. Here, we utilize a singular value decomposition (SVD) based k-space compression method, leading to a significant reduction in computer memory usage and computation time. For MRF, the raw data (and signal evolution) can be well approximated by using a dictionary matching method, as was used in the MRF approach. Dictionary entries $$$D$$$ raw k-space data $$$y$$$ and image series $$$x$$$ can be compressed with SVD (as shown in Fig. 1), i.e.,$$$\widetilde{D}=U_R^H D$$$, $$$\widetilde{y}=U_R^H y$$$, and $$$\widetilde{x}=U_R^H x $$$, where $$$\Delta=U_R^H \Sigma U_R$$$, $$$R$$$ is the number of coefficients in subspace projection, and $$$U_R$$$ is the concatenation of $$$N_p$$$ repeated $$$U_R$$$. For example, the calculation for forward and backward operations for $$$A$$$ on $$$x$$$ is $$A^{H} Ax = (FS)^{H}PFSx \quad\quad(2)$$ The modified calculation with $$$\widetilde{A} = PFSU_R$$$, i.e., for compressed k-space, is $$\widetilde{A}^H \widetilde{A}\widetilde{x}= U_R^H(FS)^HPFSU_R\widetilde{x}\quad\quad(3)$$ Where $$$P$$$ is determined by the undersampling pattern of the k-space trajectories. Note that $$$U_R$$$ and $$$FS$$$ commute because $$$FS$$$ operates spatially while $$$U_R$$$ works temporally. Using the commutative property, Eq. 3 is converted to $$\widetilde{A}^H \widetilde{A}\widetilde{x}= (FS)^HU_R^HPU_RFS\widetilde{x}\quad\quad(4)$$ Therefore, the only difference between Eq. 2 and Eq. 4 is that $$$P$$$ is replaced by $$$U_R^H P U_R $$$ for a compressed k-space. More importantly, the size or the computation cost of encoding matrix $$$FS$$$, can be reduced because $$$\widetilde{x}$$$ is compressed as well. In addition, $$$U_R^H P_{p,q} U_R $$$ has a matrix size of , which is a very small matrix size for each trajectory (p,q) in k-space. With precalculated $$$U_R^H P_{p,q} U_R $$$, intermediate calculation of $$$\widetilde{A}^H \widetilde{A} $$$ can be significantly simplified. In addition, given the number of phase encoding/readout trajectories $$$N_{traj}$$$ and according to the undersampling pattern along different time points, the temporal dimension of raw data $$$\widetilde{y}$$$ is compressed from size of $$$N_t$$$ to $$$R\times N_{traj}$$$ by pre-calculating $$$U_R^H y$$$ before the reconstruction iteration. Based on the MRF scheme, can be as small as four in our previous study, i.e., data can be compressed to four ‘complete’ k-space, $$$\widetilde{y}$$$, leading to efficient computation.
Acquisition
3D MRF data were acquired with stack-of-spiral readout with shuffled sampling pattern. 1000 time frames were acquired in each repetition, and different kz positions were sampled in different repetitions. 5s delay time, as well as an IR pulse, was added between consecutive repetitions. FOV for the whole brain was 256x256x144 mm, and the resolution was 1x1x3 mm. The scan time for an undersampling R= 3 (along kz) was 4 min and 30s. All data were acquired in a GE Signa 3.0T (General Electric Healthcare) scanner with a 48 channel head coil.

Results

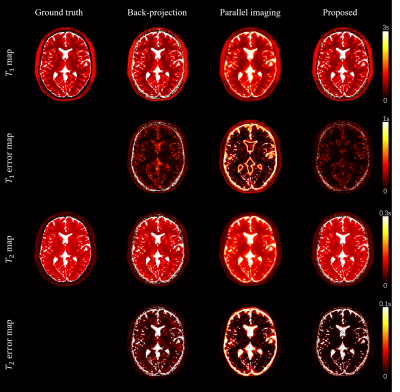
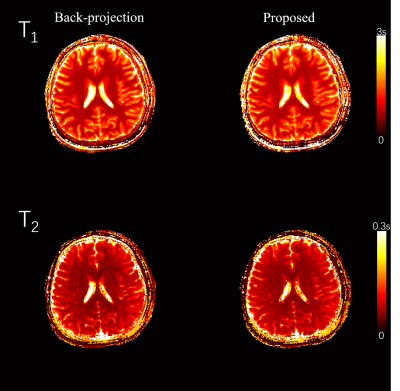
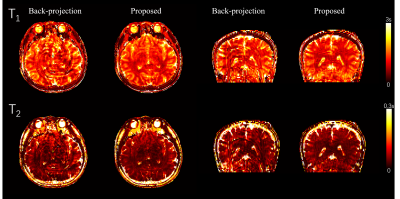
Fig 2 and Fig 3 show the 2D and 3D simulation results. The reconstruction performance of back projection, parallel imaging, and the proposed method are compared with the gold standard numerical phantom. Fig 4 shows the 2D in vivo result with 300x300 FOV and 400-time frames. Underestimation on the T2 map from backprojection method was slightly improved in the proposed method. Fig 5 shows the 3D in vivo result, acquired using a stack of spiral MRF. Severe artifacts resisted in the backprojection method, while they were effectively reduced with the proposed method.

Discussion

Whole-brain 3D MRF data can be acquired in 4 min and 30s with the proposed method, and acceptable quantitative maps are generated by this reconstruction algorithm. By simulation and in-vivo scans, our proposed method significantly improves the reconstruction performance compared to the conventional backprojection method. With the compression on k-space, the computation cost is reduced, and the 3D ADMM can thus be performed with finite memory.

Acknowledgements

No acknowledgement found.