1542
Multi-compartment MR Fingerprinting: an off-the-grid approach1University of Bath, Bath, United Kingdom
Synopsis
We introduce a novel off-the-grid sparse approximation algorithm to separate multiple tissue compartments in image voxels and to estimate quantitatively their NMR properties and mixture fractions, given the MR fingerprinting (MRF) measurements. The proposed algorithm is an accurate and importantly a scalable alternative to the multicompartment MRF baselines because it does not rely on fine-gridded multiparametric MRF dictionaries. The method is theoretically described, and its feasibility is demonstrated and compared to other baselines on in-vivo healthy brain measurements.
Purpose:
Multi-Compartment (MC) or partial volume effects occur when more than one tissue type occupies a single image voxel. The Magnetic Resonance Fingerprinting (MRF)1 is not exempted from MC effects: if left unmodelled they can produce false and blurry quantitative mappings at the tissue boundaries. Hence estimating these effects is crucial for obtaining accurate segmentation and estimation of the tissue volumes and their contents. Current algorithms2,3,4 for solving MC-MRF rely on sparse approximation in a discretised dictionary of Bloch responses. However, fine-grid discretisation of the NMR properties creates large and highly coherent MRF dictionaries that can challenge scalability and precision of the numerical methods for (discrete) sparse approximation. To overcome these issues, we propose an off-the-grid approach equipped with simultaneous compartment-wise and voxel-wise sparsity regularisations using continuous (non-discretised) Bloch response models.The problem and the algorithm:
Given a Time-Series of Magnetisation Images (TSMI) $$$X\in R^{T\times v}$$$ with $$$v$$$ voxels and $$$T$$$ timeframes, in multicompartment MRF (MC-MRF) we are interested in the following decomposition: $$X=\sum_s \varphi(\theta_s)C_s^{T}$$for estimating sparse number of tissue compartments across the entire image characterised by their NMR properties $$$\theta_s$$$ e.g. $$$\theta_s=(T1_s,T2_s)$$$ in T1/T2 relaxometry, as well as their non-negative mixture maps $$$C_s \in R^v$$$ indicating each compartment’s weight/fraction in image voxels. A model for Bloch responses $$$\varphi(.): R^{|\theta|} \rightarrow R^T$$$ is given, but the number of compartments is unknown.
Following off-the-grid compressed sensing literature5, we can recast the above problem as of finding weighted Dirac’s mass functions composed by a continuous dictionary $$$\Phi$$$:
$$X=\Phi m := \int \varphi(\theta) dm(\theta), \,\,\,\,\, where\,\,\, m=\sum_s C_s^T \delta(\theta-\theta_s).$$
Dirac spikes $$$\delta(.)$$$ are weighted by the mixture fractions, and the task is to approximate the weights and spike positions similar to the conventional compressed sensing, but with a notable difference that the spike positions are not discretised (hence we avoid building large MRF dictionaries) and they can take value in the continuous space of $$$\theta=(T1,T2)$$$ (hence we can expect better precision).
To combat problem’s ill-posedness, we regularise solutions to have two types of structures simultaneously: to be composed of sparse compartments in the sum and additionally, each mixture map $$$C_s$$$ itself to be a sparse image. To do so, we propose solving the Sparse Group Buerling Lasso (SBG-Lasso) regularisation6,7:
$$ argmin_m \| X-\Phi m\|_F^2 + \alpha(1-\beta)\|m\|_1 + \alpha\beta\sqrt{v} \|m\|_2$$
where $$$\|m\|_1=\sum_s \|C_s\|_1$$$ and $$$\|m\|_2=\sum_s \|C_s\|_2$$$. The latter norm promotes group-sparsity i.e. few compartments approximate the entire TSMI across all voxels. The former norm promotes spatial (voxel-wise) sparsity within the mixture maps, for having some level (not necessarily 100%) of voxel purity that helps spatial separability of the mixture maps. Parameter $$$0<\beta<1$$$ balances between these priors, whereas $$$ \alpha>0$$$ controls the overall regularisation.
An iterative algorithm is proposed to solve this problem (for details see6). This algorithm requires iteratively differentiating and evaluating Bloch responses, which can be numerically challenging/slow in e.g. the EPG-type Bloch simulators8 adopted by MRF protocols such as FISP9. To address this, we use a pre-trained neural network6,10 to efficiently/fast approximate Bloch responses and differentiate them via back-propagation.
Experiments, results and discussion:
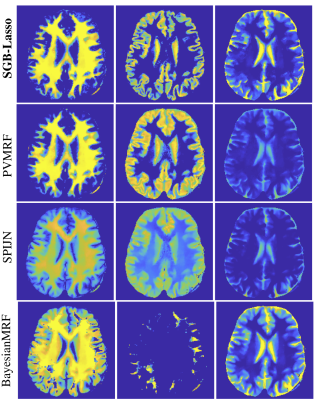
Experiments adopted a T1/T2-encoding sequence similar to FISP: same sinusoidal flip angles, fixed TR/TE = 10/1.9 ms, Tinv= 18 ms and 1000 repetitions. A 1.5T GE HDxT scanner with 8-channel RF coils acquired a healthy volunteer brain (in-vivo) measurements. Scanning parameters were 230x230mm2 FOV, 230x230 image size, 5mm slice thickness, variable-density spiral sampling, 377 interleaves, 920 kspace samples per TR.The dictionary-free LRTV MRF reconstruction10 was used to compute aliased-free and dimension reduced (T=10) TSMI from kspace data. TSMI were then phase-corrected4,6 before the MC-MRF step. We compared SGB-Lasso to the MC-MRF baselines SPIJN4, BayesianMRF2 and PVMRF3. Baselines required directly using a 8’540-atoms MRF dictionary for discretising the space $$$(T1,T2) \in [10,6000]\times[4,4000]$$$ ms. Our algorithm SGB-Lasso instead used a pre-trained small neural-network with one hidden layer of 500 neurons to embed the EPG responses in a differentiable function (see network/training details in6). Hyperparameters were grid-searched for all algorithms e.g. $$$\alpha=0.8, \beta=10^{-3}$$$were used for SGB-Lasso. Further, the outcomes of all algorithms were thresholded to visualise exactly three dominant compartments, expectedly related to the white matter (WM) and grey matter (GM) and the CSF.
Figure 1 shows the estimated mixture maps. Figure 2 compares the estimated T1/T2 values of WM and GM to their literature values at 1.5T. All methods’ CSF relaxations were underestimated (previously observed for FISP9) and not reported. We observe that SGB-Lasso outperforms the baselines in terms of the visual appearance and spatial separability of the mixture maps, and their correspondence to the anatomical structures of WM, GM and CSF. Further, the estimated relaxations for WM and GM are consistent with the literature. We observe that a voxel-sparsity alone (BayesianMRF) results in inferior demixing performance compared to the group-sparse models (PVMRF, SPIJN). The SGB-Lasso improves upon both approaches by simultaneously promoting both sparsity types and achieving a desired level of voxel purity within the sparse compartments’ mixture maps. Figure 3 further shows comparable runtimes for the SGB-lasso and the baselines.
Acknowledgements
No acknowledgement found.References
[1] D. Ma et al., “Magnetic resonance fingerprinting,” Nature, vol. 495, no. 7440, pp. 187–192, 2013.
[2] D. McGivney et al., “Bayesian estimation of multicomponent relaxation parameters in magnetic resonance fingerprinting,” Magnetic resonance in medicine, vol. 80, no. 1, pp. 159–170, 2018.
[3] A. Deshmane et al., “Partial volume mapping using magnetic resonance fingerprinting,” NMR in Biomedicine, vol. 32, no. 5, p. e4082, 2019.
[4] M. Nagtegaal, P. Koken, T. Amthor, and M. Doneva, “Fast multi- component analysis using a joint sparsity constraint for mr fingerprint- ing,” Magnetic resonance in medicine, vol. 83, no. 2, pp. 521–534, 2020.
[5] V. Duval and G. Peyre, “Exact support recovery for sparse spikes deconvolution,” Foundations of Computational Mathematics, vol. 15, no. 5, pp. 1315–1355, 2015.
[6] M. Golbabaee, and C. Poon. "An off-the-grid approach to multi-compartment magnetic resonance fingerprinting." arXiv preprint arXiv:2011.11193, 2020.
[7] C. Poon and M. Golbabaee, “The sparse-group beurling-lasso,” University of Bath, https://cmhsp2.github.io/files/journal/sparse group blasso. pdf, Tech. Rep., 2020.
[8] M. Weigel. "Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple," Journal of Magnetic Resonance Imaging, vol. 41, pp. 266-295, 2015.
[9] N. Jiang et al.,“MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout,” Magnetic resonance in medicine, vol. 74, no. 6, pp. 1621–1631, 2015.
[10] M. Golbabaee et al., “Compressive mri quantification using convex spatiotemporal priors and deep auto-encoders,” arXiv preprint arXiv:2001.08746, 2020.
[11]J G. Sled and G. B. Pike, “Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using mri,” Magnetic Resonance in Medicine, vol. 46, no. 5, pp. 923–931, 2001.
[12] G. J. Stanisz et al., “T1, t2 relaxation and magnetization transfer in tissue at 3t,” Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, vol. 54, no. 3, pp. 507–512, 2005.
Figures