1538

Human cerebral cortex parcellation using time-fractional order magnetic resonance fingerprinting (MRF)

Shahrzad Moinian^1,2, David Reutens^1,2, and Viktor Vegh^1,2
¹Centre for Advanced Imaging, The University of Queensland, Brisbane, Australia, ²ARC Training Centre for Innovation in Biomedical Imaging Technology, The University of Queensland, Brisbane, Australia

Synopsis

We have previously shown the potential efficacy of a magnetic resonance fingerprinting (MRF) residual approach for human cerebral cortex parcellation. However, the classical Bloch equations, commonly used for MR signal simulation in the MRF dictionary, may not accurately describe the complex effect of the ensemble of microarchitectonic components of the gray matter tissue on MRF signal. This work benefitted from the more flexibility of the extended time-fractional order Bloch equations to improve MRF dictionary fitting accuracy. We demonstrated that the time-fractional order parameter α potentially associates with the effect of interareal architectonic variability, hypothetically leading to more accurate cortical parcellation.

Introduction

Delineation of regions of the human cerebral cortex in individuals (i.e. cortical parcellation) is fundamental for understanding structure-function associations in the brain,¹ and may shed light on aging and disease effects on different cortical regions.^{2, 3} Accurate voxel-level parcellation could also improve delineation of abnormal tissue in the surgical setting (e.g. refractory epilepsy).^{4, 5} Current in vivo individual-specific parcellation methods mostly exploit MR relaxometry parameters.^6-9 However, recent research has shown their inability to distinguish interareal structural variations across the entire cortex.^10-13
MRF is a multi-parametric tissue property mapping framework that relies on unique tissue-specific signals generated by varying MR sequence acquisition parameters (e.g. flip angles, repetition times, echo times) pseudo-randomly.¹⁴ The fingerprinting component arises from a precomputed dictionary of simulated MR signals which are matched to each voxel’s acquired MR signal. Tissue parameters of the corresponding dictionary entry are then assigned to each voxel. The MRF process has relied on the Bloch equations and its parameters to produce individual signal evolutions for comparison with acquired MR data.
Previously, we introduced a novel approach for in vivo cortical parcellation based on MRF signals, after adjusting for the effects of MR relaxometry parameters (i.e. MRF residuals).¹⁵ We demonstrated the presence of additional area-specific information in the residuals, enabling parcellation of specific cortical areas in six participants.¹⁵ The complexity of the combined effects of microstructural constituents in human gray matter on MRF signal relaxation may not be described accurately and comprehensively by the classical Bloch equations. Here, we consider the utility of time-fractional order Bloch equations¹⁶ for human cortical parcellation. This extension to the classical Bloch equations provides additional flexibility in MRF signal fitting through the fractional-order exponents, parameters previously shown to be influenced by tissue microstructural constituents.¹⁶

Methods

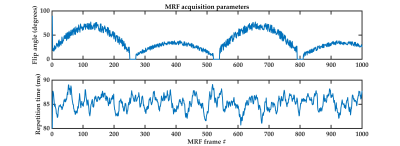
Six female participants aged 27-33 years underwent 1000-frame MRF scans (Figure1) on a 7T whole-body MR scanner (Siemens Healthcare, Erlangen, Germany), using a 2D EPI-MRF sequence as described previously.¹⁵
We used the following time-fractional order Bloch equations,¹⁶ refer to Eq.1, to simulate anomalous relaxation for MRF signal evolution generation comprising dictionary entries.

Eq.1)$$M_x^{'}\left(t\right)=\frac{M_{x}\left(0\right)-iM_{y}\left(0\right)}{2}E_{\alpha}\left(-\frac{\tau_2^{1-\alpha}t^{\alpha}}{T_2^*}+i{\Delta}{\omega}\tau_2^{1-\alpha}t^{\alpha}\right)+\frac{M_{x}\left(0\right)+iM_{y}\left(0\right)}{2}E_{\alpha}\left(-\frac{\tau_2^{1-\alpha}t^{\alpha}}{T_2^*}-i{\Delta}{\omega}\tau_2^{1-\alpha}t^{\alpha}\right)$$$$M_y^{'}\left(t\right)=\frac{M_{y}\left(0\right)+iM_{x}\left(0\right)}{2}E_{\alpha}\left(-\frac{\tau_2^{1-\alpha}t^{\alpha}}{T_2^*}+i{\Delta}{\omega}\tau_2^{1-\alpha}t^{\alpha}\right)+\frac{M_{y}\left(0\right)-iM_{x}\left(0\right)}{2}E_{\alpha}\left(-\frac{\tau_2^{1-\alpha}t^{\alpha}}{T_2^*}-i{\Delta}{\omega}\tau_2^{1-\alpha}t^{\alpha}\right)$$$$M_{z}\left(t\right)=M_{z}\left(0\right)E_{\alpha}\left(-\frac{\tau_1^{1-\alpha}t^{\alpha}}{T_{1}}\right)+\frac{M_{0}}{T_{1}}t^{\alpha}E_{\alpha,\alpha+1}\left(-\frac{\tau_1^{1-\alpha}t^{\alpha}}{T_{1}}\right)$$
Here, M_x and M_y denote transverse magnetization and M_z represents longitudinal magnetization. T1, T2^* and Δω indicate the spin-lattice relaxation time, spin-spin relaxation time and off-resonance precession frequency, respectively. t is the time elapsed since magnetization excitation by the radiofrequency pulse, α denotes the time-fractional order of anomalous relaxation, and τ₁ and τ₂ are unit preservation constants set to 1 in Eq.1. $$$E_{\alpha,\beta}\left(t\right)=\sum_{k=0}^\infty\frac{t^{k}}{\Gamma\left({\alpha}k+\beta\right)}$$$ is the two-parameter Mittag-Leffler function.¹⁷ Note, transverse and longitudinal magnetization processes were assumed to follow the same α-order process.
The MRF dictionary covers a combination of T1 values (500-1000ms, 1010-2010ms, 2010-3000ms, and 3030-3500ms in steps of 10ms, 20ms, 30ms, and 40ms, respectively), T2^* (10-60ms in steps of 2ms, and 60-100ms in steps of 3ms), off-resonance frequency ($$${\Delta}f=\frac{{\Delta}\omega}{2\pi}$$$) values (0-50Hz in 5Hz increments), transmit magnetic field (B1⁺) ratio (0.6-1.2 in 0.05 increments), and time-fractional order (α) values (0.6 -1 in 0.02 increments).
Across ten cortical regions-of-interest (ROI) (BA2, BA4, BA6, 7A, 7P, 7PC, 5L, 5M, 5Ci and hIP3) of six participants, we compared the accuracy of voxel-wise MRF dictionary fitting between three MRF dictionaries generated using Eq.1 when:

α≠1 and Δf≠0, i.e. Eq.1 is the extended model,¹⁶ which considers field inhomogeneity dephasing effects on the magnetization.
α≠1 and Δf=0, i.e. Eq.1 becomes the Magin’s fractional-order model,¹⁷ which assumes T2-weighted data and does not consider magnetization dephasing.
α=1 and Δf=0, i.e. Eq.1 becomes the classical integer-order Bloch equations resulting in signal evolution with mono-exponential decay.

The dot product between the voxel’s actual MRF signal and the best matching dictionary entry was used to evaluate how well the best matching signal simulation explains the measured MRF signal. Mean-squared-error (MSE) of MRF residual signal was also used as another dictionary fitting performance measure. The smaller the residual, the better the dictionary entry matches the measured signal.

Results and Discussion

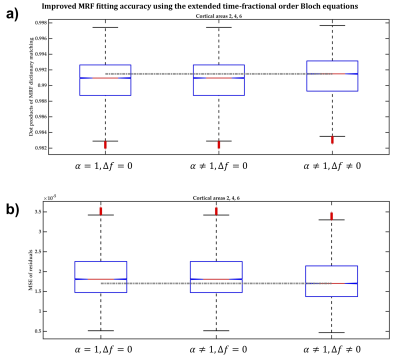
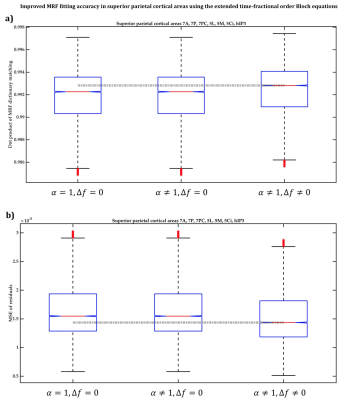
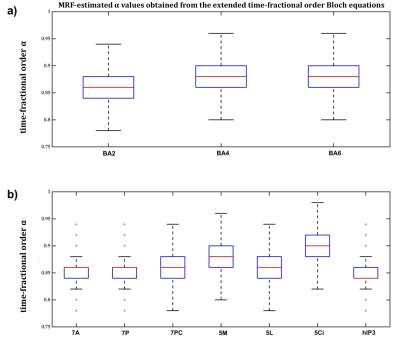
In BA2, BA4 and BA6, the dot products when the extended Bloch equations were used were significantly larger, with 95% confidence, than when Magin’s or the classical models were used (Figure2a) and the MSE of MRF residuals was significantly smaller (Figure2b), indicating a better match between the simulated and measured MRF signals. Fitting accuracy was slightly better with Magin’s model than with the classical model, but the difference was statistically insignificant. Similar findings were observed in the other seven cortical ROI (Figure3).
Using the extended model, the median α values differed significantly between some cortical ROI (Figure4), suggesting a potential association between the additional parameters incorporated in the time-fractional order Bloch equations and the effect of tissue constituents on magnetization relaxation in MRF signals.

Conclusions

The extended time-fractional order Bloch equations achieved more accurate MRF signal fitting across ten cortical ROI, which was not achievable using the MRF dictionary generated by Magin’s and the classical models.
Anomalous relaxation models have the potential to extract additional information from MRF signals to describe the architectonic variability between cortical regions more accurately, leading to more accurate cortical parcellation in individuals.

Acknowledgements

This research was conducted at the Australian Research Council Training Centre for Innovation in Biomedical Imaging Technology (IC170100035) and funded by the Australian Government. The authors also acknowledge the facilities and scientific and technical assistance of the National Imaging Facility, a National Collaborative Research Infrastructure Strategy (NCRIS) capacity, at the Centre for Advance Imaging, The University of Queensland.

References

1. Honey, C. J.; Thivierge, J.-P.; Sporns, O., Can structure predict function in the human brain? Neuroimage 2010, 52 (3), 766-776.

2. Lebel, C.; Walker, L.; Leemans, A.; Phillips, L.; Beaulieu, C., Microstructural maturation of the human brain from childhood to adulthood. Neuroimage 2008, 40 (3), 1044-55.

3. Rose, S. E.; Janke, A. L.; Chalk, J. B., Gray and white matter changes in Alzheimer's disease: a diffusion tensor imaging study. J Magn Reson Imaging 2008, 27 (1), 20-6.

4. Awad, I. A.; Rosenfeld, J.; Ahl, J.; Hahn, J. F.; Luders, H., Intractable epilepsy and structural lesions of the brain: mapping, resection strategies, and seizure outcome. Epilepsia 1991, 32 (2), 179-86.

5. Duffau, H., Brain mapping: from neural basis of cognition to surgical applications. Springer Science & Business Media: 2011.

6. Cohen-Adad, J.; Polimeni, J. R.; Helmer, K. G.; Benner, T.; McNab, J. A.; Wald, L. L.; Rosen, B. R.; Mainero, C., T2* mapping and B0 orientation-dependence at 7 T reveal cyto-and myeloarchitecture organization of the human cortex. Neuroimage 2012, 60 (2), 1006-1014.

7. Does, M. D., Inferring brain tissue composition and microstructure via MR relaxometry. Neuroimage 2018, 182, 136-148.

8. Geyer, S.; Weiss, M.; Reimann, K.; Lohmann, G.; Turner, R., Microstructural parcellation of the human cerebral cortex - from Brodmann's post-mortem map to in vivo mapping with high-field magnetic resonance imaging. Front Hum Neurosci 2011, 5.

9. Tardif, C. L.; Dinse, J.; Schäfer, A.; Turner, R.; Bazin, P.-L. In Multi-modal surface-based alignment of cortical areas using intra-cortical T1 contrast, International Workshop on Multimodal Brain Image Analysis, Springer: 2013; pp 222-232.

10. Cercignani, M.; Bouyagoub, S., Brain microstructure by multi-modal MRI: Is the whole greater than the sum of its parts? Neuroimage 2018, 182, 117-127.

11. Marques, J. P.; Khabipova, D.; Gruetter, R., Studying cyto and myeloarchitecture of the human cortex at ultra-high field with quantitative imaging: R-1, R-2 and magnetic susceptibility. Neuroimage 2017, 147, 152-163.

12. Stuber, C.; Morawski, M.; Schafer, A.; Labadie, C.; Wahnert, M.; Leuze, C.; Streicher, M.; Barapatre, N.; Reimann, K.; Geyer, S.; Spemann, D.; Turner, R., Myelin and iron concentration in the human brain: A quantitative study of MRI contrast. Neuroimage 2014, 93, 95-106.

13. Edwards, L. J.; Kirilina, E.; Mohammadi, S.; Weiskopf, N., Microstructural imaging of human neocortex in vivo. Neuroimage 2018, 182, 184-206.

14. Ma, D.; Gulani, V.; Seiberlich, N.; Liu, K.; Sunshine, J. L.; Duerk, J. L.; Griswold, M. A., Magnetic resonance fingerprinting. Nature 2013, 495 (7440), 187-92.

15. Moeiniyan Bagheri, S.; Vegh, V.; Reutens, D., Magnetic Resonance Fingerprinting (MRF) can reveal microstructural variations in the brain gray matter. 2018.

16. Qin, S.; Liu, F.; Turner, I. W.; Yu, Q.; Yang, Q.; Vegh, V., Characterization of anomalous relaxation using the time-fractional Bloch equation and multiple echo T2 *-weighted magnetic resonance imaging at 7 T. Magn Reson Med 2017, 77 (4), 1485-1494.

17. Magin, R. L.; Li, W.; Pilar Velasco, M.; Trujillo, J.; Reiter, D. A.; Morgenstern, A.; Spencer, R. G., Anomalous NMR relaxation in cartilage matrix components and native cartilage: fractional-order models. J Magn Reson 2011, 210 (2), 184-91.

Figures

Figure 1 Pseudo-randomised MRF acquisition patterns. The flip angle varies between 0° and 80° in a sinusoidal pattern and the repetition time ranges from 80ms to 90ms in a Perlin noise pattern.

Figure 2 MRF dictionary matching accuracy between classical monoexponential Bloch equations (left box), Magin et al model (middle box), and extended Bloch equations (right box) in cortical aeras 2, 4 and 6 was compared using a) dot product of the actual and best matching MRF signals, and b) mean squared error of MRF residuals. Note that outliers more than three median absolute deviations (MAD) are removed.

Figure 3 MRF dictionary matching accuracy between classical monoexponential Bloch equations (left box), Magin et al model (middle box), and extended Bloch equations (right box) in cortical aeras 7A, 7P, 7PC, 5L, 5M, 5Ci, and hIP3 was compared using a) dot product of the actual and best matching MRF signals, and b) mean squared error of MRF residuals. Note that outliers more than three median absolute deviations (MAD) are removed.

Figure 4 Distribution of time-fractional order parameter α values was compared across ten cortical areas of interest; a) areas 2, 4, and 6, b) areas 7A, 7P, 7PC, 5M, 5L, 5Ci, and hIP3.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1538