Purpose

Spin-lattice relaxation rates in the rotating frame (R_1ρ=1/T_1ρ) measured by spin-lock methods at low locking amplitudes (w₁) are sensitive to the effects of water diffusion in intrinsic gradients and may provide information on tissue microvasculature^1,2, but accurate estimates are challenging in the presence of B₀ and B₁ inhomogeneities. Although composite pulse preparations (90_x-τ_y/2-180_y-τ_-y/2-90_x) have been developed to compensate for non-uniform fields³, there are residual image artifacts and errors in quantification of R_1ρ and their dispersion at low w₁. Here, we analyzed the source of these errors and developed an approximate theoretical analysis that provides a means to correct them.

Methods

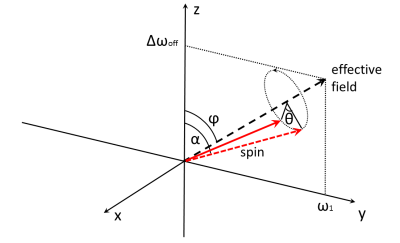
When ω₁ is comparable to a local B₀ shift (Δω_off), the magnetization nutates about the effective field. When there is also a B₁ imperfection, the nominal 90° excitation pulse rotates the magnetization to a zenith angle of only α = β·π/2, in which β is the ratio of the actual flip angle to the nominal flip angle. Fig. 1 shows the nutation of the magnetization about the effective field at angle = θ to the effective field. The effective field itself has a zenith angle of φ and an amplitude of ω_{1_eff}, $$φ=tan^{-1}(\omega_1/\Delta\omega_{off})$$ (1) $$\omega_{1\_eff}=\sqrt{\omega_1^2+\Delta\omega_{off}^2}$$ (2)
In spin-lock imaging after the composite preparation cluster, the magnetization nutates back into the transverse plane, in which case image artifacts are reduced. However, a portion of the magnetization is not in the transverse plane during the preparation period, and so does not experience R_1ρ decay, and subsequently causes errors in the quantification of R_1ρ. Here, we simply separate the magnetization after the first 90_x excitation pulse into two components: a transverse component which experiences R_1ρ decay, and a residual longitudinal component. The transverse component (f_⏊) can be calculated as the average of the projection of magnetization onto the transverse plane with θ varying from 0 to θ_τ/2=2π·τ/2·ω_{1_eff} (τ = the spin-lock time) and assuming no R_1ρ decay,
$$ f_⏊(\theta)=\frac{\int_{0}^{\theta_{\tau/2}}\sqrt{(\sin(\alpha-φ)\cdot\sin(\theta))^2+(\mid\cos(\alpha-φ)\sin(φ)\mid+\mid\sin(\alpha-φ)\cos(φ)\mid\cos(\theta))^2}d\theta}{\theta_{\tau/2}}$$ (3)
The residual longitudinal component will experience relatively slow R₁ recovery. If there are no R_1ρ or R₁ decays, the spin-lock signal after the composite pulse preparation would approximately be the sum of signals from these two components. Assuming the magnetization is 1, the residual longitudinal component is then 1 - f_⏊. When there are R_1ρ and R₁ decays, the spin-lock signal after the composite pulse preparation is approximately these two components modified by relaxation. By assuming R_1ρ>>R₁ and rewriting f_⏊(θ) with f_⏊(τ), the normalized spin-lock signal in the presence of B₀ and B₁ shifts (S_off) can then be described by,
$$\frac{S_{off}(\tau)}{S_0}\approx f_⏊(\tau)exp(-R_{1\rho}\tau)+1-f_⏊(\tau)$$ (4)
R_1ρ can be obtained by fitting S_off/S₀ to Eq. (4).
We evaluated this correction approach through both simulations of the Bloch equations and experiments on a healthy human subject. Simulations were performed of both a single-pool and a two-pool model of tissue water. The two-pool system was used to mimic self-diffusion with pool A representing water molecules that do not experience any intrinsic gradients and pool B representing water molecules that diffuse through intrinsic gradients. Self-diffusion through intrinsic gradients alters the signal similarly to proton exchange between environments with different resonance frequencies. Spin-lock images were acquired at 3T with a TSE readout and with τ of 2, 12, 22, 32, 43, 52, 62, and 72ms, and w₁ of 0, 20, 50 and 100Hz. A B₀ map was obtained by two images acquired with a TFE sequence with TEs of 2.14ms and 5.34ms, TR of 7.35ms, and flip angle 30º. A B₁ map was obtained by two images acquired with TSE sequence with excitation flip angles of 80º and 160º, TR of 677ms, and TE of 10ms. All images were acquired with a 32-channel head coil on a 3T Philips scanner with an image resolution of 1×1×4mm.

Results

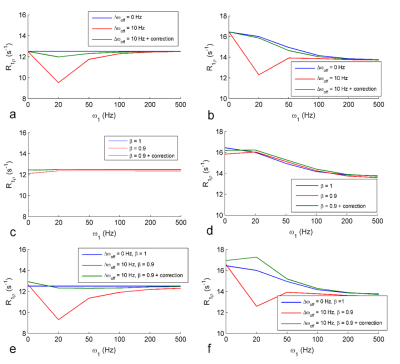
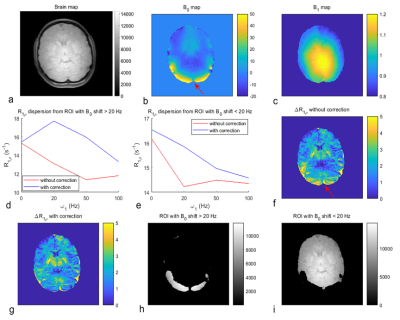
Fig. 2 shows the simulated R_1ρ dispersions with a B₀ shift, a B₁ error, and both B₀ and B₁ shifts, with and without correction. Note in Fig. 2e and 2f that the artifact can be reduced by using the correction approach. Also note that there are artifacts in the presence of a B₀ shift, but not a B₁ shift, suggesting the source of the artifact is mainly B₀ offsets. Fig. 3 shows images acquired from a healthy human subject. Note in Fig. 3b that there are severe B₀ shifts in the region indicated by the red arrow. Note in Fig. 3d that the artifact from this region is not corrected, especially at low w₁ (i.e. 20 and 50 Hz). In contrast, the artifact from ROIs with small B₀ shift in Fig. 3e can be corrected at low w₁. Although the R_1ρ dispersion from the region of large B₀ shift cannot be corrected with ω₁ of 20 and 50 Hz, it is corrected at 100 Hz. Fig. 3f and 3g show maps of ΔR_1ρ, the subtraction of two ΔR1ρ images acquired with ω₁ of 0 and 100Hz, without and with correction, respectively. Note that the artifact in Fig. 3f (red arrow) is reduced in Fig. 3g.

Discussion and Conclusion

The R_1ρ artifact at low w₁ can be reduced using this correction approach when there are small B₀ shifts.

Acknowledgements

No acknowledgement found.