1471
Accelerating T1Ρ mapping using patch-based low-rank tensor1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
Synopsis
T1ρ mapping requires the acquisition of multiple T1ρ-weighted images with different spin lock times to obtain the T1ρ maps, resulting in a long scan time. Compressed sensing has shown good performance in fast quantitative T1ρ mapping. In this study, we used a patch-based low-rank tensor imaging method to reconstruct the T1ρ-weighted images from highly undersampled data. Preliminary results show that the proposed method achieves a 6-fold acceleration and obtains more accurate T1ρ maps than the existing methods.
Introduction
Compressed sensing (CS) based reconstruction methods have been successfully applied in quantitative T1ρ mapping to reduce the scan time. A variety of constrained reconstruction methods that utilize spatial and /or parametric characteristics of T1ρ-weighted image series such as low-rank and sparsity have demonstrated effectiveness in achieving fast T1ρ mapping through sparse sampling(1-4). In these methods, anatomical correlations in the parameter dimension on a global or local scale are exploited. Besides, the characteristic of signal evolution in T1ρ mapping exhibits a low-rank structure in the parameter dimension that can be exploited to further reduce the scan times. In this work, we propose a patch-based reconstruction method utilizing the low-rank tensor decomposition (PLANT) to exploit the correlations of images.Methods
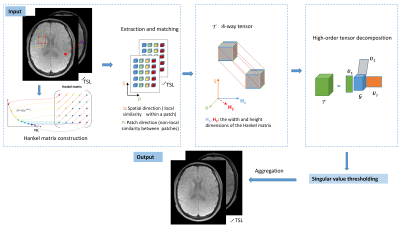
Figure 1 shows the flow diagram of the proposed method. Let $$$X\in C^{N_x \times N_y \times N_{TSL}}$$$ be the T1ρ-weighted image series to be reconstructed, where $$$N_x$$$ and $$$N_y$$$ are the number of voxels in the $$$k_x$$$ and $$$k_y$$$ dimension, and $$$N_{TSL}$$$ is the number of spin-lock times (TSLs). Due to the exponential decay, signals along the TSL dimension can be constructed as a Hankel Matrix. Then X can be expressed as a high‐order low‐rank representation on a patch scale, with respect to an appropriately chosen patch selection operator $$$P_p(\cdot)$$$. The image reconstruction problem can be modeled as the following optimization on the high-order low-rank tensor $$$\Gamma$$$ :$$\arg\min_{X}\frac{1}{2}||EX-Y||_F^2+\sum_p\lambda_p||\Gamma_p||_*\ \ \ \ s.t.\ \ \Gamma_p=P_p(X)\ \ \ \ \ [1]$$
where $$$||\cdot||_F$$$ is the Frobenius norm; $$$E$$$ is the encoding operator (5,6); $$$X$$$ is the image series to be reconstructed; $$$Y$$$ is the acquired k-space data; $$$||\cdot||_*$$$ is the nuclear norm; $$$\lambda_p$$$ is a regularization parameter; The patch selection operator $$$P_p(\cdot)$$$ forms a 4-way tensor from a patch centered at pixel $$$p$$$ from a set of T1ρ-weighted images (7) . Equation (1) can be transformed into the following formulation using the Lagrangian optimization scheme:
$$\arg\min_{X,\Gamma,\alpha}\frac{1}{2}||EX-Y||_F^2+\sum_p\lambda_p||\Gamma_p||_*+\frac{\mu}{2}\sum_p||\Gamma_p-P_p(X)||_F^2-\sum_p<\alpha_p, \Gamma_p-P_p(X)>\ \ \ \ \ [2]$$
Where $$$\mu$$$ is the penalty parameter; $$$\alpha_p$$$ is the Lagrange multiplier. Equation 2 can be efficiently solved through operator‐splitting via alternating direction method of multipliers (ADMM) (8) by decoupling the optimization problem into three sub-problems:
Update on $$$X$$$:
$$L_1(X):=\arg\min_X\frac{1}{2}||EX-Y||_F^2+\frac{\mu}{2}\sum_p||\Gamma_p-P_p(X)||_F^2-\sum_p<\alpha_p, \Gamma_p-P_p(X)> \ \ \ \ \ [3]$$
The solution $$$X$$$ can be effectively solved using the Conjugate Gradient algorithm(9).
Update on $$$\Gamma$$$:
$$L_2(\Gamma):=\arg\min_{\Gamma} \sum_p\lambda_p||\Gamma_p||_*++\frac{\mu}{2}\sum_p||\Gamma_p-P_p(X)||_F^2-\sum_p<\alpha_p, \Gamma_p-P_p(X)>\ \ \ \ \ [4]$$
The above problem can be solved using a high-order singular value decomposition (HOSVD) method. Similar image patches were grouped to form a 4-way tensor, which shows strong low multilinear rank structure and can be compressed using high-order tensor decomposition.
Update on $$$\alpha$$$:
$$\alpha_{n+1}=\alpha_n+P_p(X_{n+1})-\Gamma_{p, n+1}\ \ \ \ \ [5]$$
Evaluation
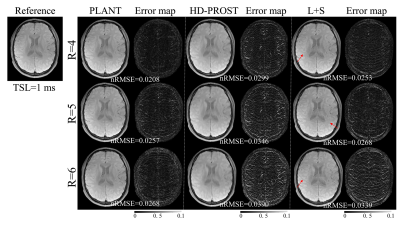
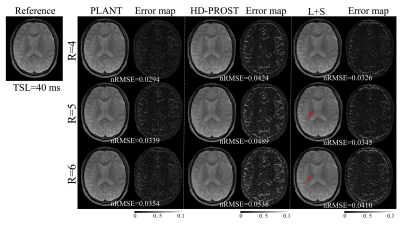
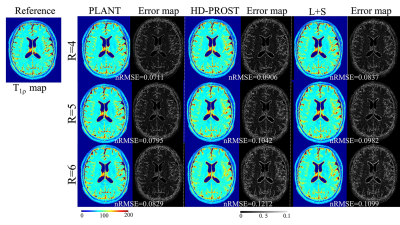
All MR data were acquired on a 3T scanner (Trio, SIEMENS, Germany) using a twelve-channel head coil. 2 healthy volunteers ( male, age 24±2) were recruited (IRB proved). Each volunteer was scanned using a spin-lock embedded turbo spin-echo (TSE) sequence (9). Imaging parameters were: TR/TE=4000ms/9ms, spin-lock frequency 500 Hz, echo train length 16, FOV=230mm2, matrix size=384×384, slice thickness 5mm, and TSLs=1, 20, 40, 60, and 80ms. The acquired k-space data were retrospectively undersampled along the ky dimension with a pseudo-random undersampling acquisition scheme (10) with net acceleration factors R=4, 5, and 6. T1ρ-weighted images were reconstructed by the SCOPE method, the HD-PROST method (11), and the L+S method (5), respectively. The quality of the reconstructed images and the estimated T1ρ maps were assessed by normalized root mean square error (nRMSE) as follows:$$\text{nRMSE}=\sqrt{||x_{est}-x_{ref}||_2^2/||x_{ref}||_2^2}\ \ \ \ \ [6]$$
where $$$x_{est}$$$ denotes the reconstructed image or the estimated T1ρ map from the undersampled data, and $$$x_{ref}$$$ is the reference image or T1ρ map from the fully sampled k-space data.
Results
Figure 2 and Figure 3 show the T1ρ-weighted images at different TSLs reconstructed using the SCOPE method, the HD-PROST method, and the L+S method with R=4, 5, and 6. The corresponding error maps are also shown for comparison. It can be seen that the reconstruction using L+S has visible undersampling artifacts, and HD-PROST reconstruction shows blur artifacts, while the proposed PLANT reconstruction only exhibits negligible artifacts. The T1ρ-weighted images from PLANT show the lowest error. The derived T1ρ maps using PLANT are more accurate than the other two methods with the lowest nRMSE (Figure 4).Conclusion
The proposed method offers better performance than the existing methods in retrospective experiments and can significantly reduce the scan time of T1ρ mapping. This technique might help facilitate fast T1ρ mapping in clinics.Acknowledgements
This work is supported in part by the National Natural Science Foundation of China under grant nos. 61771463,81971611, National Key R&D Program of China nos. 2020YFA0712202, 2017YFC0108802References
1. Zhu Y, Zhang Q, Liu Q, Wang YX, Liu X, Zheng H, Liang D, Yuan J. PANDA- T1ρ: Integrating principal component analysis and dictionary learning for fast T1rho mapping. Magn. Reson. Med., 2015;73(1):263-272.
2. Zhou Y, Pandit P, Pedoia V, Rivoire J, Wang Y, Liang D, Li X, Ying L. Accelerating T1ρ cartilage imaging using compressed sensing with iterative locally adapted support detection and JSENSE. Magn. Reson. Med., 2016;75(4):1617-1629.
3. Pandit P, Rivoire J, King K and Li X. Accelerated T1ρ acquisition for knee cartilage quantification using compressed sensing and data-driven parallel imaging: A feasibility study Magn. Reson. Med., 2016;75 1256-6.
4. Zibetti M V W, Sharafi A, Otazo R and Regatte R R , Accelerating 3D- T1ρ mapping of cartilage using compressed sensing with different sparse and low rank models. Magn. Reson. Med., 2018;80(4):1475-1491.
5. Otazo R, Candes E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn. Reson. Med .,2015;73(3):1125-1136.
6. Pruessmann K P, Weiger M, Bornert P and Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn. Reson. Med., 2001; 46:638-51.
7. Akçakaya M, Basha TA, Goddu B, et al. Low‐dimensional structureself‐learning and thresholding: regularization beyond compressed sensing for MRI reconstruction. Magn Reson Med.2011;66:756–767.
8. Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn. 2011;3:1–122.
9. Hestenes MR, Stiefel E. Methods of conjugate gradients for solving linear systems. J Res Natl Bur Stand. 1952;49:409.
10. Rich A, Gregg M, Jin N, Liu Y, Potter L, Simonetti O, Ahmad R. CArtesian sampling with Variable density and Adjustable temporal resolution (CAVA). Magn Reson Med 2020;83(6):2015-2025.
11. Bustin A, Lima da Cruz G, Jaubert O, Lopez K, Botnar RM, Prieto C. High-dimensionality undersampled patch-based reconstruction (HD-PROST) for accelerated multi-contrast MRI. Magn Reson Med 2019;81(6):3705-3719.
Figures