1421
The Impact of Quasi-Transverse Electric Modes Excited by Dipole Antennas on Transmit Field in In Vivo Ultrahigh Field MRI
Daniel Wenz1,2 and Rolf Gruetter1,3
1CIBM Center for Biomedical Imaging, Lausanne, Switzerland, 2Animal Imaging and Technology, Ecole Polytechnique Federale de Lausanne (EPFL), Lausanne, Switzerland, 3Laboratory of Functional and Metabolic Imaging (LIFMET), Ecole Polytechnique Federale de Lausanne (EPFL), Lausanne, Switzerland
1CIBM Center for Biomedical Imaging, Lausanne, Switzerland, 2Animal Imaging and Technology, Ecole Polytechnique Federale de Lausanne (EPFL), Lausanne, Switzerland, 3Laboratory of Functional and Metabolic Imaging (LIFMET), Ecole Polytechnique Federale de Lausanne (EPFL), Lausanne, Switzerland
Synopsis
This work investigates quasi-transverse electric modes which can be excited within rectangular dielectric blocks which are often used to shorten dipole antennas for MRI at 7T. In simulations we studied different parameters which can affect the performance of a dielectrically-shortened dipole antenna. We showed that an optimal geometry for the case when the block and the sample are physically separated differs significantly from the case when perfect direct contact is achieved. Two prototypes were built and used in an in vivo MRI experiments involving one subject showing how different dielectric modes can affect the image quality.
Introduction
Dipole antennas can provide significant transmit field (B1+) efficiency and SNR gains in UHF-MRI1,2. One promising approach to shorten dipole antennas (~50cm at 297.2MHz in free space) is to use a high-εr medium3-9. The dimensions of dielectric blocks used previously were rather large, which made it difficult to use them in large dipole antenna arrays. Those studies followed what Raaijmakers et al. suggested3, and what they investigated later4 showing that optimal B1+ efficiency can be achieved for a block with (150x50x50)mm3 and εr between 90 and 110. Both of these reports3,4 focused on the special case where there was direct contact between the block and the human body. Yet such contact is rather difficult to achieve for a solid, rectangular geometry, and it may not always be feasible in clinical settings (especially for e.g. human head). Therefore, it is reasonable to assume that the dielectric block and the anatomical structure are physically separated. In previous work, we observed that certain types of dielectrically-shortened dipole antennas produced an efficient B1+ in the presence of a small air gap while others did not10. We hypothesized that different dielectric modes11,12 can be induced within the rectangular block, thereby affecting antenna performance. Therefore, the aim of the present study was to investigate the influence of rectangular block geometry, dielectric permittivity and antenna/subject physical separation on the B1+ produced by dielectrically-shortened dipole antennas suitable for MRI at 7T and to determine how they influence in vivo experiments.Methods
Electromagnetic field simulations were performed using Sim4Life (Sim4Life,Switzerland). Two phantoms were used: a spherical one (radius=85mm, εr=50.6, σ=0.66S/m), and a cuboid one ((300x300x300)mm3, εr=34, σ=0.47S/m). We used B1+ efficiency defined as: B1+/√Pin , where Pin is input power, and SAR efficiency defined as B1+/√SAR10g, where SAR10g is maximum SAR averaged over 10g. B1+ distribution within the spherical phantom was studied for different rectangular block geometries (Fig.1) and different values of εr (35,50,80,100,150,200,300,500), assuming a 5-mm air gap between the block and the phantom. The dimension a (a0) was constant for each εr value: 35(242mm), 50(202mm), 80(160mm), 100(144mm), 150(118mm), 200(102mm), 300(84mm) and 500(64mm). One constant geometry (160x60x7.5)mm3 of the block was used to compare B1+ efficiency for different εr. The effect of an air gap (1,2,3,4,5mm) on B1+ distribution in a cuboid phantom was studied for one larger block (0.75b0, d/b=0.75) for each εr. The cutoff frequency of each quasi-transverse electric (TE) mode was determined from: $$$f_{cutoff}=\frac{c}{2\pi\epsilon_{r}}\sqrt{\left(\frac{m\pi}{a}\right)^{2}+\left(\frac{n\pi}{b}\right)^{2}+\left(\frac{l\pi}{d}\right)^{2}}$$$ where c is the velocity of light; m,n,l are the dielectric mode indices (Fig.1). Two dielectrically-shortened dipole antennas (εr=80) were designed, built and evaluated in MR experiments: (160x70x52.5)mm3 and (160x70x17.5)mm3. MR experiments were conducted in one male subject in three different regions of interest (head,calf,wrist) using a 7T-68cm bore scanner (Siemens,Germany). MR experiments were conducted using gradient echo (GRE) imaging. For in vivo experiments, deionized water was replaced by D2O.Results
B1+ distribution within the spherical phantom for d=0.125b (b=0.5b0 and b=0.75b0) resulted in the highest B1+ efficiency in the center of the phantom for all εr. The most apparent change in B1+ and decreased efficiency was observed for d=0.75b (b=b0, b=0.75b0 and b=0.5b0) for all εr and for blocks with d=0.5b (especially for higher εr -Fig.1). For the constant block geometry (160x60x7.5)mm3 the highest transmit field efficiency in the center of the spherical phantom was obtained with εr=300 and εr=200 (Fig.2). For lower εr (35,50), despite the air gap, the B1+ pattern was very similar to the one obtained with direct contact between the block and the cuboid phantom, while for higher εr a significant difference in B1+ pattern and efficiency could be observed (Fig.3). The mode excited in the larger block (d=0.75b) was interpreted as $$$TE_{1\delta\delta}^y$$$ and the one in the smaller block (d=0.25b) as $$$TE_{11\delta}^z$$$ (Fig.4). The thinner block provided highly superior in vivo image quality for all tissues compared to its thicker counterpart, which yielded very noisy images (very low to no SNR - Fig.5).Discussion and Conclusion
This study demonstrates for the first time why different types of dielectrically-shortened dipole antennas can produce (in)efficient B1+ in an in vivo UHF-MRI experiment. We showed that the different types of dielectric modes ($$$TE_{11\delta}^z$$$ and $$$TE_{1\delta\delta}^y$$$) that can be excited within the block had a crucial impact on the resulting B1+. Dielectric blocks in which the $$$TE_{11\delta}^z$$$ mode was allowed to propagate performed better in terms of B1+ and SAR efficiency than their smaller counterparts, for which the $$$f_{cutoff}$$$ was well above the resonance frequency of protons at 7T. Reducing the block thickness (d=0.125b) is advantageous in the context of B1+ distribution and efficiency for all εr values. Higher-order mode $$$TE_{12\delta}^z$$$, which was induced in higher-εr blocks, provided significantly higher B1+ efficiency than $$$TE_{11\delta}^z$$$, which propagated in lower-εr blocks for a given block geometry (160x60x7.5)mm3. We observed that the block/subject physical separation and loading geometry are critical to understand why some dielectric blocks in which $$$TE_{1\delta\delta}^y$$$ is expected to propagate produced rather efficient B1+ while others did not. In vivo experiments showed that $$$TE_{1\delta\delta}^y$$$ mode, unlike $$$TE_{11\delta}^z$$$, led to substantially degraded image quality, highlighting the influence of dielectric block geometry and propagation of dielectric modes on the performance of dielectrically-shortened dipole antennas.Acknowledgements
We acknowledge access to the facilities and expertise of the CIBM Center for Biomedical Imaging, a Swiss research center of excellence founded and supported by Lausanne University Hospital (CHUV), University of Lausanne (UNIL), Ecole polytechnique fédérale de Lausanne (EPFL), University of Geneva (UNIGE) and Geneva University Hospitals (HUG).References
1. Raaijmakers AJE, et al. The fractionated dipole antenna: A new antenna for body imaging at 7 Tesla. Magn Reson Med (2016).2. Lattanzi R et al. Approaching ultimate intrinsic signal-to-noise ratio with loop and dipole antennas. Magn Reson Med (2018).
3. Raaijmakers AJE, et al. Design of a radiative surface coil array element at 7 T: the single-side adapted dipole antenna. Magn. Reson. Med (2011).
4. Ipek O, et al. Optimization of the radiative antenna for 7-T magnetic resonance body imaging,” Concepts Magn. Reson. Part B Magn. Reson. Eng (2013).
5. Winter L, et al. Design and Evaluation of a Hybrid Radiofrequency Applicator for Magnetic Resonance Imaging and RF Induced Hyperthermia: Electromagnetic Field Simulations up to 14.0 Tesla and Proof-of-Concept at 7.0 Tesla. Plos One (2013).
6. Sanchez JD, et al., Radiative MRI coil design using parasitic scatterers: MRI Yagi. IEEE Transactions on Antennas and Propagation (2018).
7. Woo MK et al., Improved B1+ efficiency of a dipole antenna equipped with high dielectric constant (HDC) materials at 10.5T. Proc. Intl. Soc. Mag. Reson. Med. 28 (2019).
8. Sadeghi-Tarakameh A et al., “A New Coil Element for Highly-Dense Transmit Arrays : An Introduction to Non-Uniform Dielectric Substrate (NODES) Antenna. Proc. Intl. Soc. Mag. Reson. Med. 28 (2019).
9. Oberacker E et al., Radiofrequency applicator concepts for thermal magnetic resonance of brain tumors at 297 MHz (7.0 Tesla). Int. J. Hyperthermia (2020).
10. Wenz D and Gruetter R, Dielectrically-Shortened Dipole Antennas for MRI at 7.0 T: Thick or Thin? Proc. Intl. Soc. Mag. Reson. Med. 28 (2020).
11. Aussenhofer SA and Webb AG, Design and evaluation of a detunable water-based quadrature HEM 11 mode dielectric resonator as a new type of volume coil for high field MRI: Design and Evaluation of a Detunable Quadrature HEM 11. Magn. Reson. Med (2012).
12. O’Reilly T, et al. Modular transmit/receive arrays using very-high permittivity dielectric resonator antennas: Very-High Permittivity DRA Arrays. Magn Reson Med (2018).
Figures
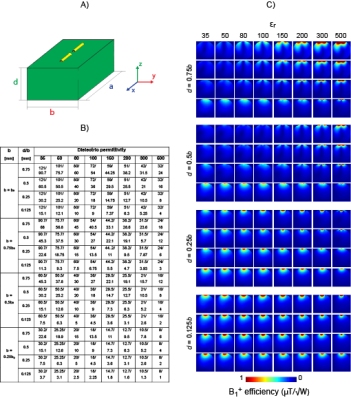
Fig. 1. A) The frame of reference used to determine
the type of dielectric mode (transformation
to the MRI frame of reference: x-z, y-x, z-y). B) The dimensions of
rectangular blocks from simulations, C) B1+ distribution
in the spherical phantom for the geometries from B) and different εr. The figure was divided into four groups (d/b=0.75, 0.5, 0.25, 0.125). Each group consists of four rows b/b0: 1, 0.75,
0.5, 0.25 (b0=a0/2). Substantial
differences in B1+ pattern and efficiency can be observed
between different geometries for given εr, as well as for the same a/b/d ratio, but different εr.
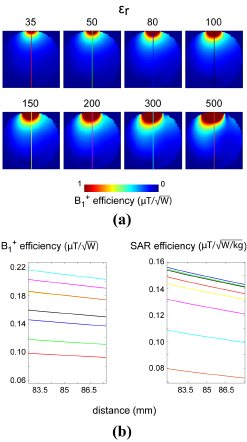
Fig. 2.
(a) B1+ distribution within the spherical phantom for the
constant block geometry (160x60x7.5)mm3 length as a function of εr (the
air gap = 5 mm). (b) Transmit and SAR efficiency as functions of distance. The
plots were zoomed in (85 mm on the x-axis corresponds to the center of the
phantom). The highest B1+ efficiency
in the center of the phantom was obtained for εr = 300 (0.210 μT/√W)
and εr = 200 (0.197 μT/√W), but at the cost
of reduced SAR efficiency (0.103 μT/√W/kg and 0.126 μT/√W/kg). Note that in higher-εr blocks (300, 500), a higher-order mode TE12δz was excited.
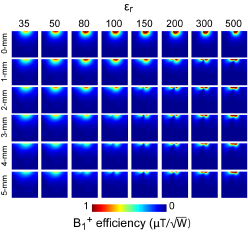
Fig. 3. B1+ distribution in the cuboid phantom as
a function of εr of the block and the
block/phantom physical separation. The
geometry of one of the larger blocks was chosen (b = 0.75b0, d/b
= 0.75 – Fig.1). The effect of different sizes of an air gap (1, 2, 3, 4, 5 mm)
was investigated for all εr values.
Note no significant change in B1+ pattern
for lower εr (35,
50) when the antenna was moved 5 mm away from the phantom. B1+ changed
significantly for higher εr. The
higher the εr of the
block, the lower was the “threshold” size of the air gap for which B1+ pattern
changed along with decreased efficiency.
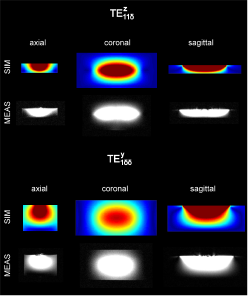
Fig. 4.
Visualization of dielectric modes: the comparison between the electromagnetic
field simulations and MR measurements for two elements: thinner one (d = 0.25b) and thicker one (d =
0.75b). GRE imaging was used
(TR/TE=8.6/4.0 ms, FOV=250 x
250 mm2, slice thickness = 7.0
mm, FA=15º, reference transmit voltage = 5 V). The simulations are in an
excellent agreement with the measurements and show significantly different
magnetic field distribution between the blocks. The mode that propagates within
the thinner block was interpreted as
TE11δz, and within the
thicker one as
TE1δδy.
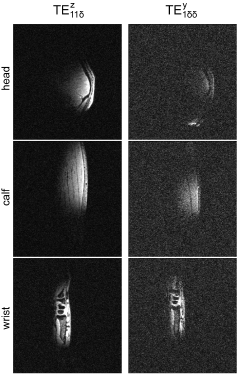
Fig. 5.
In vivo MRI experiments (3D-GRE:
TR/TE = 6.5/2.82ms, FOV = 256x240 mm2, slice thickness = 1.0 mm, FA = 4º,
reference transmit voltage = 100 V) in one human male subject using two blocks:
thinner (d/b = 0.25) and thicker one (d/b = 0.75). Three different regions of
interest (head, calf, wrist) were investigated. The quality of all of the
images was significantly compromised for the larger block (very noisy). The
overall quality of the images depended on the level of curvature of the
anatomical structure. The acquisition parameters of the RF pulse sequence were
used to scan each body part.