1412

Analysis of preamplifier decoupling effect in MRI coil array with electromagnetic field and RF circuit co-simulation

Ming lu^1,2, Bei Zhang³, John C. Gore^1,2, and Xinqiang Yan^1,2
¹Vanderbilt University Institute of Imaging Science, Vanderbilt University Medical Center, Nashville, TN, United States, ²Department of Radiology and Radiological Sciences, Vanderbilt University Medical Center, Nashville, TN, United States, ³Advanced Imaging Research Center, University of Texas Southwestern Medical Center, Dallas, TX, United States

Synopsis

Preamplifier decoupling is a standard way of suppressing inter-element inductive coupling in MRI receive arrays. A well-known method to evaluate and optimize RF coils before practical fabrication is to use circuit-level and electromagnetic (EM) field-level simulations. However, to be best of our knowledge, currently there is not a solid method to evaluate the preamp decoupling effect with circuitry and EM field analysis. In this work, we used RF circuit and EM co-simulation4 to evaluate the preamplifier decoupling effect and tested it on the conventional coil (LIC) and the recently introduced high impedance coil (HIC).

Purpose:

Preamplifier decoupling is a standard way of suppressing inter-element crosstalk in MRI receive arrays. The original preamplifier decoupling was mainly used to reduce the coupling among non-adjacent elements in which the geometrically-overlap decoupling¹ is not feasible. Recently, a strong trend has been arising to develop advanced preamp decoupling methods for flexible coils. Unlike the original method in Roemer et al¹, advanced preamp decoupling methods are aiming at robust decoupling/noise suppression so the overlapping area is not crucial^2,3. A well-known method to evaluate and optimize RF coils before practical fabrication is to use circuit-level and electromagnetic (EM) field-level simulations. However, to be best of our knowledge, currently there is not a solid method to evaluate the preamp decoupling effect with circuitry and EM field analysis. In this work, we used RF circuit and EM co-simulation⁴ to evaluate the preamplifier decoupling effect and tested it on the conventional coil (LIC)¹ and the recently introduced high impedance coil (HIC)².

Methods:

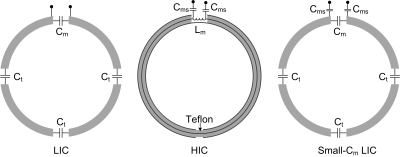
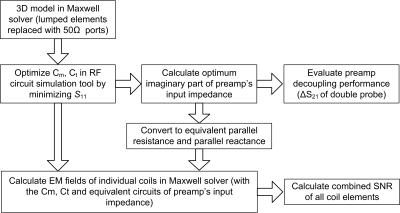
Figure 1 showed the schematic drawings of the LIC and HIC. For the LIC, we evaluated two matching strategies, one is the parallel matching strategy with a single matching capacitor C_m, and the other one is the series matching strategy with two series capacitors (C_ms) and an intentional small capacitor C_m (referred to as small-C_m LIC). The small C_m is expected to improve the quality factor of the blocking circuit consisting C_m and the preamplifier load^5-7. In each case, the coil has a diameter of 78 mm, and was tuned at 128 MHz and matched to 50 Ω.

Figure 2 depicted the procedures of the proposed co-simulation approach. First, coils were modeled in an EM simulation (Ansys HFSS) with all lumped elements replaced with 50 Ω. Second, values of tuning and matching capacitors were optimized by minimizing coils’ reflection coefficient (S₁₁) in co-simulation environment (Ansys Designer). Third, the imaginary part of the preamplifier's input impedance was optimized to maximize the preamplifier decoupling. Similar to the practical case⁸, this was obtained by minimizing the transmission coefficient (S₂₁) of a well-decoupled double-pick-up probe that was placed several centimeters above the coil. By now, the preamplifier decoupling ability can be evaluated in the RF circuit simulator. To further evaluate the SNR performance, the optimized imaginary part and the previously set Re[Z_in] were converted to equivalent parallel resistance (R_eq) and parallel reactance (usually inductance, L_eq) and imported into EM simulation. Finally, individual B₁^- fields and electric (E-) fields were calculated and exported to MATLAB for SNR calculation. Unlike the conventional simulations assuming other coils opened, this simulation method will account for additional noise correlation and SNR loss caused by residual coupling.

Results and Discussions:

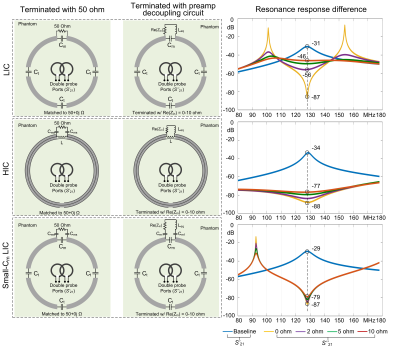
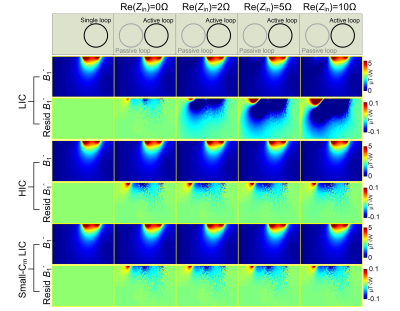
Figures 3 showed the preamplifier decoupling effect of the three coils, with Re[Z_in] set with 0, 2, 5 and 10 Ω. Similar to the practical case, the preamplifier decoupling effect was evaluated as the resonate response difference (ΔS₂₁) between the 50 Ω termination and the preamplifier input impedance termination8. For Re[Z_in] = 0 Ω, almost perfect decoupling can be achieved, with ΔS₂₁ of ~58 dB. As Re[Z_in] increases, ΔS₂₁ of LIC coil with normal Cm dropped dramatically, with ΔS₂₁=25/18/15 dB when Re[Z_in] =2/5/10 Ω respectively. On the contrary, both the HIC coil and the small-C_m LIC varied much less when the Re[Z_in] changed. For the HIC, the ΔS₂₁=50/45/43 dB when Re[Z_in] =2/5/10 Ω. For the small-C_m LIC coil, the ΔS₂₁=56/53/50 dB when Re[Z_in] =2/5/10 Ω. It should be noted that choosing extremely small C_m in the series matching circuit of the LIC will induce a dipole mode to the loop coil, making the current distribution along conductors less uniform than that of the typical LIC coil.

Figure 4 showed the B₁^- field distortion due to non-perfect preamplifier decoupling. For each case, two coils were placed side-by-side with 2 mm apart. The coil on the right was driven with 1-watt power while the coil on the left was terminated with R_eq and L_eq. These B₁^-fields were also compared to the baseline B₁^- fields from a single coil (without the left coil, left column in Figure 4). The B₁^- results were consistent with the S₂₁ in Figure 3. For the typical LIC coil, the B₁^-distortion was highly dependent on the Re[Z_in]. For the HIC and small-C_m LIC coils, however, the original B₁^-field can be maintained even with Re[Z_in] = 10 Ω.

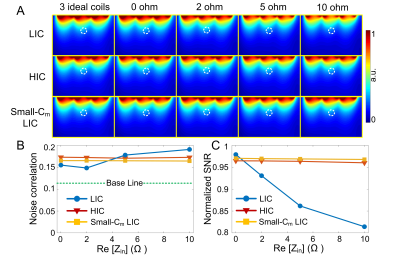
Figure 5A showed the normalized SNR maps from three side-by-side coils. Figure 5B plotted the average noise correlation of neighbor coils (i.e., left-middle and right-middle coils). Figure 5C plotted normalized SNR values in an 40-mm-deep region that is directly under the middle coil. The SNR result was also consistent with simulated decoupling (ΔS₂₁) and B₁^- results.

Conclusion:

We proposed an RF circuit and EM field co-simulation method that can evaluate the preamplifier decoupling in terms of the resonate response difference, receive sensitivity (B₁^-), and array SNR.

Acknowledgements

No acknowledgement found.

References

1. Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magnetic resonance in medicine. 1990 Nov;16(2):192-225.

2. Zhang B, Sodickson DK, Cloos MA. A high-impedance detector-array glove for magnetic resonance imaging of the hand. Nature biomedical engineering. 2018 Aug;2(8):570-7.

3. Vasanawala SS, Stormont R, Lindsay S, Grafendorfer T, Cheng JY, Pauly JM, Scott G, Guzman JX, Taracila V, Chirayath D, Robb F. Development and clinical implementation of next generation very light weight and extremely flexible receiver arrays for pediatric mri. arXiv preprint arXiv:1705.00224. 2017 Apr 29.

4. Kozlov M, Turner R. Fast MRI coil analysis based on 3-D electromagnetic and RF circuit co-simulation. Journal of magnetic resonance. 2009 Sep 1;200(1):147-52.

5. Zhu H. Imris Inc. Coil decoupling for an RF coil array. United States patent US 8,138,762. 2012 Mar 20.

6. Wiggins GC, Polimeni JR, Potthast A, Schmitt M, Alagappan V, Wald LL. 96‐Channel receive‐only head coil for 3 Tesla: design optimization and evaluation. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2009 Sep;62(3):754-62.

7. Hergt M, Oppelt R, Vester M, Reykowski A, Huber KM, Jahns K, Fischer H. Low noise preamplifier with integrated cable trap. In: Proceedings of the 15th Annual Meeting of ISMRM, Berlin, Germany, 2007 (Abstract 1037).

8. Reykowski A, Wright SM, Porter JR. Design of matching networks for low noise preamplifiers. Magnetic resonance in medicine. 1995 Jun;33(6):848-52.

Figures

Figure 1. Circuit diagrams of three types of coil. From left to right: conventional L/C coil (referred to as Low Impedance Coil here), High Impedance Coil that is driven at the open port of a coaxial resonator, conventional LIC but with intentionally small C_m.

Figure 2. Procedures of the proposed co-simulation method to analyze the preamp decoupling performance. In addition to the circuit level analysis that can evaluate the resonate response difference due to preamp decoupling, this co-simulation provides a way of analyzing receive sensitivity distortion and SNR loss due to the non-perfect preamp decoupling performance.

Figure 3. Circuit-level simulation results of the preamp decoupling abilities in different types of coil. This ability was evaluated by the resonate response difference between the termination of 50Ω and the termination of the preamp. The real part of the preamp (Re[Z_in]) was set with different values from 0Ω to 10Ω. In practice, Re[Z_in]< 5 Ω is recognized as an acceptable low-input impedance. For LIC, C_m=59.9 pF and C_t= 33.1pF. For HIC, L_m= 483.8 nH and C_ms= 7.1 pF. For small-C_m LIC coil, C_m = 5.5 pF, C_t = 1000 pF and C_ms = 7.1 pF.

Figure 4. Receive sensitivity (B₁^-) simulation results. The B₁^- distortion due to non-perfect preamp decoupling can be easily observed in the residual B₁^-field which was calculated by subtracting the B₁^- from a single loop coil.

Figure 5. SNR and noise correlation simulation results. A: Calculated SNR maps in the central transverse slice. B: Average noise correlation of neighbor coils (i.e., left-middle and right-middle coils). C: Calculated SNR values in an 8-cm-deep region that is directly under the middle coil.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1412