1396
Use of High - Permittivity Pads to enhance SNR and Transmit Efficiency in the Chest at 7T
Giuseppe Carluccio1,2 and Christopher Michael Collins1,3
1Radiology, Center for Advanced Imaging Innovation and Research (CAI2R), New York, NY, United States, 2Radiology, Bernard and Irene Schwartz Center for Biomedical Imaging, New York, NY, United States, 3Bernard and Irene Schwartz Center for Biomedical Imaging, New York, NY, United States
1Radiology, Center for Advanced Imaging Innovation and Research (CAI2R), New York, NY, United States, 2Radiology, Bernard and Irene Schwartz Center for Biomedical Imaging, New York, NY, United States, 3Bernard and Irene Schwartz Center for Biomedical Imaging, New York, NY, United States
Synopsis
High-Permittivity materials have been recently used to shape the B1 field distribution to enhance SNR and transmit efficiency. So far, these materials have been mainly applied to increase SNR in the head. In this work, through numerical simulations, we explore the possibility to use high-permittivity pads to improve the signal in the chest. The pads are positioned between the model of the coils (8 TEM transmit coils and 24 receive loops) and of the human body. Our simulations show that some improvement can be obtained by adding the pads to the coils.
Introduction
High-Permittivity Materials (HPM) can impact the distribution of the B1 electromagnetic field, and they are becoming popular because of their ability to enhance local SNR and transmit efficiency. The optimal design of HPM pads involves the determination of the best combination of permittivity, thickness and shape to provide the desired RF field distribution. The SNR and transmit efficiency enhancements have been measured both in simulations and in experiments for several field strengths, with most of the applications designed for brain scan applications, and some notable work within the torso HPM pads at 3T1, and with ceramic resonators at 7T2. For example, with an HPM helmet it was observed an average SNR increase in the head of approximately 21%3. In this work, we present two pads with two different thicknesses and permittivity values to be used near the chest. We will evaluate through electromagnetic simulations both the SNR and transmit efficiency increase of the two pads respect to the case when the coils are positioned without any HPM pad at the minimal distance from the body.Methods
The electromagnetic fields were computed with commercial software (xFDTD; Remcom). The resulting fields were post-processed with in-house scripts in Matlab (The Mathworks) to determine the SNR distribution and the transmit efficiency maps. The transmit fields were generated with an 8 channel stripline array (16 cm long), while the fields were received with an array of 24 rectangular loop coils (6 cm wide and 12 cm long) operating at 300 MHz (Modeled after coil by Virtumed; Minneapolis). The coils were in a clamshell arrangement in order to provide similar RF excitation and signal reception on both sides of the chest (Figure 1). The performance of two HPM pads having different thickness, 1.5 cm and 3 cm, were evaluated for different permittivity values, and compared to the case where no pad is used and the coil closer to the body. The pads were designed to be conformal to the coil arrays and positioned between the coils and the body (Figure 1). We have chosen an optimum permittivity value for the 1.5 cm pad, and another for the 3 cm pad. The optimum value has been determined to provide the best compromise between SNR and transmit efficiency improvement in the heart. For these two optimum permittivity values, SNR and transmit efficiency comparisons were performed by computing point by point ratios with respect to the case when no HPM pad is used.The electromagnetic simulations have been performed with the Duke human body model of the Virtual Family4 having a resolution of 5mm in each direction. The SNR was computed as $$SNR=\sqrt{\Psi*R^{-1}\Psi} [1]$$where Ψ is the sensitivity matrix, and R is the noise covariance matrix5. The matrix R is given by the sum of the noise covariance matrix related to the induced thermal noise Rs in the body, and the diagonal noise matrix Rc where each element corresponds to the power dissipated in the corresponding coil5. For each voxel of two orthogonal planes, respectively one axial plane and a coronal plane near the center of the chest, a maximum allowable local transmit efficiency is calculated with an analytical solution6 that gives that optimal driving currents of the transmit coils. For each location r, the transmit efficiency map is determined by computing the transmit field with the coils driven with optimal currents, and normalized to generate the same amount of dissipated power in the body.
Results
Figure 2 shows line plots representing the average SNR value in the heart (3D volume average) and average transmit efficiency maps in the heart (2D planar average for two orthogonal slices). According to these plots, we determined that the optimum value of permittivity for the 1.5 cm pad is equal to 100, and 60 for the 3 cm pad, which confirms that the determination of the permittivity of HPM pads is related to many factors such as the operating frequency and the geometry of the pad. For these two optimum permittivity values, SNR and transmit efficiency comparisons have been plotted in Figure 3. By analyzing the SNR distribution and the transmit efficiency maps for different permittivities, we could observe that while lower permittivity values provide a more uniform improvement, too high permittivity values tend to provide strong improvements only near the surfaces of the body. Specifically, for the 3 cm pad, we observed a significant degradation of the SNR in deeper tissues for permittivities higher than 100, while for the 1.5 cm pad a similar pattern could be observed for values higher than 150.We have also compared the performance of the coils when they are positioned at different distances (1.5 cm and 3 cm) from the body without using any HPM pad. No significant difference was observed among these solutions, with the closer coil providing stronger fields at the more external tissues, and the more distant coils providing stronger SNR in deeper tissues. Early investigations on local 10 grams SAR average show that locations where use of HPM pads provide a high transmit efficiency, some high local hotspots may be present. Examination of effects on max local SAR for different shimming configurations are ongoing.Acknowledgements
This work was supported by National Institutes of Health grant R01EB021277 and was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net) at the New York University School of Medicine, which is an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).References
- de Heer P, Bizino MB, Versluis MJ, Webb AG, Lamb HJ. Improved cardiac proton magnetic resonance spectroscopy at 3 T using high permittivity pads. Investigative radiology. 2016 Feb 1;51(2):134-8.
- Aussenhofer SA, Webb AG. An eight-channel transmit/receive array of TE01 mode high permittivity ceramic resonators for human imaging at 7 T. Journal of Magnetic Resonance. 2014 Jun 1;243:122-9.
- Lakshmanan K., Walczyk J., Rupprecht S., Lanagan MT, Yang QX, Brown R, Collins CM. Improved Brain Imaging with an Integrated High-Permittivity Material Head Array. In Proceedings of the SMRM & SMRT Virtual Conference & Exhibition, 2020, p. 4803.
- Christ A, Kainz W, Hahn EG, Honegger K, Zefferer M, Neufeld E, Rascher W, Janka R, Bautz W, Chen J, Kiefer B. The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Physics in Medicine & Biology. 2009 Dec;55(2):N23.
- Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magnetic resonance in medicine. 1990 Nov 1;16(2):192-225.
- Carluccio G, Collins CM, Erricolo D. A fast, analytically based method to optimize local transmit efficiency for a transmit array. Magnetic Resonance in Medicine. 2014 Jan;71(1):432-9.
Figures
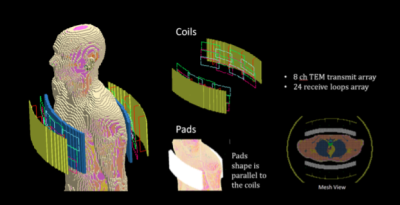
Geometry of the models of the coils and of the human body
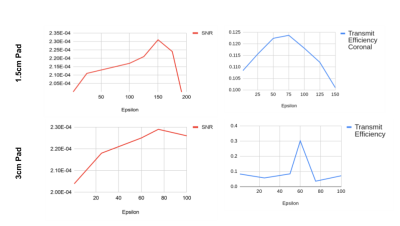
Plot of the average value of the SNR (red lines) and the transmit efficiency (blue lines) in the heart for different values of the permittivity for the two pads.
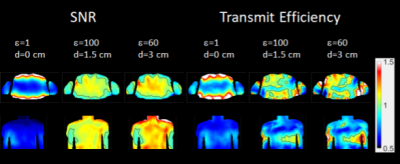
Plot of the distribution of the ratios of the SNR and Transmit Efficiency respect to the case where no pad is used, and the coils are positioned at minimal distance from the body.