Introduction

MRI is sensitive to motion due to its lengthy data acquisition that exceeds most types of physiological movement cycles [1]. Patient motion during scan can cause severe image artifacts and blurring. Acquiring extra data as navigator is one of the most popular motion correction method. Multiple navigator-based motion correction methods have been proposed [2-6]. Such approaches typically require significantly prolonged TE/TR [2, 3, 4, 5], non-Cartesian gradient waveforms [2, 3], or highly accurate extrapolation of coil sensitivity maps [6]. In short-TR sequences such as rapid GRE (Turbo-FLASH) and SSFP, there is not much idle time to insert long navigator echoes. Inspired by the self-navigated radial imaging [7-8], we propose a radial navigator (radNAV) approach, which is easily implemented with minimal increase in TE/TR and without the need for non-Cartesian gradients or coil sensitivity extrapolation. We demonstrate the feasibility of this approach to acquire motion information for image correction in turbo-FLASH sequences.

Methods

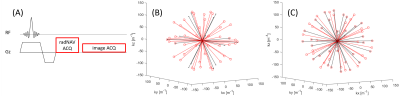
Data were acquired on a 3T MRI scanner (Prisma, Siemens AG, Erlangen, Germany) with a 20-channel head-neck coil and an ACR phantom (Newmatic Medical, Caledonia, MI). The turbo-FLASH sequence with radNAV was developed in-house with the Siemens IDEA environment. The radNAV spoke was acquired after excitation (Figure 1A) but before phase encoding and image acquisition. A single navigator frame is defined as a single temporal point consisted of multiple radNAV spokes grouped retrospectively. It is used for calculating motion amount at a given time point. The k-space trajectory of two example navigator frames consisted of sequential 15 and 30 evenly distributed spokes are demonstrated in Figure 1B.

The scanning parameters for the 3D turbo-FLASH with radNAV were: TR/TE = 5.5/3.4 ms, matrix size 128×128×96, voxel size 2mm isotropic, flip angle 8 degrees, readout bandwidth 700 Hz/px; the total time for full spokes of radNAV (including refocusing gradient of slab excitation, radNAV pre-phaser and readout) was 1.82 ms, with 100 readout points. In this study, 30 sequential spokes, evenly spatially distributed in space, constitute one radNAV frame, giving a 30×5.5 = 165 ms temporal resolution for the radNAV. Two image sets were acquired: one without any motion, and one with the phantom moved 3 times during the scan.

Image reconstruction and motion estimation/correction were performed in MATLAB (R2018b, MathWorks, MA, USA). After importing all radNAV signals, all the coil channels were combined using sum of complex raw data (SoR) method [9]. The first radNAV temporal frame was used as reference for motion estimation, and the motion amount along each spoke direction was calculated through a Gauss-Newton algorithm of a complex signal model [10]. The normalized unit vector along the r-th spoke (among total spoke number R) is defined as $$$\vec{n} = [n_{x,r}, n_{y,r}, n_{z,r}]$$$, where $$$n_{x}$$$, $$$n_{y}$$$ and $$$n_{z}$$$ are the vector components along $$$X$$$, $$$Y$$$ and $$$Z$$$ directions, which has an intuitive linear relation to the real motion amount $$$[\Delta x, \Delta y, \Delta z]$$$ in the 3D space:
$$\begin{bmatrix}
m_1 \\ m_2 \\ \vdots \\ m_R
\end{bmatrix}
=
\begin{bmatrix}
n_{x,1} & n_{y,1} & n_{z_1} \\
\vdots & \vdots & \vdots \\
n_{x,R} & n_{y,R} & n_{z_R}
\end{bmatrix}
\begin{bmatrix}
\Delta x \\
\Delta y \\
\Delta z
\end{bmatrix}
$$

Here $$$m_r$$$ represents the motion amount along spoke $$$r$$$ calculated by the Gauss-Newton algorithm. With a simple linear inversion, the motion amount of the current frame $$$[\Delta x, \Delta y, \Delta z]$$$ could be calculated.

The estimated motion vector $$$[\Delta x, \Delta y, \Delta z]$$$ was used to correct the acquired image during image reconstruction by transforming the motion-corrupted k-space signal $$$s$$$ into the corrected one $$$s_c$$$:
$$s_c(k_x,k_y,k_z) = s(k_x,k_y,k_z) e^{-j2 \pi (k_x\Delta x + k_y\Delta y + k_z\Delta z)}$$

Results

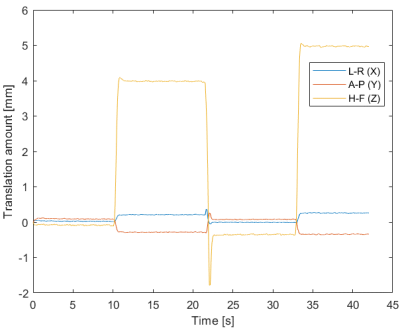
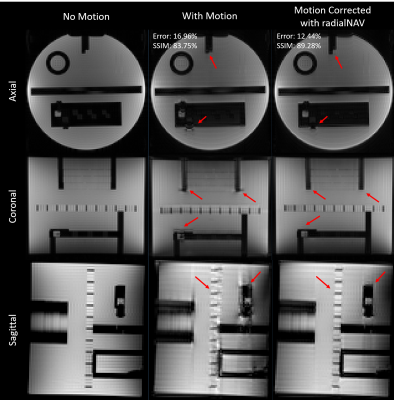
The estimated translation from the motion corrupted dataset is shown in Figure 2, which clearly shows three movements during the scan. In the motion corrupted image, there are clear reductions of spatial information, in particular at the edges (e.g. indicated with red arrows). The structural similarity index (SSIM) between the motion corrupted 3D turbo-FLASH images and the ground truth (no-motion dataset) increased from 83.75%, to 89.28% after motion estimation and correction using radNAV, while the least square error reduced from 16.96% to 12.44%. Fig. 3 highlights motion artifacts and their alleviations after correction (red arrows).

Discussion and Conclusion

This study proposes radNAV and presents its feasibility for motion correction on a phantom. Comparing to other traditional navigators [3-5], radNAV is faster and only occupies < 2ms in each TR for preparation and acquisition. On the other hand, radNAV does not require non-Cartesian gradient or extrapolation of sensitivity maps, making it possible for quick implementation on most sequences. Furthermore, reconstructing and registering low resolution images in self-navigated radial imaging [7-8] is not required. With the implementation of 3D golden angle order [11], a sliding-window approach could be implemented to further increase the temporal resolution (Figure 1C). While it is still possible to estimate translation only with three spokes along X, Y and Z directions (similar as [10]), the multi-spoke frame in radNAV transforms the estimation of translation into an overdetermined problem which gives a higher accuracy, and enables rotation estimation. This, as well as in vivo measurements, are the next steps in our ongoing work.

Acknowledgements

KU received funding from IBS (#IBS-R015-D1). The authors appreciate the support from Dr. Morgan Barense, Dr. Ali Golestani and Ms. Priya Abraham from Toronto Neuroimaging Facility (ToNI), Department of Psychology, University of Toronto.