INTRODUCTION

Multi-echo gradient-echo (mGRE) has been used for many applications including field mapping, susceptibility weighted imaging, myelin water imaging, etc. Subject motion during mGRE data acquisition can cause incorrect allocation values of k-space signal which degrade image quality such as blurring and ghosting artifacts.¹ In previous studies, several retrospective motion correction methods were suggested using navigator echo² or optimizing with data consistency^3,4. However, severe rigid body motion compensation is limited using only the navigator echo.⁵ In addition, since the data consistency-based method has an unstable convergence for calculated problems, this leads to incomplete corrections in the k-space.^3,4

In this work, we propose motion correction framework for mGRE by incorporating navigator echo⁶ and low-rank based reconstruction method.⁷ Motion-corrupted phase encoding lines were detected using navigator echoes which were then reconstructed by eliminating the detected outliers. Additionally, deep learning was adopted to remove residual artifacts.

METHODS

[data acquisition]
mGRE data were acquired from healthy in-vivo with following scan parameters:
3T MRI (Magnetom Tim Trio; Siemens Medical Solution, Erlangen, Germany), scan time = 9:13 min, TR = 46ms, first TE = 1.7ms, echo spacing = 1.1ms, last TE = 34.7ms, (31 echoes with the 31^th echo corresponding to navigator echo), matrix size=128x128x72, resolution = 2x2x2mm³

[Motion correction framework]
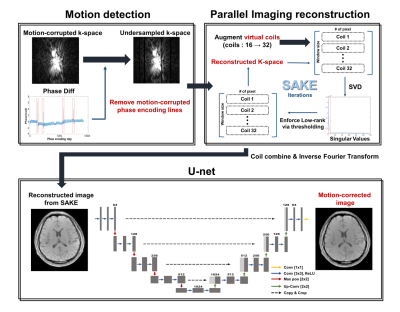
The overall motion correction process is shown in Figure 1. We detected the parts of occurring sudden rigid motion via phase difference from navigator echoes, and eliminated the corresponding k-space lines. In order to compute the reconstruction process from the number of increased coil sensitivity information, spatial encoding of undersampled k-space was expended by using the virtual coil method.⁸ Since conventional parallel imaging techniques, which preserve the auto-calibration signal (ACS) lines, cannot compensate the motion that occurred in the ACS lines, we applied Simultaneous Auto-calibrating and K-space Estimation (SAKE)⁶ reconstruction which is robust against corrupted ACS lines. Finally, reconstructed images which were combined using complex weighted sum were applied to a neural network for removing residual motion artifacts.

[Detecting rigid motion artifact using Navigator echoes]
To calculate phase difference of navigator echoes, images projected on the readout encoding direction was generated by applying Inverse Fourier Transform to the navigator echo signal along this direction. Then phase difference between N^th and the center spatial encoding data point was calculated. The phase difference is shown in Fig. 1, and we can monitor that value of phase difference increased rapidly when rigid motion occurred so that we eliminated the corresponding k-space lines.

[Deep learning process]
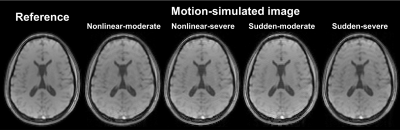
We used U-net⁹ architectures for each 30 echoes (except for navigator echo) to remove residual motion artifacts as shown in Fig. 1. The network was trained with simulated motion-corrupted images as input and motion-free images as label. To simulate rigid motion, k-space lines were phase shifted and rotated in image domain according to Fourier theorem. Training was performed on 5 healthy in-vivo with 4 different motion scenarios per person as shown in Figure 2, and testing was performed on 1 healthy in-vivo (the number of training dataset (for each echo) = 1440).

[Evaluation]
The evaluation proceeded in two ways. First, motion simulation was performed on reference image for quantitative evaluation. Motion scenario used in simulation is shown in Figure 3-a, and k-space lines corresponding to where rigid motion occurred were removed. The SSIM, RMSE values of SAKE, Deep Learning, and proposed method were compared. Second, real motion-corrupted images were acquired by subject motion during scan.

RESULTS

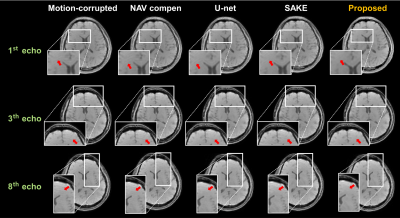
In the motion simulation study, the RMSE and SSIM values were calculated for each method (SAKE, U-net, and proposed methods) (Figure 3-c). The proposed method could achieve the lowest RMSE as well as highest SSIM values. Moreover, in terms of visually observation, the result images show that the proposed method effectively compensated the residual motion artifacts for the simulated motion data as well as the real motion-corrupted data, compared to other methods (marked by red arrows). Figure 4 shows motion compensated mGRE images for each echo.

Discussion and Conclusion

We proposed rigid motion correction method using navigator detection and parallel imaging reconstruction with deep learning. There is a limitation to correct rigid motion from subtracting phase differences or only with the deep neural network trained with motion simulated data because of subject motion’s high degree of freedom. On the other hand, the proposed method shows lower RMSE, higher SSIM, and high similarity compared with reference image when testing simulated motions. In addition, it also outperformed other methods in compensating real motion-corrupted images in terms of visually observation. The proposed method not only showed the potentials as a motion-correction method, but also it may expand to mGRE applications as the future work.

Acknowledgements

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (NRF-2019R1A2C1090635)