1358

Prospective motion assessment within multi-shot imaging using coil mixing of the data consistency error and deep learning

Julian Hossbach^1,2,3, Daniel Nicolas Splitthoff³, Bryan Clifford⁴, Daniel Polak³, Stephan F. Cauley⁵, and Andreas Maier¹
¹Friedrich-Alexander-University Erlangen-Nuremberg, Erlangen, Germany, ²Erlangen Graduate School in Advanced Optical Technologies, Erlangen, Germany, ³Siemens Healthcare GmbH, Erlangen, Germany, ⁴Siemens Medical Solutions, Boston, MA, United States, ⁵Department of Radiology, Athinoula A. Martinos Center for Biomedical Imaging, Boston, MA, United States

Synopsis

In this work we investigate the effect of motion on the data consistency error coil-mixing matrix, obtained by singular value decomposition. More specifically, a Neural Network is trained to translate motion induced deviations of this coil-mixing matrix relative to a reference acquisition into a motion score. This score can be used for the prospective detection of the most corrupted echo trains for removal or triggering a replacement by reacquisition. We show that a selective removal/replacement using the prospective motion score increases the image quality.

Introduction

Motion correction in MRI benefits from the synergy of prospective and retrospective approaches¹. Therefore, gathering insights on the patient’s movements during the acquisition can reduce the prevalence of residual artifacts for retrospective methods². Apart from the prospective correction, knowledge on the motion severity can help physicians to react or it can benefit a retrospective artifact reduction³. In contrast to navigator-^4,5 or camera-based approaches^6,7, our proposed method does not require additional hardware or acquisition disruptions. Instead, we use a scout scan as motion-free reference, which does not interfere with the actual acquisition, to score the motion per echo train (ET).

Theory

It is common practice to use singular value decomposition (SVD)-based techniques to retrospectively compress the raw data $$$k\in\mathbb{C}^{N\times C}$$$ by reducing the number of coils $$$C$$$ and thereby decreasing computational burden of image reconstruction⁸. The SVD creates a set of orthonormal virtual coils sorted by the amount of signal energy contained in each data channel. To determine this linear combination of the coils $$$V_{Ortho}\in\mathbb{C}^{C\times C}$$$, a scout scan $$$k_{Ref}$$$ can be used:
$$k_{Ref} = USV_{Ortho}^H$$
In the presence of motion, the orthonormal base $$$V_{Ortho}$$$ of $$$k_{Ref}$$$ fails to span the new image space efficiently^9,10 as motion results in a redistribution of the signal energy between the channels.
If $$$k_{Ref}$$$ forms a motion-free subset of the motion affected k-space $$$k_{Mot}$$$, the data consistency coil mixing error matrix (CMEM) $$$V_{Err,s}$$$ can be calculated for any subset s, if $$$s\subset k_{Ref} \wedge s \subset k_{Mot}$$$:
$$k_{Ref,s}-k_{Mot,s}=USV^H_{Err,s}$$

Apart from the motion intensity, the CMEM is affected by the object covered by the subset (k-space position, content) and the sensitivity maps.

Method

The goal is to train a Neural Network (NN) (Fig. 3 left), which prospectively scores the motion of k-space subsets, for which the motion is almost stationary, based on the CMEM. This CMEM is calculated using a scout, simulated by a $$$64\times 64$$$ center patch of the motion-free k-space and the k-space after a motion simulation. First, the data is orthogonalized by:
$$\hat{k}=k*V_{Ortho}$$
This reduces the influence of the differences in the sensitivity maps across acquisitions/slices, using $$$V_{Ortho}$$$ from the whole scout. The resulting virtual coils are sorted by their object coverage (Fig. 1) and are used in the further processing (Fig. 2). For no motion, e.g. $$$\hat{k}_{Ref,s}=\hat{k}_{Mot,s}$$$, $$$V_{Err}$$$ is here defined as the identity matrix, in presence of motion off-diagonal values emerge.
The subsets consist of one multicoil ET of $$$\hat{k}_{Ref}$$$ and $$$\hat{k}_{Mot}$$$. For the training, the T2 weighted Turbo Spin Echo (TSE) k-space ($$$256\times 256\times 16$$$) was divided into 8 equidistant ETs, i.e. each ET samples 8 lines in the region of $$$\hat{k}_{Ref}$$$, simulating a homogeneous acquisition. Additional information like the data consistency error of the current ET, the object size relative to the image matrix size and the relative energy of the current ET to the scout was calculated and also provided to the network to account for the differences in the depicted object.
The predicted motion score (MS) is given by the mean Euclidean distance of a virtual k-space sample $$$P=(\sqrt{(d/2)^2}-l^2,l)$$$ moved by the simulated motion $$$M_{\theta}$$$ for each line $$$l$$$ in the current ET ($$$d=1/2*FOV_{Ref}=64 $$$ is number of lines in the scout):
$$MS=\|P-M_{\theta}P\|_2$$

A visualization of the MS is given in Fig. 3 on the right. The MS is independent of the rest of the sampling trajectory, thus it can be estimated prospectively.
The NN receives the complex valued CMEM as individual channels as well as the additional information. The training data was simulated from noise augmented slices from one subject acquired in 5 different head orientations, out of which 2 were used for validation. During training the L2 norm to the ground truth MS is minimized.

Experiments

The experiments investigate whether the NN provide beneficial information for removal or reacquisition of the $$$N$$$ most motion corrupted ET in an iterative reconstruction. For simulating the reacquisition of these ETs, the corresponding ETs are selected from the motion-free k-space.

Results

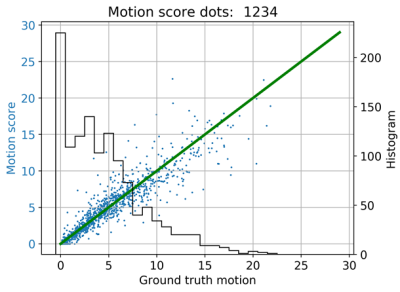
In Fig. 4 the regression plot and the histogramm of the ground truth MS is depicted. Fig. 5 shows reconstructions by removing or replacing the most corrupt ETs according to the network. The simulated motion is depicted below, and the number indicates the ranking for the ET based on the NN's output. Here, the network estimates a good ranking of the motion severity, only ET 4 and 5 are inverted.

Discussion

In the simulated setting our results show that prospective detection of motion based on deviations of the coil-mixing matrix is possible and can be used to trigger the reacquisition of selected ETs. Apart from the requirement for the ET acquisition to overlap with the scout scan, no modifications of the sequence, such as navigators, is needed. Future work might include the prediction whether the final motion state allows a reacquisition of a specific ET, which fits the other orientations of the remaining ETs. In case of a different final position the removal of a limited number of ETs can lead to an improved image quality in the iterative reconstruction compared to a reacquisition. Furthermore, a larger variety of coil settings and subjects needs to be investigated.

Acknowledgements

No acknowledgement found.

References

¹Zaitsev M., Maclaren J., Herbst M. Motion artifacts in MRI: A complex problem with many partial solutions. J Magn Reson Imaging 2015; 42(4); 887-901

² Castella R., Arn L., Dupuis E., Callaghan M., Draganski B, Lutti A. Controlling motion artefact levels in MR images by suspending data acquisition during periods of head motion. Magn Reson Med. 2018 Dec; 80(6);2415-2426

³ Oksuz I., Clough J., Ruijsink B. et al Detection and Correction of Cardiac MR Motion Artefacts during Reconstruction from K-space. Proc. MICCAI 2019; 695-703

⁴ Sachs T., Meyer C., Hu B., Kohli, J., Nishimura D., and Macovski A. Real‐time motion detection in spiral MRI using navigators. Magn. Reson. Med. 1994 32(5); 639-645.

⁵ Tisdall M., Hess A., Reuter M., Meintjes E., Fischl B., van der Kouwe A., Volumetric navigators for prospective motion correction and selective reacquisition in neuroanatomical MRI. Magn. Reson. Med. 2012 68(2); 389-399

⁶ Qin, L., van Gelderen, P., Derbyshire, J., Jin, F., Lee, J., de Zwart, J., Tao, Y. and Duyn, J. Prospective head‐movement correction for high‐resolution MRI using an in‐bore optical tracking system. Magn. Reson. Med. 2009 Oct; 62(4); 924-934

⁷ Dold C., Zaitsev M., Speck O., Firle E., Hennig J., Sakas G. Advantages and Limitations of Prospective Head Motion Compensation for MRI Using an Optical Motion Tracking Device, Academic Radiology 2006, 13(9); 1093-1103

⁸ Zhang T., Pauly J., Vasanawala S., Lustig M. Coil Compression for Accelerated Imaging with Cartesian Sampling. Magn. Reson. Med. 2013; 69(2); 571–582

⁹ Duerk J., Wu D., Chung Y., Liang Z., Lewin J. A simulation study to assess SVD encoding for interventional MRI: effect of object rotation and needle insertion. J Magn Reson Imaging. 1996; 6(6); 957-960

¹⁰ Kurucay K., Schmalbrock P. Analysis of SVD encoded imaging in the presence of inplane motion. ISMRM 1995; 755.

Figures

Fig. 1: Example sensitivity maps before and after mixing with V_Ortho.

Fig. 2: Processing pipeline for prospective motion scoring.

Fig. 3: Structure of the Neural network with respective output sizes (left) and the visualization of the MS (right).

Fig. 4: Plot of the ground truth MS vs. network output. The green line indicates the perfect regression and the histogram is calculated over the ground truth MS.

Fig. 5: Reconstruction of the motion corrupted k-space by removing or replacing the highest ranked ET by the NN (RMSE: red; SSIM yellow). The curve in the plot below shows the ground truth motion; the numbers represent the ranking of the motion severity obtained by the NN. For simplicity only rotation is simulated in this example.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1358