Introduction

Patient motion continues to be a major problem in MRI, although tremendous advances have been made using post-processing or prospective correction strategies^1,2, and more recently deep learning (DL)^3-5. While encouraging, these studies represent a direct application of existing network architectures to relatively minor motion artifacts, leaving much room for further optimizations. We propose a two-stage and multiple-loss based MRI motion correction network (MC-Net). In the first stage, MC-Net was trained with an L1 loss function to drive the network output as close as possible to the reference (motion free images). The second stage was then trained to minimize the L1 and Total Variation (TV) of the residual image (output-reference). The goal was to suppress the overall motion-induced artifacts which often affect tissue boundaries the most.

Methods

Simulation of Motion Corrupted Images
78 motion trajectories of 128 points each were synthesized from in-vivo head movements measured with PACE fMRI¹ (all <2mm/2°, each with 6DOF), and multiplied by eight. Trajectories were offset such that the k-space center remained in the origin point.
The source images were 3D MP-RAGE scans of 52 subjects (1mm isotropic; 256×256×160) without motion artifacts. For each of the 78 trajectories, the motion-corrupted k-space trajectory was calculated² (resolution 128×128×128) and sampled with non-uniform FFT (NuFFT)⁶. Ten sagittal slices were extracted from the resulting motion-corrupted 3D datasets (5mm increments; total 780 slices per subject). Two simulations were performed: in-plane rotations only, and in-plane translations and rotations. After removing boundary slices, the final dataset contained 41,750 slices (128×128). This was divided into a training set (35 subjects/28,800 slices), validation set (5 subjects/4,320 slices), and test set (12 subjects/8,630 slices).
MC-Net
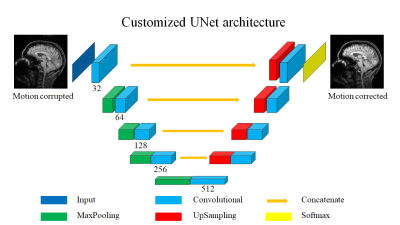
Fig. 1 shows the architecture of MC-Net, which was derived from UNet⁷. The major novelty is the hybrid loss function L, which combines a L1-loss and Total Variation loss (TV)⁸:
$$L = alpha×L1 + beta×TV$$ (1)
$$𝑇𝑉= \sum_{i,j}((𝐼(𝑖+1,𝑗)−𝐼(𝑖,𝑗))^2+(𝐼(𝑖,𝑗+1)−𝐼(𝑖,𝑗))^2)^{1.25}$$ (2)
where I is a corrupted image; i, j are row/column indices.
The second novelty is the two-stage training strategy. Stage 1 uses L1-loss only [set (alpha, beta) = (1, 0)] to suppress the overall motion-induced artifact. The pre-trained stage 1 model is then fine-tuned in stage 2 by turning on the TV-loss component [(alpha, beta) = (1, 1)]; this penalizes boundary artifacts in addition to overall artifacts. For comparison with the two-stage MC-Net (abbreviated “L1+TV-ft”), single-stage models trained with the L1-loss⁵ and L1 + TV loss-only were also implemented (“L1” and “L1 + TV” models). All models were trained in 100 epochs, using the Adam optimization method⁹. The structural similarity index measure (SSIM) with the “clean” image as reference¹⁰ was used to quantify the performance of each method. The quality of images was also assessed visually by 2 experienced readers.
Radiology Scores
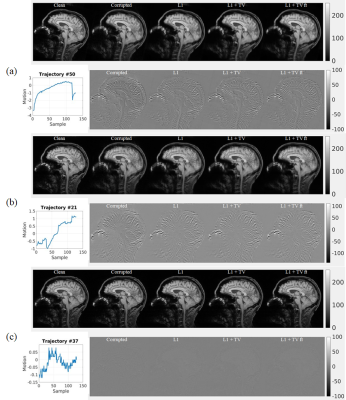
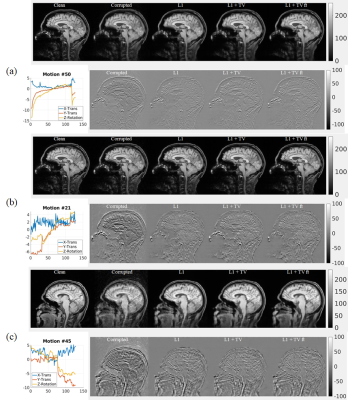
Mid-sagittal slice of 5 selected patients from 3 groups of images: reference images, motion corrupted images and MC-net prediction were reviewed by two experienced readers. Five distinct motion trajectories with different standard deviation of z-rotation (in the experiment of z-rotation only) or summed standard deviations of z-rotation (°) and x-translation (mm) and y-translation(mm) were used in these chosen images.

Results

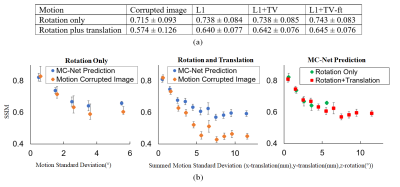
Representative results of L1, L1+TV, and L1+TV-ft are shown in Fig.2 (rotation only artifact) and Fig.3 (rotations plus translations). All DL methods improved image quality, but the MC-Net was slightly more effective than the other methods.
Fig. 4a compares the SSIM (mean ± std) for various models. The proposed 2-stage L1+TV-ft method improved the image quality slightly better than conventional approaches, both for the rotation only and rotation plus translation models. Fig.4b shows that the SSIM decreases with the motion magnitude (standard deviation across 128 time points), from >0.8 for small motions (sub-mm/degree) to <0.5 for severe movements. The proposed 2-step L1+TV-ft approach improved image quality for motion magnitudes >1, but was especially effective for large rotation plus translation movements (Fig.4b, center).
Fig. 5 shows readers’ visual assessment of reference images, motion corrupted images, and the MC-Net prediction against the motion magnitude. The scores were on a scale from 0 to 5 (0 = no diagnostic value; 5 = no artifacts). The average scores from these two experienced readers demonstrate the improvement in image quality due to the proposed MC-Net (red circles versus blue X). Notably, improvements were most pronounced when both rotations and translations are present and motion artifacts are most severe (Fig.5, right).

Discussion

The MC-Net can correct motion artifacts in brain scans, in agreement with previous work^3-5. We based our experiments on a customized UNet architecture⁷ because it is widely used in medical image analysis. Also, the UNet architecture is complex enough to perform the motion correction task, but also simple enough to demonstrate the merits of the proposed hybrid loss. Implementation using the open-source framework Keras¹¹ with GPU acceleration might allow real-time motion correction. The proposed novel hybrid loss and two-stage training was slightly better in improving the final image quality than existing approaches, and was especially beneficial for correcting large rotational and translational motion artifacts.

Conclusion

We propose a simulation framework and MC-Net for motion correction in MRI. Since the method is data-driven and independent of data acquisition or reconstruction, it may be suitable for routine clinical practice.

Acknowledgements

This work was supported by NIH grant 1R01 DA021146 (BRP) and NIH/NIA R01AG060054.