1349
A General Framework for Automated and Accurate b-Matrix Calculation for dMRI Pulse Sequences1Department of Biomedical Engineering, Center for Brain Imaging Science and Technology, Zhejiang University, Hangzhou, China, 2MR Collaborations, Siemens Healthcare Ltd., Shanghai, China, 3SHS DI MR R&D SZN LP, Siemens Shenzhen Magnetic Resonance Ltd., Shenzhen, China, 4Department of Imaging Sciences, University of Rochester, Rochester, NY, United States
Synopsis
Since both imaging and diffusion gradient pulses could lead to significant diffusion-related signal attenuation, one must account for the effect of all imaging and diffusion gradient pulses to achieve an accurate estimation of diffusion metrics and tensors. Based on a generalized definition of b matrix, a general framework for an automated and accurate b-matrix calculation was proposed in this study. Its correctness was verified in SE-diffusion sequence, and the importance of accurate inclusion of all gradient pulses was shown in both SE- and SPEN-diffusion sequence. The proposed method is suitable for accurate evaluation of diffusion effects in various sequences.
Introduction
With gradients pulses inserted into an MRI imaging sequence, so-called diffusion-weighted images are obtained to depict the random movement of water molecules, providing valuable information regarding the microstructure of tissues1. Usually, only diffusion gradients were considered to account for the diffusion-related attenuation effects. However, the diffusion effect from imaging gradients was not always ignorable. In such cases, all gradient pulses should be taken into consideration for accurate b-factor or b-matrix calculations.Commonly, b-matrix can be obtained using experimental evaluation, numerical calculation, or analytic solution. An experimental method needs a dedicated phantom to calibrate the diffusion coefficient, while the numerical and analytical calculations become tricky (sometimes unsolvable) when dealing with complicated imaging pulse sequences. Calibrations with all the methods may also depend on specific imaging parameters. In this study, a general framework was proposed for an automated and accurate calculation of b matrix, which considers the effects of all gradient pulses. Two examples were provided to indicate where such accurate b-matrix calculation is necessary.
Methods
A generalized definition of b matrixGiven the gradient pulse $$$\textbf{G}(t)=\left[G_{x}(t), G_{y}(t), G_{z}(t)\right]$$$ , a generalized analytical expression of the b matrix can be expressed as follows2,
$$\textbf{b}=\gamma^{2}\int_{0}^{TE} \left[\textbf{F}(t)-2\xi(t)\textbf{f} \right]^{T} \left[\textbf{F}(t)-2\xi(t)\textbf{f} \right]dt \hspace{1cm}[1]$$
Here $$$\textbf{F}(t)=\int_{0}^{t} \textbf{G}(t^{'})dt^{'}$$$ is a piecewise function summarizing the action of all gradients of each axis up to a particular time t, and TE is the effective echo time. For a 2D spin echo (SE)2 or SE-EPI sequence3, $$$f=F(\frac{1}{2}TE)$$$ was recorded to account for the antiphase effect of the180° RF pulse. Besides, $$$\xi(t)=0$$$ when $$$0 \leq t \leq \frac{1}{2}TE$$$, and $$$\xi(t)=1$$$ when $$$\frac{1}{2}TE \leq t \leq TE$$$ . Based on Eq. [1] and vector multiplication principle, the element of the b matrix containing contributions from interactions between gradient pulses applied along the same or orthogonal directions could be obtained,
$$b_{ij}=\gamma^{2}\int_{0}^{TE} \left[F_{i}(t)-2\xi(t)F_{i}\left(\frac{1}{2}TE\right)\right] \left[F_{j}(t)-2\xi(t)F_{j}\left(\frac{1}{2}TE\right)\right]dt \hspace{1cm}[2]$$
The indexes i and j indicate the coordinate directions in which the gradient pulses are applied (i.e. the read, phase, or slice direction).
A general framework for an automated and accurate b-matrix calculation
Based on the acquisition protocols, the sequence timing (as in Figure 1a) was simulated according to the specific scanner platform. Taking the effect of all gradient pulses into account, a general framework was proposed in this study to achieve an automated and accurate b-matrix calculation. A detailed schematic of the processing pipeline was shown in Figure 1b.
Results
Here two dMRI sequences were listed as examples indicating the necessity of accurate calculation in the cases where imaging gradients have a significant diffusion-related attenuation effect.Case 1: spin-echo (SE) imaging sequence
As indicated in a previous study2, attention should be paid to the diffusion-related signal attenuation caused by the imaging gradients of SE sequence when there is a pair of crusher gradients or the read-dephase gradient is not rephased immediately (see Figure 2). To confirm the significant impact of imaging gradients as well as the validity of our method, the diagonal elements of the b matrix were calculated using our proposed framework and compared with those analytical expressions derived in ref. [2].
Based on the simulation protocol in ref. [2], Table 1 showed that the numerical b-matrix calculated from our method is consistent with the analytical values. Moreover, the read-dephase gradient had a significant effect on the bread when there is no Gcrusher and no Gdiff applied. Furthermore, with the increasing amplitude, crusher gradients had an increased effect on the diagonal elements of the b matrix even when Gdiff = 0 mT/m.
Case 2: spatial-temporal encoding (SPEN) sequence
SPEN sequence4 has received wide attention due to its significantly reduced geometric and intensity distortions. For this sequence (Figure 3a), the interaction between the excitation and diffusion gradient pulses produces non-negligible “cross-terms”, and the unique excitation instant for each position leads to spatial-dependent b-values along the SPEN-axis5. In this study, the diffusion gradients were applied only along SPEN-axis to illustrate the effect of excitation gradient on the element $$$b_{yy}$$$ calculation. Given the excitation gradient with a positive polarity and chirp pulse with the symmetric linear decreasing frequency, the negative end of the sample along SPEN axis ($$$y=-L_{y}/2$$$) was excited last but refocused first, resulting in a minimal effect of imaging gradients.
Figure 3 illustrated the SPEN sequence and its $$$b_{yy}$$$ values along SPEN axis. It showed that the values at $$$y=-L_{y}/2$$$ were basically unaffected if the imaging gradients were ignored. By contrast, the $$$b_{yy}$$$ values at $$$y=L_{y}/2$$$ had a large deviation from the accurate value when the effects of imaging gradients were not considered.
Discussion and Conclusion
In this study, a general framework was proposed to calculate b matrix automatically and accurately based on the sequence timing. The accurate calculation proved to be necessary in the cases where the imaging gradients have a significant diffusion-related attenuation effect. In the future, the importance of the accurate b-matrix calculation can also be explored in the cases where small disturbances of b value significantly affect the results, such as in the application of the intravoxel incoherent motion (IVIM) model6, or in cases where effective diffusion weighting may be altered by significant susceptibility changes, such as injection of contrast agent7,8.Acknowledgements
No acknowledgement found.References
1. Le Bihan D., 2011. Chapter 5: Magnetic resonance diffusion imaging: Introduction and concepts. In: Jones, D.K. (Ed.), Diffusion MRI: Theory, Methods, and Applications. Oxford University Press, Oxford, United Kingdom, pp. 57–78.
2. Mattiello J, Basser PJ, Le Bihan D. Analytical expressions for the b matrix in NMR diffusion imaging and Spectroscopy. J. Magn. Reson., 1994; 108: 131– 141.
3. Mattiello J, Basser PJ, Le Bihan D. The b‐matrix in diffusion tensor echo‐planar imaging. Magn. Reson. Med., 1997; 37: 292– 300.
4. Chen Y, Li J, Qu X, et al. Partial Fourier transform reconstruction for single-shot MRI with linear frequency-swept excitation. Magn. Reson. Med., 2013, 69(5):1326-1336.
5. Solomon E, Shemesh N, Frydman L. Diffusion weighted MRI by spatiotemporal encoding: Analytical description and in vivo validations. J. Magn. Reson., 2013, 232:76-86.
6. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology, 1988; 168:497-505.
7. Zhong JH; Kennan RP; Gore JC. Effects of Susceptibility Variations on NMR Measurements of Diffusion. J. Magn. Reson., 1991; 95: 267.
8. Does MD; Zhong JH; Gore JC. In-Vivo Measurement of ADC Change Due to Intravascular Susceptibility Variation. Magn. Reson. Med., 1998; 41: 236.
Figures
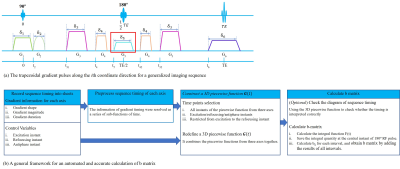
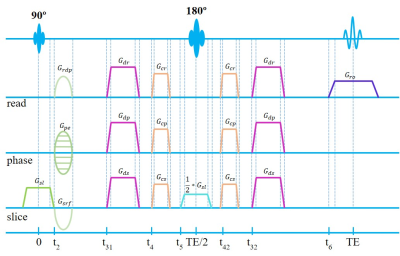
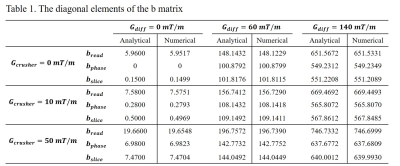
Table 1. The diagonal elements of the b matrix calculated based on the simulation protocol of ref. [2]. The results calculated from analytical expressions (Eqs. [17-19] of ref. [2]) were compared with the values calculated using the proposed automated framework.
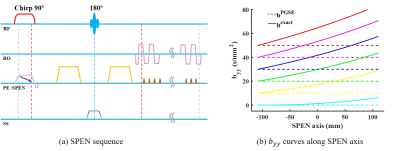
Figure 3. The SPEN sequence and its byy curves along SPEN axis. The byy curves calculated from all gradient pulses (byyexact, solid lines) were compared with those solely considering the contributions from diffusion gradients (byyPGSE, dashed lines).