Introduction

Although multi-shot EPI with multiplexed sensitivity encoding (MUSE) can improve the spatial resolution and geometric accuracy for diffusion MRI¹, MUSE is less feasible for the data acquisition of high angular resolution diffusion imaging (HARDI) due to increased scan time. Various acceleration methods based on undersampling in k_y-d space have been proposed to achieve HARDI with improved scan efficiency and reduced distortion^2-4. However, the in-plane acceleration factor (R_ky) is limited by the number of coils because the data reconstruction still relies on parallel imaging^{5, 6}. Previous studies showed that the dimensionality reduction approaches can transform the ill-conditioned reconstruction problem (e.g., R_ky > number of coils) into overdetermined problem with predetermined features, such as k-t PCA⁷. In light of this, we proposed a k-d singular value decomposition (SVD) reconstruction method to achieve over 8-fold in-plane acceleration for multi-shot HARDI even using an 8-channel phase-array head coil.

Methods

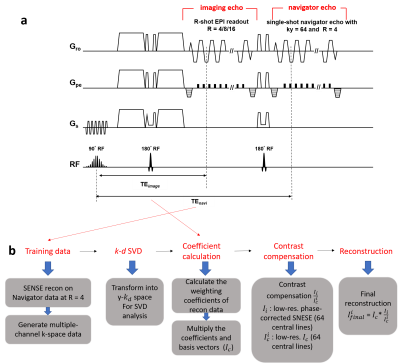
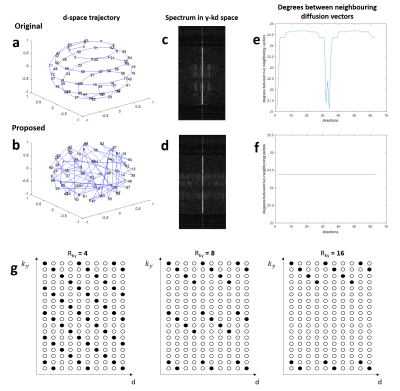
Design of pulse sequence
Because SVD requires training data to identify the basis vectors, the 2D navigator echo is implemented into an interleaved diffusion-weighted EPI (DW-EPI) sequence to acquire the training data for SVD (Fig.1a). For the navigator echo, the number of k_x sampling remains the same as imaging echo, but only 64 central k_y lines is acquired with R_ky=4. A previously reported smooth ordering of diffusion directions is used to acquire the HARDI data for reduced spectrum overlaps in y-k_d space³ (Fig.2a).
Data reconstruction
Each spectrum in y-k_d space can be approximated by a linear combination of a set of predetermined basis vectors because of its sparsity. To increase the incoherence, the acquired data are reordered along d-space, with an ascending order of g^TDg(where g is the gradient vector and D is diffusion tensor transformation matrix) as shown in Fig.2b. After data reordering, first, the 4-fold undersampled 2D navigator data of each diffusion direction is reconstructed using conventional SENSE⁵, and then used to generate multi-channel data by multiplying with coil sensitivity profiles. Second, for the k_y-d plane at each x location, the data is Fourier transformed to y-k_d space, and SVD is performed on it to extract the basis vectors and the corresponding weighting coefficients ($$$w_{train,x}$$$). Third, the weighting coefficients for the reconstruction data ($$$w_{x}$$$) are calculated using least square method as shown in Eq.1, with the signal covariance matrix ($$$M_x^2$$$) pre-derived from $$$w_{train,x}$$$ using Eq.2⁷.
$$$w_{x}=M_x^2E^{H}(EM_x^2E^{H}+\lambda I)^{+}P_{alias,x}$$$ (1)
where $$$E$$$ is encoding matrix that contains basis vectors and $$$P_{alias,x}$$$ is the aliasing pixel in the spatial position x.
$$$M_x^2=diag(|w_{train,x}|^{2})$$$ (2)
Fourth, the reconstructed data at y-k_d space at each x location is recovered by multiplying the $$$w_{x}$$$ with the basis vectors, and then transformed to y-d space. Finally, the contrast compensation is performed for reconstructed images using the scaling factor calculated from the division between the reconstructed images and the phase-corrected training data⁸. The complete flowchart is shown in Fig.1b.
Hybrid simulation
Data acquisition: HARDI data were acquired from one healthy subject using an 8-channel head coil on a 1.5T GE scanner (Explorer, GE Healthcare) with following parameters: matrix size=128x128, number of shots=4, b=800s/mm² with 64 diffusion directions, slice thickness=5mm, and TR/TE = 4350/72.4ms. The Nyquist ghost-corrected 4-shot HARDI data were firstly reconstructed using MUSE¹, and considered as gold-standard images without any acceleration in data acquisition.
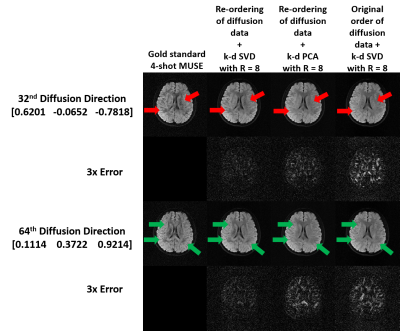
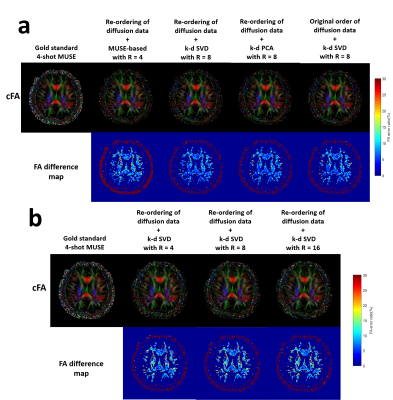
Simulation 1: Three strategies of data reconstruction using dimensionality reduction approaches and proposed pipeline were evaluated from the simulated data with R_ky=8 (Fig.2g), including i) k-d PCA with re-ordering of diffusion data, and k-d SVD ii) with and iii) without re-ordering of diffusion data.
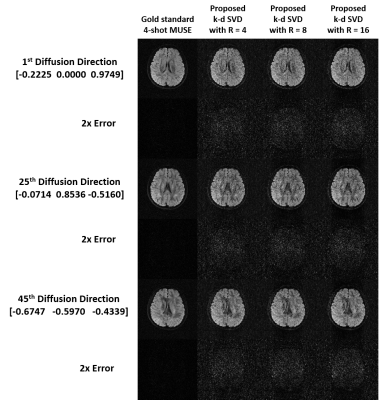
Simulation 2: The proposed k-d SVD reconstruction with re-ordering of diffusion data was evaluated for the simulated data with three different in-plane acceleration factors (Fig.2g; R_ky=4, 8, and 16). Training data were generated from the SENSE-produced images of originally acquired k_y segment (from the 4-shot data) with 64 central k_y lines and R_ky=4 (i.e., simulation of navigator echo). The 4-shot fully-sampled data was reconstructed using MUSE¹ for comparison.

Results

Fig.3 shows the comparison of diffusion images produced from three strategies of data reconstruction using dimensionality reduction approaches and proposed pipeline. Fig.4 shows the comparison of the reconstructed images at different acceleration factors using proposed k-d SVD. Figure 5 shows the comparison of cFA maps produced from the data reconstructed with different methods and acceleration factors.

Discussion and conclusion

Our hybrid simulation demonstrates that the reconstruction performance of the proposed k-d SVD method for different in-plane acceleration factors (R_ky=4, 8 and 16) is comparable with the MUSE-based method³ with R_ky=4. From our evaluation, the performance of k-d SVD is affected by the order of diffusion data that requires an ascending order of g^TDg for optimizing the performance (i.e., less error to gold standard). As expected, k-d SVD is better than k-d PCA because k-d SVD can preserve more features of direction-specific contrast. In addition, the reconstruction performance of k-d SVD may less rely on the available number of coils that makes high acceleration factor feasible, even with limited number of coils (i.e., R_ky > number of coils). In conclusion, the proposed k-d SVD method can achieve high acceleration for multi-shot HARDI acquisition, without sacrificing the data quality and relying on the number of coils.

Acknowledgements

The work was in part supported by grants from Hong Kong Research Grant Council (GRFs HKU17121517 and HKU17106820) and Hong Kong Innovation and Technology Commission (ITS/403/18). We thank Tzu-Cheng Chao for useful discussion and the help on data acquisition.