Purpose

The Diffusion-weighted (DW) magnitude is commonly Rician or non-central $\chi$ distributed, with a signal elevation falsely caused by the noise-floor [1,2]. To mitigate the noise-floor issue, phase correction extracts real-valued Gaussian-distributed diffusion MRI data, eliminating biases of white-matter microstructure estimation (WM-MSE), e.g., fractional anisotropy (FA). Conventional phase correction methods resort to employing spatially-adaptive filters for improving perfromance [3,4]. However, even MPPCA [5], renowned as spatial adaptivity, surprisingly introduces severe artifacts [6]. This unexpected observation unveils underlying issues of phase correction, which inspire us to cautiously analyze and reformulate phase correction procedures.In this abstract, we propose a calibrated procedure for phase correction.

Methods

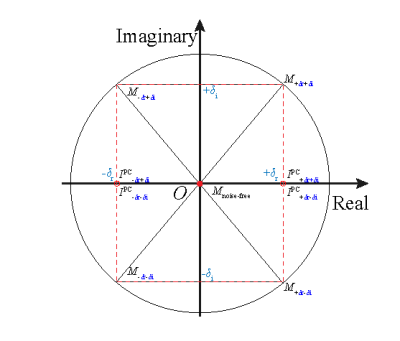
Phase correction complex-rotates actual image contents, $$ I^\text{PC}({x}) = M(x){\rm e}^{j(\varphi({x}) - \varphi_{\text{BG}}({x}))}, $$ Given the magnitude $$$M(x)$$$ and phase $$$\varphi({x})$$$, the phase-corrected result $$$I^\text{PC}({x})$$$ is determined by the background phase $$$\varphi_{\text{BG}}({x})$$$, $$$ \varphi_{\text{BG}}({x}) = \arctan{\frac{f(I_\text{i}({x}))}{f(I_\text{r}({x}))}}, $$$ where $$$x$$$ and $$$f(\cdot)$$$ denote a voxel location and the filtering operator on real $$$I_\text{r}({x})$$$ and imaginary $$$I_\text{i}({x})$$$ parts of DW images, respectively; and $$$I^\text{PC}({x}) = I_\text{r}^{\text{PC}}({x})+j{I}_\text{i}^{\text{PC}}({x})$$$, $$ I_\text{r}^{\text{PC}}({x}) = M({x})\cos({\varphi({x})-\varphi_{\text{BG}}({x})}),\\ I_\text{i}^{\text{PC}}({x}) = M({x})\sin({\varphi({x})-\varphi_{\text{BG}}({x})}). $$ Fig.1 pictorially depicts a noise-free voxel $$$I({x}) = 0 + j0$$$ with $$$M_\text{noise\_free} = 0$$$. When reconstructing $$$M_{-\delta\text{r}-\delta\text{i}}$$$, the noises are typically flipped from negative to positive, and thus result in the noise-floor. By contrast, phase correction results in $$$I^\text{PC}_{-\delta\text{r}-\delta\text{i}} + I^\text{PC}_{+\delta\text{r}+\delta\text{i}} = 0$$$ instead of $$$M_{-\delta\text{r}-\delta\text{i}} = M_{+\delta\text{r}+\delta\text{i}}$$$.

In Fig.1, phase correction procedures misleadingly give $$$I^\text{PC}_{-\delta\text{r} + \delta\text{i}}$$$ and $$$I^\text{PC}_{-\delta\text{r}-\delta\text{i}}$$$ the same result. More specifically,$$$I^\text{PC}_{-\delta\text{r} + \delta\text{i}}$$$ is derived only from positive noise in the imaginary axis and negative noise in the real axis, while $$$I^\text{PC}_{-\delta\text{r}-\delta\text{i}}$$$ is derived from negative noises in both axes. $$$I^\text{PC}_{-\delta\text{r} + \delta\text{i}}$$$ is falsely as smaller as $$$I^\text{PC}_{-\delta\text{r} - \delta\text{i}}$$$, and that is the reason why conventional phase correction falsely introduces dark holes.

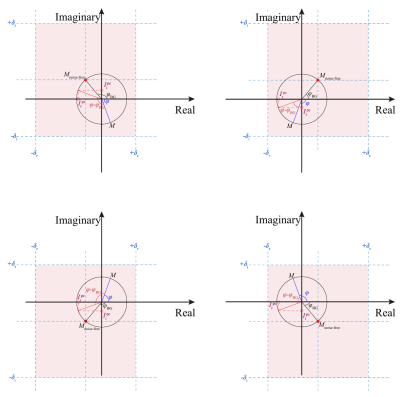
To eliminate the dark holes, we calibrate phase correction procedures, by horizontally flipping $$$I^\text{PC}({x})$$$ with $$$\pi/2 < {\varphi({x})-\varphi_{\text{BG}}({x})} < -3\pi/2$$$ towards the first or the fourth quadrant, in a way analogous to the magnitude reconstruction. Meanwhile, the calibrated phase correction procedures assign negative values to voxels that are most likely to cause the noise-floor; and Fig.2 demonstrates the voxels that correspond to regions of high confidence in inducing noise-floor.

Results

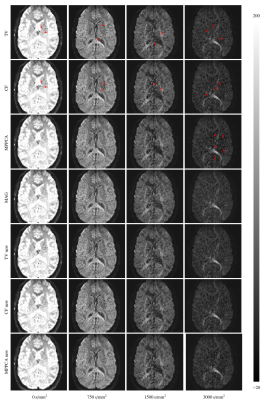
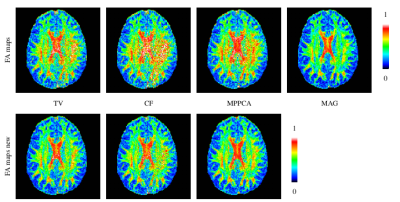
We generated synthetic DW data using Phantom$$$\alpha$$$s [7] with the same gradient vectors of the real data described as follows. We synthesized the background phase according to [2]. With the noise-free DW images, we added spatially varying Gaussian noises to the real and imaginary parts, respectively. The real DW images were acquired using a SIEMENS 3T Magnetom Prisma MR scanner with following protocol, TR =$$$2500 \text{ms}$$$, TE=$$$89 \text{ms}$$$, FoV=$$$210\times 210\,\text{mm}^2$$$, matrix size=$$$140\times140$$$, and $$$b=750,1500,3000\,\text{s/mm}^2$$$ with a total of $$$64$$$ diffusion directions. To demonstrate the improvement, we compared conventional phase correction procedures with the calibrated ones, both of which employed filters with the same parameters, including curvature filtering (CF) [8], total variation (TV) [1], and Marchenko-Pastur PCA (MPPCA) [5].
Fig.3 shows synthetic FA maps derived from TV, CF, and MPPCA, with increased FA values of white-matter compared to magnitude (MAG). Furthermore, it can be seen from error maps that the calibrated phase correction procedures yield the results that are closer to the ground-truth, especially for MPPCA. Fig.4 demonstrates the calibrated phase correction procedures introduce significantly fewer dark holes to the phase-corrected real images, as shown in Fig.5 where the artifacts introduced by conventional phase correction are effectively eliminated.

Conclusion

We calibrated the phase correction procedures to avoid arbitrarily specifying negative values, which should only be derived from the noise-floor. The calibrated procedures fully exploit the use of the advanced filter, e.g, MPPCA, which can be effectively employed to mitigate the noise-floor in DW images without introducing additional artifacts.

Acknowledgements

This work was supported in part by National Natural Science Foundation of China (No. 62073260, 61971350).