Introduction

Diffusion MRI offers a powerful approach to map tissue microstructure. However, it intrinsically suffers from low SNR, especially when spatial resolution or b-value is high. A typical diffusion MRI session produces image sets with same geometries but different diffusion directions and b-values. These diffusion-weighted (DW) images often share strong structural similarities despite their contrast differences. This study proposes a new method for jointly denoising DW images. In brief, similar patches from a DW image set are extracted to form low-rank patch matrices, and low-rank matrix approximation method is then applied to estimate noise-free patch matrices. The proposed method was evaluated with simulated and in vivo brain DW images.

Methods

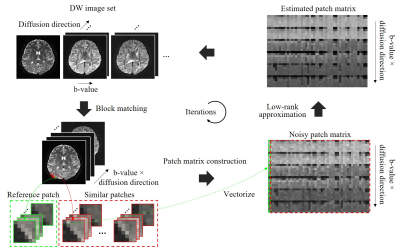
Denoising Method

The proposed joint denoising method consists of following steps (Fig. 1).
1) Block matching: By sliding a 3D window across the entire DW image set, 3D reference patches are extracted. For each reference patch, k similar patches are searched based on Euclidean distance.
2) Patch matrix construction: A noisy patch matrix is constructed by stretching k similar patches to vectors and stacking them into a matrix. The patch matrix is then multiplied by a weighting matrix, which is a diagonal matrix and determined by the noise level of each image.
3) Low-rank approximation: A weighted nuclear norm minimization (WNNM) model^1,2 is applied for estimating noise-free patch matrices. For each noisy patch matrix, estimated patch matrix can be obtained by performing matrix singular value decomposition to the patch matrix, and then singular-value thresholding of the singular matrix.
4) Recovering DW image set from estimated patch matrices.

Evaluation

Simulation Experiment: The simulated brain data was originally created for ISMRM 2015 Tractography challenge³. The dataset contains one b=0 image and 32 DW images with b-value=1000 s/mm². The matrix size is 90×108×90 with 2-mm isotropic resolution. One b=0 image and 6 DW images were extracted to form a ground truth image set to evaluate the proposed denoising method for simple DTI. Rician noise (4% of the maximum intensity) was added to form noisy DW images.

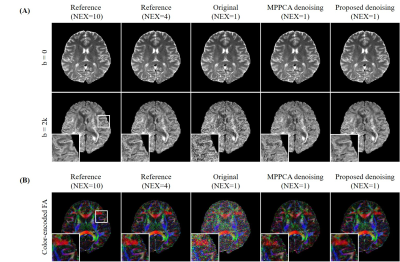
In Vivo Experiment: Two brain datasets were acquired on a 3T Philips scanner using an 8-channel coil by 4-shot interleaved EPI with matrix size=220×220, slice number=10. The imaging parameters for the first dataset were TR/TE=2400/118ms, 6 diffusion directions with b=2000s/mm² and a b=0 image. The scan was repeated 10 times for a high SNR reference. The imaging parameters for the second dataset were TR/TE=2500/123ms, 6 diffusion directions with b=1000/2000/3000 s/mm² and a b=0 image. The scan was repeated 4 times. For both datasets, the DW images of single average were used as noisy image sets for denoising.

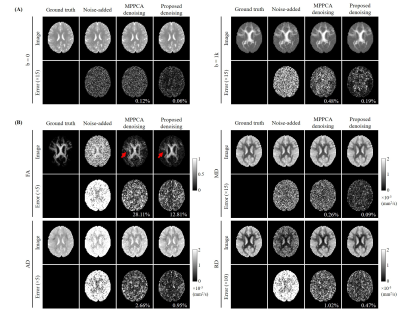
The denoising was also performed through MPPCA^4-6 for comparison. Variance stabilizing transformation (VST)⁷ and inverse VST were performed to the noisy image sets before and after denoising respectively, so that the Rician noise could be treated as noise with unitary variance. For the proposed denoising method, the sliding window size was 4×4 and similar patch number was k=140. FSL DTIFit Toolbox⁸ was used to derive quantitative diffusion maps. In simulation experiment, the error maps were calculated by subtracting denoised images from ground truth images, and normalized root-mean-square errors (NRMSE) were measured.

Results

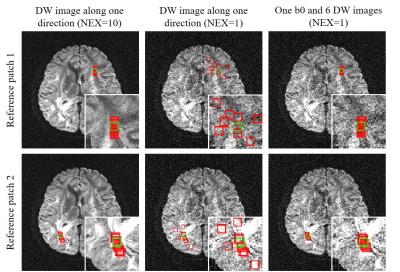
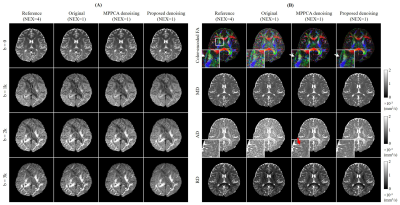
Figs. 2-5 show the denoising performance of our proposed method. Fig. 2 presents denoising results for simulated images. Our method effectively reduced noise in all DW images while preserving structural details, resulting in smaller NRMSEs than MPPCA for denoised images and quantitative diffusion maps. Fig. 3 shows the denoising results for in vivo brain image set containing one b0 image and 6 DW images. When DW images had low SNR, MPPCA became less effective, while the proposed method reduced the noise significantly and achieved image quality and FA map comparable to those using 4 averages. Note that at low SNR, the proposed method still maintained high accuracy in searching similar patches (Fig. 4) by exploiting the structural similarities among DW images. Fig. 5 presents denoising results for in vivo image set containing one b0 image and DW images with 6 directions and 3 b-values. The results again demonstrated that our proposed method was effective in reducing noise, with FA revealing more microstructural details.

Discussion and Conclusions

In conclusion, this study presents a new method for jointly denoising DW images. The proposed method exploits structural similarities of diffusion-weighted images, yielding significant noise reduction in all images and revealing more microstructural details. The superior performance of our proposed method is based on the rationale that similar patches from noisy images can be extracted and used to form a patch matrix, which should be a low-rank matrix and thus can be recovered through low-rank matrix approximation. Further studies can be carried out in three directions. First, the method will be extended to jointly denoise multi-slice DW images. By concatenating multi-slice patch matrices, a low-rank patch tensor can be obtained and high-order singular value decomposition can be performed for the low-rank tensor approximation. Second, the noise level estimation will be optimized in a patch-based way so that the proposed method can be more robust for non-uniformly distributed noise. Third, the proposed method will be evaluated for advanced diffusion MRI techniques, such as tractography, Q-ball imaging and kurtosis imaging.

Acknowledgements

This study was supported by Hong Kong Research Grant Council (R7003-19, C7048-16G, HKU17112120, HKU17103819 and HKU17104020), Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001), and Guangdong Key Technologies for Alzheimer’s Disease Diagnosis and Treatment (2018B030336001).