Introduction

Intravoxel incoherent motion (IVIM)¹has been widely used to separate diffusion and microvascular perfusion and quantify the corresponding parameters (i.e., $$$f$$$, $$$D$$$, and $$${D}^{*}$$$) in the brain. Conventional approach for resolve these parameters relies fitting the bi-exponential model from multi-b-value diffusion MRI data (typically ≥ 10 b-values), which requires a relatively lengthy acquisition. Such acquisition can be challenging for the fetal brain due to excessive motion of the fetus and maternal body. Deep learning models can be used to accelerate diffusion MRI acquisition for DTI, DKI, and fiber-tracking applications using a subset of the Q-space data². However, the common CNN-based deep learning is not related to the biophysical model, and therefore, is hard to be interpreted. Here, we combined the sparsity coding with deep learning to develop a novel model-driven sparsity coding deep neural network (SC-DNN), which took the advantages of the high-dimensional feature presentation by deep networks while incorporating the underlying bi-exponential model for estimating IVIM parameters in the fetal brain.

Methods

Sparsity coding:The IVIM model can be defined as:
$$\begin{equation}S_{b}/S_{0}=\left[(1-f)e^{-bD}+fe^{-bD^{*}}\right]\tag{1}\end{equation}$$
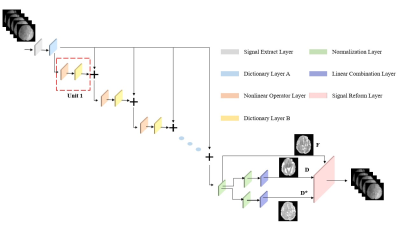
A model-based neural network is typically designed to unfold the optimization process of the model^3,4. But bio-exponential model cannot be directly unfolded due to its non-linearity. Therefore, we propose to use sparsity coding to linearize the IVIM model by constructing a dictionary matrix and a coefficient matrix, similar to that in AMICO⁵. In sparse coding, the IVIM signal model can be reformulated as below:
\begin{equation}y=\varphi_{n}x\tag{2}\end{equation}
where, $$$\varphi_{n} $$$ is a dictionary matrix ($$$\mathbb{R}^{2j\times1}$$$) and $$$x$$$ is a coefficient matrix. $$$\varphi_{n} $$$ and $$$x$$$ can be constructed as below:
$$\begin{equation}{\varphi}_{{n}}=\left[{\varphi}_{n}^{{D}}{\varphi}_{n}^{{D}^{*}}\right]\tag{3}\end{equation}$$
$$\begin{equation}x=\left[x_{1-f},x_{f}\right]^{T}\tag{4}\end{equation}$$
where, $$${\varphi}_{n}^{D}$$$ corresponds to the discretized $$$D$$$ and $$${\varphi}_{n}^{{D}^{*}}$$$ is the discretized $$${D}^{*}$$$. $$$x_{1-f}$$$ corresponds to the fraction of the tissue component ($$$D$$$) and $$$x_{f}$$$ is the fraction of perfusion component ($$${D}^{*}$$$), both of which are sparse. $$$\left[x_{1-f},x_{f}\right]^{T}$$$ are normalized between 0-1. Then $$$D$$$ and $$${D}^{*}$$$ can be obtained through the linear combination of the two matrices:
$$\begin{equation}{f}=\sum{x}_{{f}}\tag{5}\end{equation}$$
$$\begin{equation}D=\frac{\sum D_{j} x_{f}^{j}}{\sum x_{f}^{j}}\tag{6}\end{equation}$$
$$\begin{equation}{D}^{*}=\frac{\sum{D}_{j}^{*} x_{1-f}^{j}}{\sum x_{1-f}^{j}}\tag{7}\end{equation}$$
Network construction: In this optimization of the linearized model (Eq [2]), the objective equation is written as a $$$\ell_{0}$$$-norm regularized least squares as shown below:
$$\begin{equation}\min _{x}\left\|y-\varphi_{n} x\right\|_{2}^{2}+\beta\|x\|_{0}\tag{8}\end{equation}$$
where, $$$\beta$$$ controls the sparseness of matrix $$$x$$$. Then the Iterative Hard Thresholding (IHT) method⁶ is used to solve this sparse reconstruction problem based on an iterative process as below:
$$\begin{equation}{x}^{n+1}={H}_{M}\left[\varphi_{n}^{H}{y}+\left({I}-\varphi_{n}^{{H}}\varphi_{n}\right){x}^{n}\right]\tag{9}\end{equation}$$
where, $$$H_{M}$$$ denotes the nonlinear operator. The network architecture is shown in Figure1.
Materials: The IVIM data were acquired on 3.0T Siemens Skyra scanner from ten normal pregnant women (gestational age 23-33 weeks) under IRB approval. Diffusion-weighted gradients were applied in three directions at 10 b-values of 0, 10, 20, 50, 100, 150, 200, 300, 500 and 600s/mm², with the following acquisition parameters: TR/TE = 4200/89ms, in-plane resolution= 2×2 mm, matrix size = 124×124, field of view = 260×260 mm, 20 slices with a slice thickness of 4 mm.
Training and testing: Diffusion signals from 5 of the 9 b-values (20,50,200,300,600)were extracted as input for each voxel, and $$$[f, D, {D}^{*}]$$$ maps fitted with a Baysian method from all b-values were provided as outputs. Here, we chose Adam as the optimizer, and the learning rate was set to 0.0001, with total epochs of 50 and batch size of 512. As the network can be hardly converged, we used the warm-up method^7,8 in the first 5 epochs, and the learning rate decayed after 50 epochs. Since training was performerd in a voxelwise manner, we finally had 245760 data points (from 12 subjects) for training, 20% for validation and 20% for testing.

Results

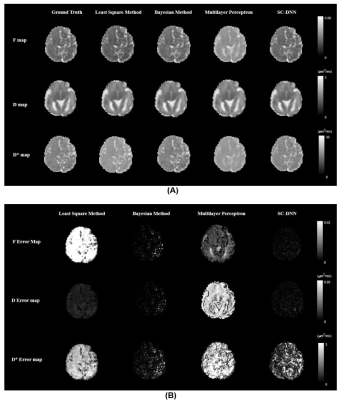
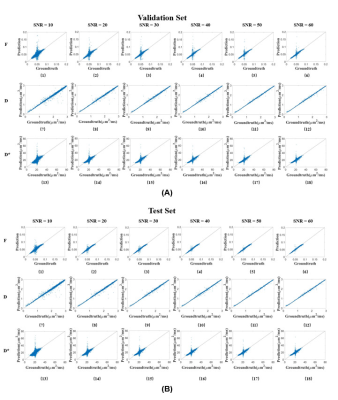
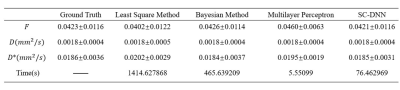
We first performed simulation to test the accuracy and robustness of SC-DNN by adding rician noise to the simulated signals. As shown in Figure 1, SC-DNN was robust to noise up to SNR of 30, and the estimations became noisier as SNR further decreased, but were still close to the groundtruth. The performance of different IVIM fitting methods is compared in Table 1. Compared with the ground truth, the SC-DNN outperformed the least square model in terms of both accuracy and time consumption and achieved comparable performance with only 17% time costing relative to the Bayesian model. Furthermore, the SC-DNN was more accurate than Multilayer Perceptron in $$${D}^{*}$$$ estimation. The $$$f$$$, $$$D$$$, and $$${D}^{*}$$$ maps obtained from different methods are visualized in Figure 2(a), and Figure 2(b) gives the residual map between the estimated maps and the ground truth. It is shown that SC-DNN can reach comparable performance with Bayesian method and performed better than Multilayer Perceptron.

Discussion and Conclusion

In this study, we showed that the proposed SC-DNN achieved reliable IVIM parameters estimation with only a subset of the rawdata, and thus could be potentially used to accelerate IVIM acquisition. This is particularly important for applications that are subject to motion artifacts, such as fetal and placental IVIM, and the shortened acquisition also improves the patient comfortness for pregnant patients. The proposed model-driven network incorporated the underlying IVIM model in the network design, which enhances its performance, e.g., higher performance than Multilayer Perceptron. Further work should compare the SC-DNN with regular CNN, and test its generalizability on patient data or data acquired from other centers.

Acknowledgements

This work is supported by the Ministry of Science and Technology of the People’s Republic of China (2018YFE0114600), National Natural Science Foundation of China (61801424 and 81971606).