Intoduction

The large amplitude and long duration of diffusion sensitizing gradients make Diffusion Weighted Imaging (DWI) sensitive to movements. “Intra-scan” rotations between excitation and readout can disturb the gradient balance of a DWI sequence, which can push the signal (echo) outside of the sampled k-space, and cause signal loss or dropouts [1]. Gradient balances can be restored using prospective motion correction (PMC) [2]. Here, we applied multiple updates to the gradient matrix within a single-shot monopolar diffusion sequence. Updates were provided by a fast (60 frames/second) MR-compatible optical head tracking system. As noted previously [3], intra-scan PMC updates were able to recover signals otherwise lost. However, residual gradient moments with PMC were larger than anticipated, showing an unusual bimodal dependence on angular velocities. This bifurcation was found to be caused by the discretized nature and asynchronous application of motion updates within the pulse sequence.

Theory

The gradient moment imbalance (differential moments with and without motion) $$$\Delta\vec{M}$$$ due to rotation while diffusion gradients $$$\vec{G}^{DW}(t)$$$ play, is $$$\Delta\vec{M}=\int_{0}^{T}[\hat{1}-\hat{R}^{-1}(t)]\vec{G}^{DW}(t)dt$$$, where $$$\hat{R}(t)$$$ is the time dependent rotation matrix (T<TE). Assuming a rotation $$$\theta(t)$$$ about the y-axis yields:
$$\begin{equation}
\begin{bmatrix} \Delta M_{x} \\ \Delta M_{y} \\ \Delta M_{z} \end{bmatrix} = \int_{0}^{T}
\begin{bmatrix} 1-\cos(\theta(t)) & 0 & \sin(\theta(t)) \\ 0 & 0 & 0 \\ -\sin(\theta(t)) & 0 & 1-\cos(\theta(t))\end{bmatrix}
\begin{bmatrix} G_{x}^{DW} \\ G_{y}^{DW} \\ G_{z}^{DW} \end{bmatrix} dt
\end{equation}$$
with $$$\theta(0)=0$$$. Since the head can only rotate a few degrees over ~100ms TE, we can perform a second-order Taylor expansion in $$$\theta$$$ and approximate $$$\theta(t)\approx\omega_{r}t+0.5\alpha_{r}t^2$$$, to obtain
$$\begin{array}{l}\Delta M_{x} \approx \omega_{r}\int_{0}^{T}G_{z}^{DW}(t)tdt +\frac{1}{2}\int_{0}^{T}(\omega_{r}^2G_{x}^{DW}(t)+\alpha_{r}G_{z}^{DW}(t))t^2dt \\
\Delta M_{z} \approx -\omega_{r}\int_{0}^{T}G_{x}^{DW}(t)tdt +\frac{1}{2}\int_{0}^{T}(\omega_{r}^2G_{z}^{DW}(t)-\alpha_{r}G_{x}^{DW}(t))t^2dt
\end{array}$$
Hence, head rotation during diffusion gradient lobes creates:

• A first-order gradient moment, proportional to the rotational velocity and a second-order gradient moment, proportional to the rotational acceleration, perpendicular to the diffusion gradient and rotation axis.
• A second-order gradient moment, proportional to the squared rotational velocity, in the diffusion gradient axis.

Methods

We simulated the residual gradient moment in the readout direction (x-axis) with a diffusion gradient in phase encoding direction (z-axis). Since gradient moments define k-space, residual moments offset the echo from the k-space center. The offset is (to first order) proportional to the rotational velocity during the diffusion interval.
We tested our PMC scheme on a gel-filled spherical phantom with a rigidly attached tracking marker. Motion was tracked by an MR-compatible camera. The phantom was rotated quasi-sinusoidally about y-axis during the DWI monopolar sequence (TE/TR=80/500ms, b=1000s/m², diffusion sensitization in phase encode (z-axis), FOV=300mm, BW=2170Hz/Px, matrix=128x64, 5mm coronal, 216 repetitions). Since the phantom movement and scanning process are asynchronous, each DWI acquisition reflects a random (but known) rotational velocity. The echo-center k-space shift is used to determine the residual moment ($$$\Delta k_{x}^{max}=\gamma\Delta M_{x}$$$). The effectiveness of the proposed PMC scheme is quantified by the reduction in residual gradient moments relative to simulations.

Results

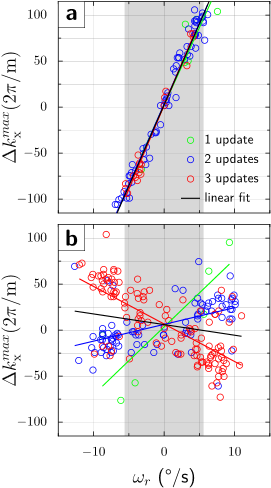
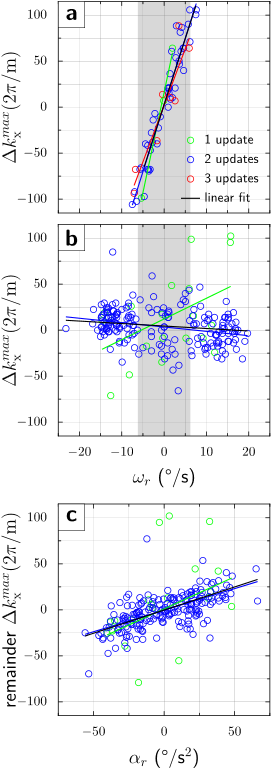
Simulation. Diffusion gradient amplitude and timing are from the manufacturer's monopolar sequence (Fig.1a). The object and gradient axes gradually misalign due to the object’s rotation during the diffusion preparation interval, and first- (Fig.1b) and second-order (Fig.1c) residual moments are accrued. The simulation used $$$\omega_{r}=13^{\,\circ}/\mathrm{s}$$$ and $$$\alpha_{r}=60^{\,\circ}/\mathrm{s}^2$$$, which represent moderately fast human head rotations. For the given EPI parameters, velocities $$$|\omega_{r}|>6^{\,\circ}/\mathrm{s}$$$ [residual moment $$$\gamma\Delta M_{x}=111(2\pi/\mathrm{m})$$$] cause signal dropout. If a gradient realignment (motion update) is applied immediately prior to the refocusing pulse, the first-order moments and therefore echo-center offsets from k-space center are substantially decreased. However, the second-order residual moment is only partially corrected, causing residual k-space offsets.

Experiment. Graphs in Figs.2,3 show the dependence of k-space shifts upon rotational velocities. Without PMC, only half of repetitions $$$|\omega_{r}|<6^{\,\circ}/\mathrm{s}$$$ remain within the sampling window (Figs.2a,3a). Conversely, with PMC, only 4% of repetitions dropped out (Figs.2b,3b). However, the graph with PMC enabled shows two sub-populations (Fig.2b). We hypothesized that this bifurcation is caused by the discrete number of motion updates in the first TE/2 period. Specifically, at TE/2 = 40ms and 60 frames/second tracking rate (~17ms inter-packet time), either 2 or 3 tracking packets may arrive between the excitation and refocusing pulse. The gradient rotation applied is under-compensated for 2 updates, but over-compensated for 3 updates. Thus, matching TE/2 to a multiple of the inter-packet time (17ms) should eliminate the bifurcation. This was confirmed experimentally at TE=68ms (TE/2=34ms=2*17ms), where generally 2 motion updates are applied between excitation and refocusing (Fig.3b). Also, since the variance due to 2 sub-populations is eliminated, an effect of rotational accelerations becomes noticeable (Fig.3c, second-order moment).

Conclusion

Intra-sequence motion updates during DWI can markedly reduce signal dropouts during fast head movements, and careful selection of TE values might further decrease motion sensitivity. A secondary benefit is the realignment of excitation and refocusing slices.