INTRODUCTION

Diffusion MRI data have been mostly acquired with single-shot echo-planar-imaging (EPI) because single-shot techniques are fast and robust against motion during diffusion encoding, particularly against pulsatile brain motion¹. However, this approach is limited to the spatial resolution that can be achieved with just a single readout. Higher resolution is afforded by multiple-shot, segmented acquisitions. These, however, require special reconstruction schemes that correct for shot-to-shot phase variations due to motion during diffusion encoding. Multiplexed sensitivity-encoding (MUSE)² relies on separate parallel imaging reconstruction of individual segments to estimate phase maps and subsequently obtain a joint image from all segments. The phase estimation is challenging when readouts are highly segmented and thus highly undersampled individually, causing strong g-factor penalty and increased artifact due to ill-conditioning. Against this background, an interesting option for highly segmented diffusion imaging is spiral acquisition, which has recently been found to offer more benign g-factor behavior than EPI³.
On this basis, the present work studies the feasibility of highly segmented diffusion imaging with spiral acquisition and MUSE reconstruction. To stabilize reconstruction, we additionally explore the utility of joint optimization of phase biases and image content.

METHODS

Theory: Reconstruction of multi-shot diffusion data can be formulated as the minimization of
$$L = ||m-E\Phi O||_2^2 + \lambda||\nabla^2 \phi_{vc}||_2^2. \qquad \textrm{[1]}$$
by varying the object vector O [N²×1] and the vector $$$\phi_{vp}$$$ [n_sN²×1] of phase biases for all shots, given the measured signal m [n_sn_kn_c×1], the block diagonal encoding matrix E [n_sn_kn_c×n_sN²], which incorporates coil sensitivities, the k-space trajectory, and B₀ inhomogeneity. $$$\Phi$$$ of size [n_sN²×N²] is a stack of diagonal matrices with entries $$$e^{i\phi_{vp,(j,x)}}$$$, $$$\phi_{vc}$$$ of size [n_sN²×1] lists the same phasors in a vector, and λ is a regularization parameter. n_s, n_k, n_c, and N² represent the number of shots, sampling points, coil elements and image voxels, respectively. In Eq. [1], the first term ensures data fidelity and the second penalizes roughness. The derivatives of the loss function with respect to O and $$$\phi_{vp}$$$ are
$$\frac{\partial L}{\partial O}=-2\Phi^HE^H (m-E\Phi O)\qquad \textrm{[2.1]}$$
$$\frac{\partial L}{\partial \phi_{vp}}=2Re\left[i \cdot{} diag\left(\left(\Phi O\right)^H\right)E^H\left(m-E\Phi O\right)\right]+2Re\left[-i \cdot{} diag\left(\phi_{vc}^H\right)\left(\nabla^2\right)^H)\nabla^2\phi_{vc}\right]. \qquad \textrm{[2.2]}$$

Data Acquisition: One healthy volunteer was scanned under local ethics approval with a 3T Philips Achieva scanner and gradients operated in parallel mode (G_max=80mT/m, slew-rate_max=100mT/m/ms). A 16ch receive-only brain array with 16 integrated ¹⁹F NMR probes (NeuroCam, Skope MR Technologies, Zurich, Switzerland) was employed to collect MRI raw data and concurrently monitor magnetic field evolution. For mapping B₀ and coil sensitivities, multi-echo GRE images (TE/ΔTE=2.3/1.15ms) were acquired. Four spiral diffusion datasets (b=1000s/mm²) were acquired with varying number of shots (n_s=4,8,12,16) and readout durations (T_RO=54,27,18,14ms) at the resolution of 0.8×0.8×2.0mm³.

Image Reconstruction: Diffusion datasets were reconstructed using the MUSE method. To stabilize reconstruction upon strong segmentation, the loss (Eq. [1]) was minimized by strict gradient descent, using the analytical gradients (Eq. [2]). As Eq. [1] is non-convex, appropriate initialization is important. The MUSE result was used to initialize O and $$$\phi_{vp}$$$. In each iteration, a line search was performed along the gradient direction, updating O and $$$\phi_{vp}$$$ simultaneously.
From concurrently monitored phase evolutions of NMR probes, 3^rd-order phase expansions in terms of spherical harmonics were determined, including 2^nd-order concomitant field correction⁴. These phase expansions, B₀ and sensitivity maps were used to set up the encoding matrix in all reconstructions⁵.

RESULTS

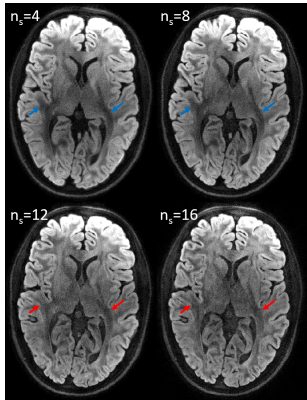
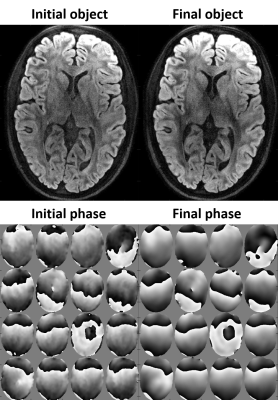
Fig. 1 shows multi-shot diffusion-weighted images (DWIs) reconstructed using the MUSE algorithm. Even at high segmentation, high image quality was obtained. This is remarkable considering that reconstruction from individual shots is vastly ill-conditioned in these cases. Nevertheless, the DWIs with 12- and 16-fold segmentation exhibit less and partly altered diffusion contrast (blue vs. red arrows). As shown in Fig. 2, the proper contrast strength and structure were recovered by joint optimization of phase biases and image content.

DISCUSSION

Multi-shot DWIs with highly segmented spiral readouts were successfully reconstructed with high image quality, resolution and high SNR even without averaging and not requiring navigator data. The MUSE method provided high image quality even with strong segmentation. This is attributed to the relatively benign scale and spatial structure of the g-factor for spiral readouts as well as to the accuracy of the signal model (readout trajectories, B₀ and sensitivity maps). Nonetheless, slight alteration of diffusion contrast was observed in the highly segmented images. This effect was overcome by weighted minimization of signal model violation and roughness of phase biases. Unlike MUSE, joint estimation of image content and phase bias is not prone to error propagation from ill-conditioned phase estimates based on single shots.

CONCLUSION

Spiral readouts readily permit highly segmented diffusion imaging without navigation. MUSE processing yielded robust image reconstruction up to intermediate segment counts. Joint optimization of phase biases and image content expanded the feasible range up to 16 segments. Expanded feasibility of segmented diffusion scanning is a promising prospect in that it reconciles high resolution with intrinsic limits on readout duration while maintaining the time efficiency of standard scanning without navigation or segmentation in the frequency encoding direction.

Acknowledgements

Technical support from Philips is gratefully acknowledged.