1319
Distortionfree multishot 3D diffusion weighted turbo spin echo imaging using cartesian spiral acquisition and data rejection1Department of Radiotherapy, University Medical Center Utrecht, Utrecht, Netherlands, 2Computational Imaging Group for MRI diagnostics and therapy, Centre for Image Science, Utrecht, Netherlands
Synopsis
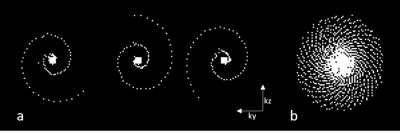
In this work a multishot 3D turbo spin echo (TSE) sequence is combined with a diffusion preparation module and a modified implementation of the cartesian spiral (CASPR) k-space sampling pattern. CASPR samples the center of k-space in each shot, providing redundancy and enabling self-navigated identification of corrupt data.
Using low resolution reconstructions per shot, weights are assigned for each shot enabling a soft-weighted compressed sense reconstruction.
Results are obtained in a phantom and healthy volunteers, demonstrating the feasibility in acquiring undistorted 3D diffusion images.
Introduction
Diffusion weighted imaging (DWI) can visualize differences in cell density due to its sensitivity to water mobility, providing images with high contrast between tumors and their surroundings. In radiotherapy for example, DWI can be used in the treatment planning phase to determine treatment volumes and to monitor treatment response. With the introduction of hybrid MR-Linac systems [1], even daily DWI can be acquired. The use of DWI in this setting requires high geometric fidelity: conventional single-shot echo-planar-imaging might be insufficient here [2]. Ideally, a 3D sequence is used.Diffusion sensitization can be applied to multishot 3D sequences using a diffusion preparation module [3,4,5]. However, in multishot DWI, phase inconsistencies between different shots due to motion are a known issue and can severely degrade image quality. Typically, there are a few severely corrupted shots while the majority of shots will be consistent. Identifying the motion corrupted data could be key in resolving the multishot reconstructions.
In this work a multishot 3D turbo spin echo (TSE) sequence is combined with a diffusion preparation module and a modified implementation of the cartesian spiral (CASPR) k-space sampling pattern [6,7]. CASPR samples the center of k-space in each shot, providing redundancy and enabling self-navigated identification of corrupt data.
Methods
Image acquisitionA diffusion prepared TSE sequence was implemented, using magnitude stabilization [3,8]. The CASPR k-space trajectory was adapted to sample the 5x5 center of k-space at the start of each shot, the spiral arms were rotated with the golden angle with each shot (figure 1).
Image reconstruction
The acquired k-space data was exported and processed using ReconFrame (Gyrotools, Zurch, CH).
First, the data was cropped to a lower resolution and reconstructed for each shot using a low-rank regularization over the shots [9].
Then, using the low resolution complex images, for each shot the normalized root-mean-square-error (nRMSE) was calculated as a measure of shot quality [10]. The reference shot was determined iteratively, choosing the shot which yielded the lowest overall error.
The nRMSE were used to assign weights to each shot: shots with high nRMSE were rejected.
After the soft-weighted shot combination, a weighted compressed sense reconstruction with spatial total variation regularization was performed using the Berkeley Advanced Reconstruction Toolbox [11].
Phantom experiments
A phantom was scanned on a 1.5T scanner (Philips Ingenia, Best, The Netherlands) with a 15 channel head coil to test the geometric fidelity and diffusion attenuation. A regular cartesian acquisition was done as no phase inconsistencies are expected with the phantom. Acquisition voxel size: 2 mm3; FOV: 256x256x256; Matrix: 128x128x128; TR/TE = 1000/33 ms; TSE factor = 90 (3 startup echoes); acquisition bandwidth: 1436 Hz; diffusion preparation TE: 90 ms; b-values: 0-200-400-600-800 s/mm2; 30 seconds per volume, total acquisition time 6m32s.
In-vivo experiments
Data was acquired in two healthy volunteers on the same system. Diffusion weighting was applied along 3 orthogonal directions, which were averaged after reconstruction to obtain an isotropic diffusion weighted image. The 3D TSE readout used the center-out CASPR sampling, with undersampling factor 2. Scans were acquired at 2 different resolutions:
- 3 mm3, FOV: 220x220x200; Matrix: 72x73x66; TR/TE = 1500/19.7 ms; TSE factor = 100 (3 startup echoes); shots = 19; acquisition bandwidth: 2445 Hz; diffusion preparation TE: 122 ms; b-values: 0-500 s/mm2; 29 seconds per volume, total acquisition time 1m58s.
- 2 mm3, FOV: 220x220x200; Matrix: 112x110x100; TR/TE = 1500/24 ms; TSE factor = 100 (3 startup echoes); shots = 42; acquisition bandwidth: 1641 Hz; diffusion preparation TE: 98 ms; b-values: 0-500-1000 s/mm2; 65 seconds per volume, total acquisition time 7m35s.
Results and discussion
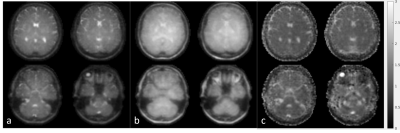
Figure 2 shows the results of the phantom experiments. No distortions are visible, as expected with the 3D TSE readout. The signal attenuation is consistent along the three orthogonal axes and different diffusion weightings. This is also reflected in the ADC values (EPI reference not shown).In figure 3 an example of the low resolution reconstructions per shot is given for and in-vivo acquisition. These are the 19 shots of a single diffusion direction at b=500 s/mm2. The majority of shots are consistent, but several corrupted ones can be observed.
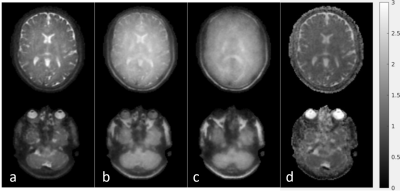
The result of the soft-weighted compressed sense reconstruction is shown in figure 4. In figure 5, a higher b-value was also included (b=1000 s/mm2) at 2 mm3 isotropic resolution. The increased spatial resolution and lack of distortion artefacts can be observed. However, at b=1000 s/mm2, the increasing phase inconsistencies between the different shots cause the reconstruction to become blurred. Here, the weighted reconstruction can insufficiently correct these errors. To resolve these errors, the currently proposed sequence could be complemented with a 3D phase-informed reconstruction [10,12,13] which could use the low resolution reconstructions as a initial phase estimate per shot.
Conclusion
This work demonstrates the feasibility of a multishot 3D diffusion weighted TSE sequence with a redundant cartesian spiral sampling pattern and data rejection to improve robustness against phase inconsistencies between different shots.Acknowledgements
No acknowledgement found.References
[1] Lagendijk JJ, Raaymakers BW, van Vulpen M. The magnetic resonance imaging-linac system. Semin Radiat Oncol. 2014 Jul;24(3):207-9. doi: 10.1016/j.semradonc.2014.02.009.
[2] Schakel T, Hoogduin JM, Terhaard CH, Philippens ME. Diffusion weighted MRI in head-and-neck cancer: geometrical accuracy. Radiother Oncol. 2013 Dec;109(3):394-7. doi: 10.1016/j.radonc.2013.10.004.
[3] Zhang Q, Coolen BF, Versluis MJ, Strijkers GJ, Nederveen AJ. Diffusion‐prepared stimulated‐echo turbo spin echo (DPsti‐TSE): an eddy current‐insensitive sequence for three‐dimensional high‐resolution and undistorted diffusion‐weighted imaging. NMR Biomed. 2017; 30(7): e3719.
[4] Roccia, E, Neji, R, Benkert, T, Kiefer, B, Goh, V, Dregely, I. Distortion‐free 3D diffusion imaging of the prostate using a multishot diffusion‐prepared phase‐cycled acquisition and dictionary matching. Magn Reson Med. 2020; 85: 1441– 1454. doi.org/10.1002/mrm.28527
[5] Gao YU, Han F, Zhou Z, et al. Multishot diffusion‐prepared magnitude‐stabilized balanced steady‐state free precession sequence for distortion‐free diffusion imaging. Magn Reson Med. 2019;81:2374‐2384.
[6] Prieto C, Doneva M, Usman M, Henningsson M, Greil G, Schaeffter T, et al. Highly ef- ficient respiratory motion compensated free-breathing coronary MRA using golden- step Cartesian acquisition. J Magn Reson Imaging 2015;41:738–46
[7] Bruijnen T, Akdag O, Bruel C, Stemkens B, Schakel T, Lagendijk J, van den Berg C and Tijssen RHN; 2020; Free-breathing 3D T2-weighted TSE using Cartesian acquisition with rewinded spiral profile ordering (rCASPR) for abdominal radiotherapy; in Proc. ISMRM 28.
[8] Van AT, Cervantes B, Kooijman H, Karampinos DC. Analysis of phase error effects in multishot diffusion-prepared turbo spin echo imaging. Quant Imaging Med Surg. 2017;7(2):238-250. doi:10.21037/qims.2017.04.01
[9] Hu, Y, Levine, EG, Tian, Q, et al. Motion‐robust reconstruction of multishot diffusion‐weighted images without phase estimation through locally low‐rank regularization. Magn Reson Med. 2019; 81: 1181– 1190. doi.org/10.1002/mrm.27488
[10] Steinhoff M, Nehrke K, Mertins A, Börnert P. Segmented diffusion imaging with iterative motion-corrected reconstruction (SEDIMENT) for brain echo-planar imaging. NMR Biomed. 2020 Dec;33(12):e4185. doi: 10.1002/nbm.4185.
[11] Uecker M, Tamir J, Ong F, Holme C, and Lustig M. (2017, June 23). BART: version 0.4.01 (Version v0.4.01). Zenodo. http://doi.org/10.5281/zenodo.817472
[12] Chu M‐L, Chang H‐C, Chung H‐W, Truong T‐K, Bashir MR, Chen N‐k. POCS‐based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): A general algorithm for reducing motion‐related artifacts: POCSMUSE Reconstruction for Motion Artifact Removal. MRM. 2015;74(5):1336‐1348.
[13] Guo H, Ma X, Zhang Z, Zhang B, Yuan C, Huang F. POCS‐enhanced inherent correction of motion‐induced phase errors (POCS‐ICE) for high‐resolution multishot diffusion MRI: High Resolution Multishot DWI without Navigator. MRM. 2016;75(1):169‐180.
Figures