Purpose

The purpose of this study was to demonstrate the feasibility of a novel framework in which a deep neural network is trained to directly convert images obtained with single transmission (sTx) into their pTx version with improved image quality.

Methods

Training dataset
Our training dataset was built on our previous data acquisition aimed at demonstrating the utility of pTx for high-resolution, whole-brain diffusion weighted imaging (dMRI) at 7T¹. Specifically, it consisted of data acquired on 5 healthy subjects using a 7T scanner (Siemens, Erlangen, Germany). For each subject, the data comprised a pair of matched, 1.05-mm Human-Connectome-Project (HCP)-style dMRI sets: one obtained using sTx and the other pTx. Both image sets consisted of 36 preprocessed volumes (including 4 b0 images and 32 diffusion-weighted images with b-value of 1000 s/mm² (b1000)), leading to a total of 18,000 samples (5 subjects × 100 slices × 36 volumes) in our training dataset.
Deep convolutional neural network
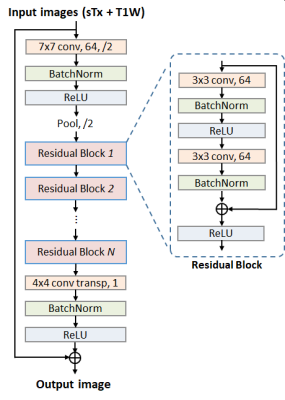
We constructed a deep residual neural network (ResNet)² to predict pTx images given sTx ones owing to its ease of training and its demonstrated utility for various imaging applications^3-5. Compared with the original ResNet structure, our ResNet (Fig. 1) had three modifications: 1) constant (instead of varying) matrix size (1/4 of the input) and channel number (64) throughout all residual blocks, 2) additional skip connection between input and output for improved prediction performance, and 3) transposed convolutional (instead of a fully-connected) layer for the last layer. Further, our ResNet took T1-weighted MPRAGE images as additional input since this was shown in our pilot study to result in better prediction accuracy. The loss function was formulated to measure the mean squared error (MSE) between the output of ResNet and the pTx diffusion images. The minimization was conducted using the Adam algorithm⁶.
The network was implemented using the Flux package in Julia⁷ and was trained on a Linux workstation using one NVIDIA TITAN RTX GPU. The total training time was ~30 minutes while the inference time for one image slice was ~35 ms.
Model selection and evaluation
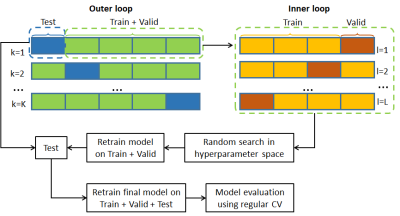
We conducted cross-validation (CV) (Fig. 2) for model selection and evaluation. In model selection, a nested 5-fold CV (with dataset split into 3/1/1 for training/validation/testing and each fold comprising data of a single subject) was performed to tune relevant hyperparameters including the number of residual blocks, number of epochs, mini-batch size, and learning rate initialization LR₀/decay factor DF/decay steps DS (with learning rate at ith epoch: $$$LR_{i}=LR_{0}\cdot{e^{-DF\cdot{floor(\frac{i-1}{DS})}}}$$$). The hyperparameter tuning was carried out using a random search where 20 points in the hyperparameter space were randomly sampled. The hyperparameter set providing the best prediction performance was selected to form the final model. In model evaluation, the generalizability of the final model was estimated using a regular 5-fold CV (with dataset split into 4/1 for training/testing).

Results

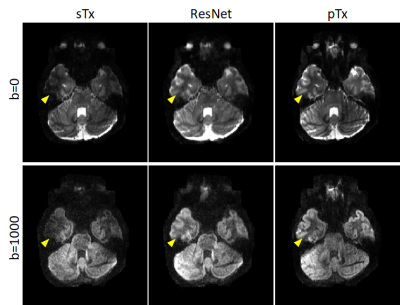
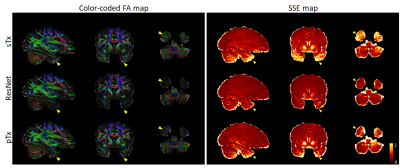
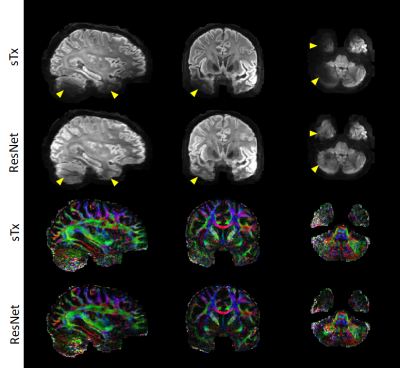
Per the results from nested CV, our final model was created using the following hyperparameters: 10 residual blocks, 30 epochs, mini-batch size=32, and learning rate initialization/decay factor/decay steps=10^-4/0.15/8. The generalizability of the final model was found to be high, with the mean test loss across folds being as low as ~8.7×10^-5. Further quantitative analysis on the outcomes of the 5-fold CV revealed that the final model would improve the image quality and DTI performance in comparison to sTx, reducing RMSE and SSE (averaged across whole brain and all subjects) by ~23% (0.27 vs 0.35) and by ~44% (0.32 vs 0.57), respectively.
These improvements were further confirmed by inspecting individual images: the signal dropout in the temporal pole observed with sTx was effectively recovered by using our final model and the predicted pTx images were comparable to those obtained with pTx (Fig. 3). Such image recovery in turn translated into improved DTI (Fig. 4), producing color-coded FA maps similar to those obtained with pTx and reducing SSE in the lower brain regions.
Encouragingly, the use of our final model (trained on all our data of 5 subjects) to predict pTx images for a new subject from the 7T HCP database appeared to substantially enhance the image quality by effectively restoring the signal dropout observed in the lower brain regions (e.g., the temporal pole and cerebellum), producing color-coded FA maps with largely reduced noise levels in those challenging regions.

Discussion and Conclusion

We have introduced and demonstrated a deep-learning approach that can directly map sTx images to their pTx counterparts. Our results using 7T high-resolution whole-brain dMRI show that our approach can substantially improve image quality by effectively restoring the signal dropout present in sTx images, thereby improving the downstream diffusion analysis. As such, our approach shows great potential to become a user-friendly pTx workflow that can provide pTx-style image quality even when pTx resources (including pTx expertise, software or hardware) are inaccessible on the user side.
In the future, we will fully evaluate the prediction performance of our method with a focus on regions with extremely low SNR and study how our method may work when there is pathology. In addition, we will investigate how the prediction accuracy can be improved by increasing training data and refining the network structure, and by exploring the utility of other machine learning frameworks (e.g., GAN⁸).

Acknowledgements

The authors would like to thank John Strupp, Brian Hanna and Jerahmie Radder for their assistance in setting up computation resources. This work was supported by NIH grants U01 EB025144, P41 EB015894 and P30 NS076408.