Introduction

Functional Connectomes (FCs), estimated from functional MRI, have been shown to possess a reproducible subject fingerprint¹, which can be improved by maximizing differential identifiability across repeated sessions (test-retest) by using a group-level principal component analysis (PCA) decomposition method^2,3. Here, we explore the application of this framework to T1 anatomical brain images to enhance test-retest reliability with the goal of understanding the non-physiological differences present in repeated MRI measures of a subject, both within and across scanners, which is necessary to improve image harmonization in longitudinal and multi-site studies.

Methods

This study utilized MRI data from 18 undergraduate and graduate students (9 female, age 18-28). For each subject, two T1 structural images were taken (test, retest) on the same day. Scans were conducted on a 3T GE Discovery MR750 with 32-channel brain array (Nova Medical) and used a T1-weighted protocol with 3D fast spoiled gradient recalled echo sequence (TR/TE = 5.7/1.976 msec; flip angle = 73°; 1 mm isotropic resolution).
All images were processed using AFNI⁴ and FSL⁵ commands as described by Bari et al.³, registered to a common brain atlas⁶, and pooled to perform PCA. Registered images were subsequently reconstructed using varying numbers of principal components (PCs) to determine the subspace which produced maximum differential identifiability, 𝐼_{𝑑𝑖𝑓𝑓}. For each iteration we first construct an 18 x 18 identifiability matrix 𝐼, where 𝐼_𝑖,𝑗 is equal to the Euclidean distance between the subject 𝑖 test and the subject 𝑗 retest vectorized image. 𝐼_{𝑑𝑖𝑓𝑓} was computed as an average of two z-scores (associated with test and retest):

$$
I_{diff}=\frac{1}{2n}\sum\limits_{i=1}^n(\frac{\mu_{i,v}-I_{i,i}}{\sigma_{i,v}}+\frac{\mu_{i,h}-I_{i,i}}{\sigma_{i,h}})
$$

where 𝑛 is the number of subjects, 𝜇_𝑖 is the mean of entries in the 𝑖^𝑡ℎ row (indicated by ℎ) or column (indicated by 𝑣) of 𝐼, and 𝜎_𝑖 is the standard deviation of data in the 𝑖^𝑡ℎ row or column of 𝐼. Computation of both 𝜇_𝑖 and 𝜎_𝑖 exclude the 𝑖^𝑡ℎ entry 𝐼_𝑖,𝑖 of the corresponding row or column. The average distance between same-subject test and retest scans (D_self) and that between different-subject test and retest scans (D_others) were computed as:
$$
D_{self}=\frac{1}{n}\sum\limits_{i=1}^n{I_{i,i}}
$$
$$
D_{others}=\frac{1}{n^2-n}\sum\limits_{i=1}^n\sum\limits_{j=1}^n{I_{i,j}} - D_{self}
$$

To see if I_diff optimization helps remove noise from images, a noisy dataset was simulated by adding random Gaussian noise (𝜎_noise = standard deviation of all nonzero voxel intensities) to all images in the dataset. The PCA reconstruction method was then reapplied to the new noisy dataset.

Results

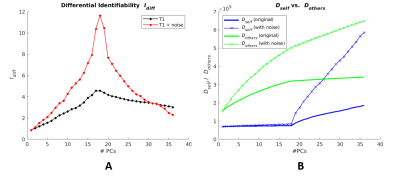
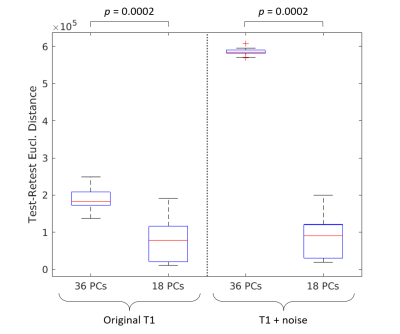
Reconstruction of both original and with-noise images at varying numbers of PCs results in variations in differential identifiability I_diff, with I_diff peaking at 18 PC reconstruction (Fig. 1A). The corresponding plots of D_self and D_others are shown in Fig. 1B.
The Euclidean distance (I_i,i) between same-subject test-retest images were grouped and compared between fully (36 PCs) and optimally (18 PCs) reconstructed images (Fig. 2), conducted separately for original images and images with added noise. A statistically significant difference (using Wilcoxon signed rank test) in medians was found between groups in both the original images (p=0.0002) and images with added noise (p=0.0002).

Discussion

Using group-level PCA decomposition of T1 images, we have shown that T1 images possess a test-retest fingerprint, and it can be enhanced by maximizing the differential identifiability (I_diff). The peak I_diff possible through PC reconstruction of the added-noise dataset is actually greater than that for the original images, which implies that the metric is dataset-specific and cannot necessarily be used to compare the quality of two separate datasets.
I_diff, in essence, reflects the gap between the metrics D_self and D_others. Fig. 1B illustrates that added noise results in notably higher D_others at 18 PCs, while it has little effect on D_self at 18 PCs. This causes a greater gap between D_others and D_self, hence the heightened I_diff peak observed for the noisy dataset. This observation implies that as the number of PCs is increased through the first 18 PCs, the increase in I_­diff stems from increasing distance between test-retest images from different subjects.
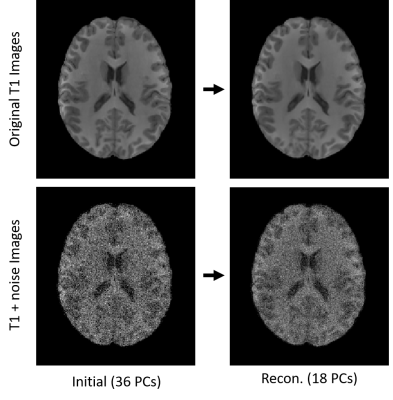
The analysis shown in Fig. 2 demonstrates that similarity between a subject’s test-retest images are significantly increased using the optimal PC reconstruction. Observation of the actual images related to 18 and 36 PC reconstruction (Fig. 3) shows that the optimal reconstruction results in decreased (though not completely removed) noise levels, implying that the method could be useful for improving reliability across repeated scans of the same subject. This method has potential to be useful in characterizing noise differences resulting from different scan sessions (both within and across scanners) through further analysis of the changes made during optimal I_diff reconstruction, but has drawbacks in that the resulting noise characteristics would be a function of the dataset used.

Conclusion

We demonstrate that differential identifiability can be maximized using reconstruction of images with an optimized number of PCs. This reconstruction results in significantly improved similarity between a given subject’s test-retest images and partially reduces noise present in the images, presenting potential future applications in reducing intersession noise. Deeper understanding of the I_diff metric requires concurrent observation of related metrics D_self and D_others.

Acknowledgements

This work was funded in part by the Purdue University Discovery Park Data Science Award "Fingerprints of the Human Brain: A Data Science Perspective”.