Introduction

NORDIC (1, 2) is a recently proposed framework for parameter free denoising using LLR PCA with hard thresholding (3), for elimination of signals that cannot be distinguished from thermal noise. NORDIC is proposed as an integrated sequential image-reconstruction and denoising technique using complex valued image reconstruction and an accurate knowledge of the g-factor. With NORDIC, a 2-4 fold increase in sensitivity can be observed (1, 2), with larger gains realizable when the relative contribution of thermal noise is high (low SNR) – where the need also is greatest.

In the original implementation, NORDIC was applied after parallel imaging reconstruction. This renders the NORDIC data incompatible with non-linear reconstruction methods, such as deep learning (DL), which have enormous tolerance to higher acceleration. To address this, we investigate the efficacy of using NORDIC prior to parallel image reconstruction, whereby preserving subsequent compatibility with DL based image reconstructions. We then compare this with the original approach of NORDIC in the context of fMRI.




When the fully sampled image is low-rank, then the aliased image will also be low-rank, since the matrix rank is subadditive, ie. rank(A+B) ≤ rank(A) + rank(B).

Methods

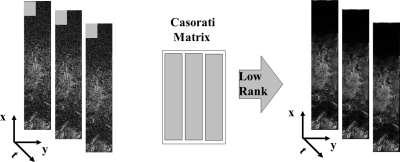
NORDIC Denoising Prior to Reconstruction

In NORDIC, a patch based Casorati matrix $$$ \bf{Y}=[y_1,⋯,y_{\tau},⋯,y_N] ∈\mathbb{C}^{(M×N)} $$$ is constructed such that each column $$$\bf y_{\tau} $$$ is composed of voxels in a fixed patch $$$ k_1 \times k_2 \times k_3 $$$ from each volume $$$ \tau \in \{1, \cdots , N \} $$$ in a series. The denoising problem in LLR is to recover the corresponding underlying data Casorati matrix $$$\bf X $$$ , based on the model $$ \bf Y = X + N $$ where $$$ N ∈ \mathbb{C}^{(M×N)} $$$ is additive Gaussian noise. In NORDIC, this is achieved by processing the image series such that the noise component is i.i.d. after reconstruction, and hard-thresholding at a level where signals cannot be distinguished from thermal noise based on non-asymptotic properties of random matrices (1).
However, when using non-linear reconstruction, the reconstruction noise is no longer Gaussian, rendering NORDIC incompatible. In this work, we proposed to perform NORDIC on the acquired aliased data directly using the same threshold selection methodology. For uniform undersampling patterns, where the patches fold onto other patches, this processing amounts to using LLR properties of a sum of Casorati matrices from different patches. Using the subadditivity of matrix rank, i.e. rank(A+B)≤rank(A)+rank(B), the aliased image patches will also have LLR properties if the fully-sampled image is amenable to LLR processing. NORDIC before image-reconstruction eliminates several processing steps of conventional NORDIC.

Data were acquired with a visual functional task on a 7T Siemens system, equipped with a 32 channel Nova coil. The scan was a 0.6 mm isotropic GE EPI with with 126 repetitions (+ 5 noise scans) covering 27 coronal slices with total scan duration 252 sec.
Parameters: FOV(ROxPE)=128x104mm2, R/L phase-encode. Matrix size=212x172, Phase-encoding undersampling=3, partial Fourier=6/8, TE/TR=30.4/2000ms, echo spacing=1.21ms.

The acquired data was pre-whitened and navigator-corrected. The undersampled k-space for each channel were Fourier-transformed along both the readout and phase-encoding directions. The thermal noise level was estimated in each channel from the edge of the readout.
The LLR PCA part from NORDIC (Fig 1.) was used independently for each acquired channel $$$ I_{ch}^{NORDIC, R>1}$$$ with a spatio:temporal ratio of 11:1, to obtain new undersampled images
$$ I_{ch}^{NORDIC, R>1} = I_{ch}^{Acq, R>1} -N $$
where $$$N$$$ is the estimated complex valued noise removed using NORDIC.

Results

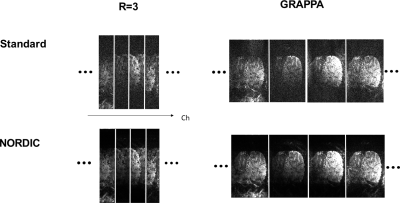
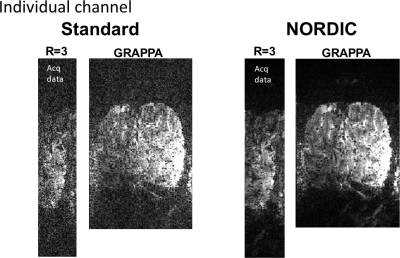
Figure 2, shows for R=3, the impact of denoising with NORDIC for 4 out of the 32 channels. The reduction in thermal noise is easily noted. For one of the channels, the noise-amplification effect in GRAPPA can be observed, which remains suppressed in the NORDIC processed data.
Figure 3, shows for R=3, the impact of denoising with NORDIC for 1 out of the 4 channels displayed in figure 2.
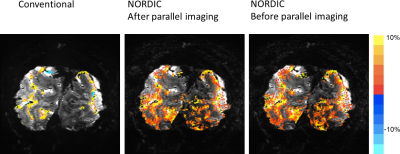
Figure 4, shows an activation map with the conventional acquisition, the recently introduced NORDIC post-processing, and the proposed NORDIC pre-processing.

Discussion/Conclusion

The proposed implementation of NORDIC prior to unaliasing is effective for integrating into nonlinear reconstruction pipelines (e.g. DL) and is demonstrated here for linear image reconstruction to establish feasibility. NORDIC pre-processing requires the whole series and is not compatible with real-time imaging, but works equally well for simultaneous multi slice (SMS)/Multiband (MB) imaging with and without phase-encoding undersampling.

The proposed NORDIC processing is effective for integrating into reconstruction pipelines that utilize the acquired MRI data, and is demonstrated for a linear image reconstruction. NORDIC pre-processing requires the whole series and is not compatible with real-time imaging, but works equally well for SMS imaging with and without phase-encoding undersampling.

The proposed NORDIC implementation prior to parallel imaging reconstruction is as effective for improving fMRI as the NORDIC implementation after GRAPPA unaliasing(1). The NORDIC prior to GRAPPA is applied for each channel individually. Further investigation on the effects of using multiple channels jointly for denoising is warranted.

NORDIC applied to measured raw k-space is compatible with non-linear or DL image reconstructions. Further investigation into point-spread function correction, eddy-current correction and channel specific processing are warranted. Coil-combinations with STARC (4) and alternatives to either RSOS or SENSE1(5) need to be evaluated.

Acknowledgements

Acknowledgement. U01 EB025144, P41EB027061; P30 NS076408, CAREER CCF-1651825, R01HL153146, R01 MH111447