Introduction

Quantification using 3D-T_1ρ MRI of the brain finds a number of biomedical applications such as multiple sclerosis, Alzheimers’ and stroke (1). A big drawback of current 3D-T_1ρ techniques is the MRI acquisition time required to obtain the data. Compressed sensing (CS) has ushered in a new paradigm of undersampling data below the Nyquist rate to reduce acquisition time. An additional dimension of improvement using CS is to optimize the sampling pattern (SP) used to acquire undersampled data. The goal of the study was to apply learning based SP optimization for accelerating 3D-T_1ρ imaging of the brain.

Methods

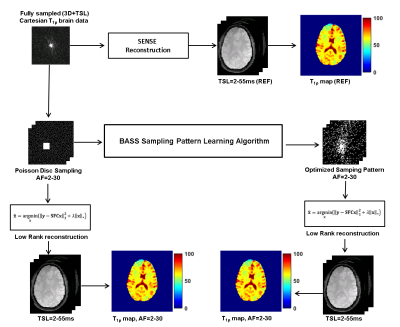
Five healthy volunteers (2 male/3 females, age = 28.8 ± 5.8 years) were recruited for the study. Fully sampled (FS) 3D-Cartesian T_1ρ weighted brain images were acquired on a clinical 3T MRI scanner with a vendor supplied 20 channel receive only head coil. The MR acquisition parameters included: TR = 5 ms, TE = 2.9 ms, T₁ delay = 1s, FOV = 240x240 mm², matrix size = 256x128x64, flip angle = 8°, slice thickness = 2 mm, spin-lock frequency = 500 Hz, spin lock (TSL) durations of 2, 4, 6, 8, 10, 15, 25, 35, 45, 55 ms, total acquisition time = 32 minutes.

Figure 1 shows a schematic representation of the data processing pipeline. FS Cartesian multi-coil data was reconstructed using sensitivity encoding (SENSE) reconstruction, and served as the reference(2). Poisson-disc (PD) sampling was used as the initial undersampling pattern, for acceleration factors (AF) of 2, 4, 6, 8, 10, 15, 20, 25, and 30. The new SP was optimized using a new machine learning algorithm, the bias accelerated subset selection (BASS) algorithm (3). The optimized SP was tested on separate training (5 images) and validation (5 images) data.

The optimal SP is given by:
$$\hat{Ω} = \arg\min_{Ω} \sum_{i=1}^{N_i} f( \mathbf{m}_{i} , FC R(S_Ω \mathbf{m}_{i}, Ω)) $$

and the efficiency of the SP was defined as:
$$f(\mathbf{m}_{i},\hat{\mathbf{m}}_{i})= \frac{|| \mathbf{m}_{i}- \hat{\mathbf{m}}_{i} ||_2^2}{|| \mathbf{m}_{i}||_2^2 } $$

where $$$\hat{Ω}$$$ is the estimated optimal SP of size M, $$$N_i$$$ is the number of data items used for training, $$$\mathbf{m}_{i}$$$ are the k-space data samples used for reconstruction, $$$ R(S_Ω \mathbf{m}_{i}, Ω) $$$ represents the fixed recovery algorithm used.

To test the efficacy of the optimized SP, all methods use the same low-rank reconstruction technique that used a nuclear norm of the reconstructed image vector x reordered as a Casorati matrix(4) and the cost-function was minimized using MFISTA-VA algorithm (5). Mono-exponential T_1ρ fitting of the reconstructed TSL time series was performed (6). Normalized root mean square error (NRMSE) was calculated optimized k-space, reconstructed images, and the NRMSE errors compared to the reference for the final T_1ρ maps.

Results

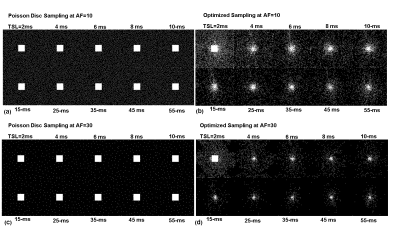
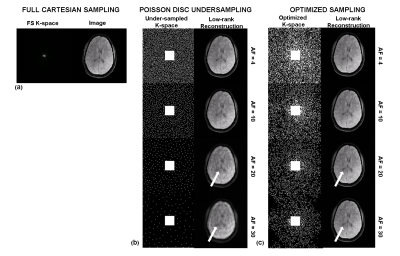
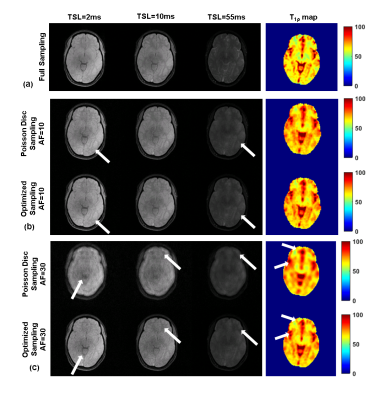
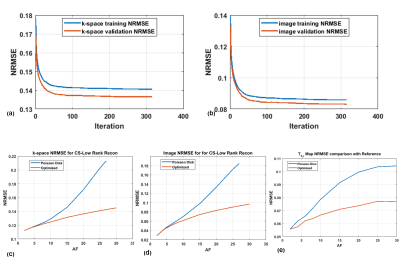
Figure 2 shows the initial PD sampling across the 2D+TSL time data and the optimized SP generated at different AFs. Figure 3 shows the comparison of performance between FS, PD and the optimized SP at increasing AFs. Figure 4 shows the performance difference between FS, PD and optimized SP for different TSL images, and the resulting T_1ρ map. Figure 5 shows the NRMSE errors for training and validation data, PD sampling and optimized SP at different AFs, and the resulting improvement of the optimized SP on the final brain T_1ρ maps at different AFs.

Discussion and Conclusion

The results in this study suggest optimized sampling improves significantly in performance with increased AF’s. Optimization of the SP is a potentially viable technique to reduce acquisition time using prospectively undersampled T_1ρ mapping sequences in the brain.

Acknowledgements

This research was supported by the This study is supported by NIH grants R21-AR075259-01A1, R01-AR076328, R01-AR067156, and R01-AR068966, and was performed under the rubric of the Center of Advanced Imaging Innovation and Research (CAI2R), an NIBIB Biomedical Technology Resource Center (NIH P41-EB017183).