1245
Accelerated MR parametric mapping with a hybrid deep learning model1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2Shenzhen College of Advanced Technology, University of Chinese Academy of Sciences, Shenzhen, China
Synopsis
Magnetic Resonance (MR) parametric mapping like $$$T_1$$$ , $$$T_2$$$, proton density is a powerful tool for biology tissue characterization, which is useful for clinical application such as diagnosis of pathologies including Alzheimer’s disease and multiple sclerosis1, evaluation of myocardial fibrosis2 and assessment of knee cartilage damage3. However the long scan time makes it challenging for practical clinical application. The purpose of this study was to develop a deep learning based method for accelerated MR parametric mapping with good performance at high acceleration rate both by reducing the contrast number and undersampling the k-space data.
Introduction
Quantitative Magnetic Resonance (MR) parametric mapping, such as $$$T_1$$$ , $$$T_2$$$, and, $$$T_{1\rho}$$$ 4-6 relaxations, is a powerful tool for assessing tissue properties in diagnosis and prognosis of diseases. However, parametric mapping requires the acquisition of multiply images with different contrast-weightings7, leading to long scan time that great hinders its wide clinical use. The total scan time is the scan time for a single-contrast image multiplying the contrast number in parametric direction. Intuitively, there are mainly two ways to reduce the scan time of parametric mapping: one is undersampling the k-space data of each image and the other is decreasing the contrast number. The prevailing methods for fast MR parametric mapping belong to the first one. They undersample the k-space data first, and then reconstruct the weighted images or the parametric maps using compressed sensing (CS) based algorithms8. Although these methods well explore the correlation between multi-contrast images, the achievable acceleration factor is still limited9. Therefore, it is expected that an acceleration method combined with under-sampling k-space data and decreasing the contrast number can yield good performance at high acceleration rate.Methods
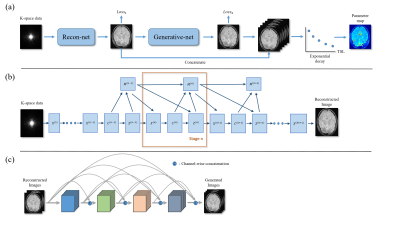
In this study, we propose a strategy to generate the synthetic multi-contrast images from the acquired images, reducing the scan time while keeping the contrast number. The integrated workflow of our method is shown in Fig.1. Our method is combined with a reconstruction module and a generative module. The reconstruction module can accelerate data acquisition with under-sampled k-space data. The generative module can generate some weighted images from two weighted input images with the constrains of similarity between historical multi-contrast images and the process of signal relaxation. The reconstruction module is based on Deep ADMM-Net10 . We take the fully sampled images as the ground truth $$$x^{gt}$$$, and under-sampled k-space data $$$y$$$ as the input. Then we constructed a training data set containing $$$L$$$ pairs of under-sampled k-space data and ground-truth image. We choose normalized mean square error (NMSE) as the loss function of reconstruction module:$$Loss_1=\frac{1}{L}\sum_{i=1}^{L}\frac{\sqrt{\lVert R(y_i|\theta)-x_i^{gt}\rVert_2^2}}{\sqrt{\lVert x_i^{gt} \rVert_2^2}} \tag{1}$$ Where $$$R(y_i|\theta)$$$ is the network output conditioned on network parameter $$$\theta$$$ and under-sampled k-space data $$$y_i$$$. We propose a supervised generative module with a densely connected convolution neural network structure to mapping the un-acquired weighted images directly to the fully sampled acquired images under the constraints of prior knowledge. The loss function can be described as: $$Loss_2=\frac{1}{L}\sum_{i=1}^{L} \lVert G(x_i|\theta-y_i)\rVert_2 \tag{2}$$Here $$$G(x_i|\theta-y_i)$$$ is the result of generated images with network parameter and input data $$$x_i$$$. $$$y_i$$$ represent the ground truth. $$$x_i$$$ is a two channel input stacked by No. 1 and 5 weighted images reconstructed by reconstruction module and $$$y_i$$$ is a three channel label data consists of the corresponding fully sampled No. 2, 3 and 4 weighted images. $$$L$$$ is the number of image pairs belong to a data set. As in most deep learning based image translation works, the $$$l_2$$$ norm is typically selected as a loss function to ensure the uniformity between the output images and ground truth.Results
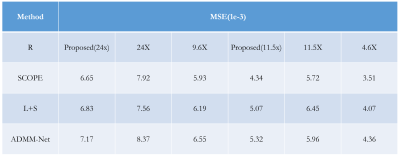
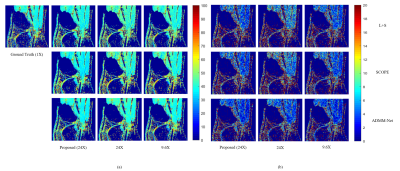
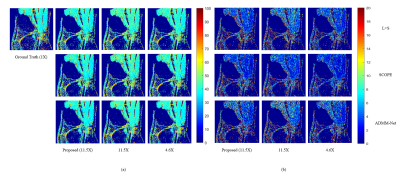
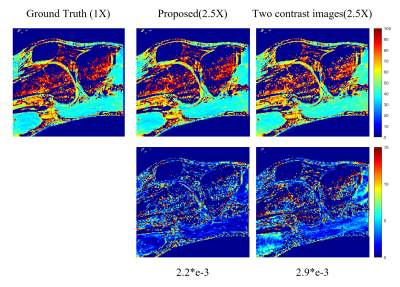
The experiments were conducted on a series of knee $$$T_{1\rho}$$$ weighted images with a in-plane resolution of 146 x 124 acquired on a 3T Siemens scanner at five different TSLs : 5, 10, 20, 40, 60 ms. These images are regarded as ground truth. There are total 512 slice images from two volunteers, among which 256 slices from one volunteer are used as training dataset and the rest images from another volunteer are used as testing dataset. The fully sampled k-space data was retrospectively under-sampled by Poisson variety density mask with R = 4.6 and 9.6 respectively to obtain the under-sampled k-space data. The generative module was also used as a plug in and play module for other reconstruction methods like SCOPE6 and L+S11. The $$$T_{1\rho}$$$ maps were evaluated using Mean Square Error (MSE) and ROI analysis. The evaluation was presented in Fig. 2 and ROI analysis was shown in Fig. 3, Fig. 4 and Fig. 5. The proposed method achieved better performance than k-space accelerated methods at different acceleration rate (Equivalent R = 24, 11.5 and 2.5 respectively) with evaluation based on both MSE and visual effect. With the proposed method, we can promote acceleration rate while not significantly reducing quality of parameters map.Conclusion and Discussion
In this work, an acceleration method for MR parametric mapping at high acceleration rate was developed, including a reconstruction module and a generative module. Our method is the first reported research to accelerate MR parameter mapping by combining reducing number of multi-contrast images to be acquired and under-sampling k-space data to the best of our knowledge. Moreover, the generative module also can be a plug in and play module in other reconstruction methods for better performance at high acceleration rate. In conclusion, the proposed method achieved better performance than other reconstruction methods at high acceleration rate, which may promote the practical clinical application of MR parameter mapping.Acknowledgements
This work is supported in part by the National Natural Science Foundation of China under grant nos. 61771463,81971611, National Key R&D Program of China nos. 2020YFA0712202, 2017YFC0108802 , the Innovation and Technology Commission of the government of Hong Kong SAR under grant no. MRP/001/18X, and the Chinese Academy of Sciences program under grant no. 2020GZL006.References
1. Bartzokis G, Sultzer D, Cummings J, et al. In Vivo Evaluation of Brain Iron in Alzheimer Disease Using Magnetic Resonance Imaging. Arch Gen Psychiatry. 2000;57(1):47–53.
2. Larsson HBW, Frederiksen J, et al. Assessment of demyelination, edema, and gliosis byin vivo determination of T1 and T2 in the brain of patients with acute attack of multiple sclerosis. Magn Reson Med. 1989;11(3):37–48.
3. Kim KA, Park MS, Kim IS, Kiefer B, et al. Quantitative evaluation of liver cirrhosis using T1 relaxation time with 3 tesla MRI before and after oxygen inhalation. J Magn Reson Imaging. 2012;36(40):5–10.
4. Shah NJ, Neeb H, Zaitsev M, et al. Quantitative T1 mapping of hepatic encephalopathy using magnetic resonance imaging. Hepatology. 2003;38:1219-1226.
5. Cieszanowski A, Szeszkowski W, Golebiowski M, et al. Discrimination of benign from malignant hepatic lesions based on their T2-relaxation times calculated from moderately T2-weighted turbo SE sequence. Eur Radiol. 2002;12:2273-2279.
6. Zhu Y, Liu Y, Ying L, et al. SCOPE: signal compensation for low-rank plus sparse matrix decomposition for fast parameter mapping. Phys Med Biol. 2018;63:185009.
7. les L, Pfluger H, Phrommintikul A, et al. Evaluation of diffuse myocardial fibrosis in heart failure with cardiac magnetic resonance contrast-enhanced T1 mapping. J Am Coll Cardiol. 2008;52:1574-1580.
8. Lee, D., Jin, et al. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA). Magn. Reson. Med.2016;76: 1848-1864.
9. Mandava, S, Keerthivasan, MB, et al. Accelerated MR parameter mapping with a union of local subspaces constraint. Magn. Reson. Med. 2018;80:2744– 2758.
10. Yan Yang, Jian Sun, Huibin Li, et al. Deep ADMM-Net for compressive sensing MRI. In Proceedings of the 30th International Conference on Neural Information Processing Systems. 2016;10–18.
11. Otazo, R., Candes E, Sodickson, et al. Low‐rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn. Reson. Med.2014;73: 1125-1136.
Figures