Introduction

NAD⁺ and NADH play important roles as electron acceptor and donor respectively and high concentrations of NAD⁺ and a high ratio of NAD⁺/NADH are both strongly associated with metabolic health [1]. This makes the non-invasive quantification of these metabolites very interesting for metabolic research. On 3T clinical scanners however, there is severe overlap between α-ATP and NAD⁺/H resonances in ³¹P spectra [2]. Therefore, spectral editing of α-ATP is a promising way to visualize and quantify the underlying NAD⁺/H resonances. We used the principle of the Bilinear Rotation Decoupling (BIRD) filter [3] to suppress homonuclear coupled spins, such as α-ATP, based on their J-coupling constant. This new sequence was validated in vivo by measuring the NAD⁺/H levels in the lower legs of eight volunteers in basal state and during ischemia, as it is well known that ischemia increases NADH and decreases NAD+ concentrations [4].

Methods

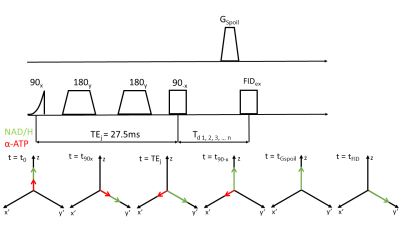
Eight young and healthy volunteers were positioned in the scanner (Achieva 3T, Philips Health Care, Best, the Netherlands) with an inflatable cuff around their upper leg. A 10cm single tuned ³¹P surface coil (Philips Health Care, Best, the Netherlands) was used to acquire FIDs in the lower leg in rest (deflated cuff) with NSA=32, points=2048, BW=3000Hz and TR=4000ms. Subsequently, homonuclear BIRD (HB) filtered spectra were acquired in rest and during eight minutes of ischemia created by inflating the cuff to a pressure of 50mmHG above systolic blood pressure. At TE=1/2J, α-ATP spins acquire a phase of 90⁰ with respect to uncoupled spins at in spin echo sequences [5] and we can see the spins as a rotated coordinate system where the z-axis is unchanged, uncoupled spins are create the axis x’ and coupled spins create the axis y’. Flipping spins about the y’-axis by -90⁰ results in uncoupled spins ending up aligned with the z-axis, whereas α-ATP spins remain in the x’-y’ plane and are dephased by a spoiler-gradient. A subsequent excitation only affects spins, which are aligned with z. Zero quantum coherences (ZQC) are removed by co-adding signals acquired with a variable delay T_d between HB filter and FID excitation [6]. A depiction of the sequence is displayed in Figure 1. Scan parameters were as follows: NSA=128, points=2048, BW=3000Hz, TR=4000ms, TE_j=27.5ms, T_d=n/(-f_βATP-f_αATP) with n=1…32. In order to judge whether the HB filter is really necessary, we also aimed to determine NAD⁺/H levels from a simple FID. Spectra were analysed with the help of an in-house developed MATLAB script (MATLAB 2018b, The MathWorks,Inc.). The program first fitted resting state spectra and used the resulting fit parameters as starting values for fitting spectra acquired during ischemia. A Monte-Carlo simulation was performed for all data sets to determine Cramer-Rao lower bounds. Reproducibility of the HB filter sequence was tested by performing repeated in vivo measures (N=2) and comparison of their respective fitting results.

Results

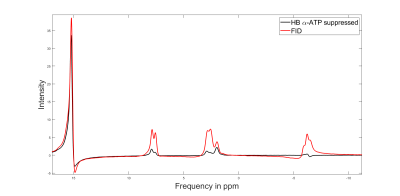
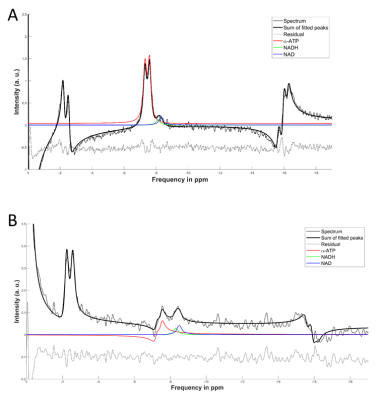
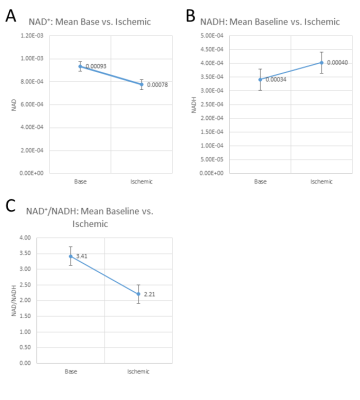
Figure 2 shows a comparison between FID and HB filtered spectra acquired from an ATP+NAD⁺ phantom. The HB filter thereby succeeded in suppressing α-ATP by 85%. Signal loss of NAD⁺/H between FID and HB filter spectra was ~30%. Reproducibility tests showed a coefficient of variation of 6.4% for NAD⁺ values, 10.8% for the sum of NAD⁺ and NADH, 36.9% for NADH. Ratios of NAD⁺/NADH varied by 62.8%. Results from Monte-Carlo simulations show an average relative Cramer-Rao lower bound of 25.3% for NADH and 11.1% for NAD⁺. Figure 4 shows results of resting state vs. ischemic spectra. NAD⁺ decreased significantly in ischemia (p<0.05), NAD⁺/NADH tended to decrease, while the increase in NADH was not significant (p=0.21). When quantified in a simple FID, the NAD⁺ and NADH signal intensities varied over a wide range with a prominent remaining residual in NAD⁺/H peak fits of the FID (Figure 3A), which is minimized in the edited spectrum. In addition, a clear separation of α-ATP is visible in the edited spectra compared to an FID (Figure 3B).

Discussion

The homonuclear BIRD filter successfully suppresses a-ATP and uncovers NAD⁺/H resonances. This novel approach allows the observation of expected changes in NAD⁺ concentrations upon ischemia. However, the separation of NADH and NAD⁺ remains challenging and requires a fitting procedure with strong prior knowledge. As the NADH concentrations are generally lower than the NAD⁺ concentrations, the relative error was higher for the determination of NADH than for NAD⁺. From the results of the reproducibility, we can see that while reproducibility of NAD⁺ and the sum of NADH+NAD⁺ is good, the NADH quantification remains challenging. The variability in NADH also explains the variability of NAD⁺/NADH ratios. Residual α-ATP may result from suboptimal TE_j, as the assumption of J_αATP=18Hz [7] was probably not exactly correct as actual in vivo J-coupling constants of α-ATP appear to lie between 12 and 15Hz. To improve the performance of the HB filter further, an adjustment of TEj to match the in vivo J-coupling constants could be tested.

Conclusion

The HB filter is a feasible approach for the detection of NAD⁺ and for the sum of NADH and NAD⁺. Further improvements such as optimizing TEj to reach a better α-ATP suppression might improve the accuracy of NAD⁺/NADH ratio quantification.

Acknowledgements

No acknowledgement found.