1214

Consolidated simulation of ²³Na Dynamics in Biological Tissue

Chengchuan Wu¹, Yasmin Blunck¹, and Leigh A. Johnston¹
¹Department of Biomedical Engineering, The University of Melbourne, Parkville, Australia

Synopsis

This work presents a mathematical framework that enables the simulation for the dynamics of the spin-3/2 ²³Na density operator. The simulator is featured with easy implementation for ²³Na in biological environment. This work demonstrates the simulator in two ²³Na pulse sequences.

Introduction

The sodium nucleus is a sensitive biomarker of tissue viability and organ function abnormality¹. Imaging sequences that probe apects of sodium MR behaviour require simulation, however the spin-3/2 ²³Na experiences quadrupolar interactions and exhibits complex evolution where non-zero average electric field gradients (EFG) are present, making simulation challenging. The spin-1/2 Bloch equation (BE) has been used as a first-order approximation^2,3. Despite the ease of implementation, BE neglects multiple-quantum coherences that produce bi-exponential decay and multiple-quantum filtered signals. Simulations with sufficient coherence terms have been proposed^4-6, however under assumptions that applied in specific conditions.

In this work, we encapsulate all necessary components of ²³Na dynamics for simulation into a single generalised equation, herein referred as the ‘Sodium Bloch Equation’ (SBE), in analogy with the matrix-vector form of the BE. Our derivation is based on irreducible spherical tensor operator (ISTO) formalism^4,5(https://github.com/chengchuanw/Sodium_spin_dynamics_simulation). Where previously ²³Na-MRI simulation was a piecewise process, the SBE requires definition of one 15x15 system matrix and the initial condition vector. We detail the SBE and demonstrate its utility via simulation of two ²³Na pulse sequences, comparing results with the spin-1/2 BE.

Methods

SBE: the SBE can be written in the matrix-vector form akin to the BE, as
$$\frac{d}{d t}\mathbf{P} = \mathbf{L}\mathbf{P} + \mathbf{C}.
$$Here, $$$\mathbf{P}$$$ is ISTO basis defined as in the literature⁴:
$$ \{\hat{T}_{l0}, \hat{T}_{lm}(a), \hat{T}_{lm}(s)\,|\, l = 0,1,2,3,\, m = 1,\dots,l \}.$$
Under this definition, the $$$\hat{T}_{11}(a)$$$, $$$\hat{T}_{11}(s)$$$ and $$$\hat{T}_{10}$$$ are proportional to the x-, y- and z-magnetisation, respectively⁴.
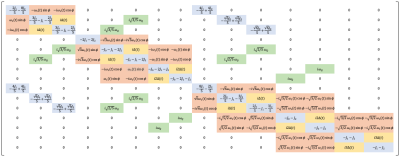
$$$\mathbf{L}$$$ is the system matrix detailed in Fig. 1. The matrix $$$\mathbf{L}$$$ is parameterised by RF amplitude, $$$ \omega_1(t)$$$, the initial RF phase, $$$\phi_0$$$ with reference to the x′-axis, off-resonance frequency, $$$\omega_\Delta(t)$$$, residual quadrupolar frequency, $$$\omega_Q$$$, and spectral densities, $$$J_0$$$, $$$J_1$$$ and $$$J_2$$$.
$$$\mathbf{C}$$$ is the offset given as
$$\mathbf{C} = [\frac{2}{5}J_1+\frac{8}{5}J_2,0,0,0,0,0,0,0,\frac{4}{5}J_1-\frac{4}{5}J_2,0,0,0,0,0,0]^\top,$$
where the thermal equilibrium, $$$\mathbf{P}(0) = \hat{T}_{10}$$$ is defined.

Bloch Equation simulations: For comparison with the SBE, the BE simulations assume that ²³Na magnetisation experiences mono-exponential relaxation with $$$T_1$$$ and $$$T_2$$$.

Simulated motion regime⁷:
Saline (isotropic, fast-motion regime): $$$J_0$$$=$$$J_1$$$=$$$J_2$$$=8.9 Hz, $$$\omega_Q$$$= 0 Hz. $$$T_1$$$ = 56.7 ms, $$$T_2$$$ = 56 ms;
3% xanthan gel (anisotropic, slow-motion regime): $$$J_0$$$=319 Hz, $$$J_1$$$=28.2 Hz, $$$J_2$$$=28.1 Hz, $$$\omega_Q$$$=61.8 Hz. $$$T_1$$$ = 17.3 ms, $$$T_2$$$ = 3.7 ms.

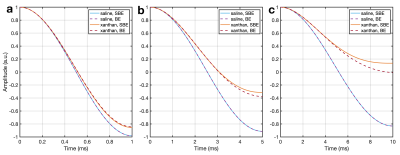
Rectangular Inversion pulse simulation: ²³Na spin evolution was simulated during an on-resonance inversion pulse⁸, for pulse durations 1 ms, 5 ms and 10 ms. Numerical integration was used to solve the SBE and BE in MATLAB using ode45.

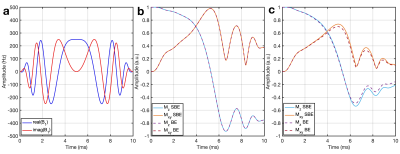
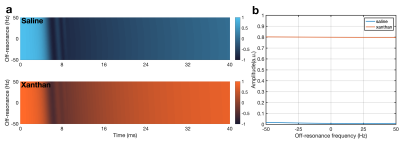
WURST simulation: ²³Na spin evolution during the adiabatic Wide-band Uniform Rate and Smooth Truncation (WURST) IR sequence² was simulated, following Madelin et. al.² across off-resonance ranging -50-50 Hz.

Results

Rectangular Inversion pulse: Fig. 2 shows the evolution of the longitudinal magnetisation during pulses of various durations. The SBE results agree well with the literature⁸. The comparison between the SBE and BE demonstrates negligible difference for saline, as expected. For xanthan, differences are noted between the two approaches, which increase with the duration of the pulse, reinforcing the importance of simulating complete sodium dynamics.

WURST: The pulse shape and the magnetisation evolution are shown in Fig. 3. Similar to the rectangular pulse, differences were observed between SBE and BE in xanthan. Fig. 4(a) depicts the longitudinal magnetisation evolution during the preparatory phase, in the presence of off-resonances. The prepared longitudinal magnetisation amplitude at the instant before the excitation pulse is shown in Fig. 4(b), demonstrating the strength of the SBE simulator in revealing the sequence’s robustness to $$$B_0$$$ inhomogeneity.

Discussion

The SBE is a generalised model for ²³Na spin dynamics that arises from a consolidation of existing equations in the literature^4,5. The SBE formalism holds under the simple assumption that correlation times are sufficiently short, a condition met in biomedical tissue imaging environments (e.g. Shekar et. al.⁹). With the SBE, there is no need for a piecewise treatment to analyse a sequence; simulation is trivial, requiring only a one-line call to an ode solver based on a single 15x15 system matrix, which takes only a few seconds on a standard laptop. The SBE simulator works in the tensor operator basis. with the computational cost lower than the NMR package, SpinDynamica, which operates in the underpinned Zeeman basis.

We verified the behaviour of the SBE through simulations, demonstrating the expected negligible difference between SBE and BE for fluid regions. Literature suggests that the BE will be erroneous in tissue with extreme parameters such as cartilage³. Having outlined the computational framework, it is now straight-forward for ²³Na imaging sequences to be simulated and understood.

Conclusion

The SBE offers a general representation of ²³Na spin dynamics in biological tissue imaging environments, encapsulated in a single 15x15 system matrix, akin to the 3x3 Bloch equation matrix for spin-1/2 nuclei. The SBE is straight-forward to implement, defining only one matrix and initial condition vector, and requiring one call to an ode solver, greatly improving the accessibility of sodium MRI simulations and sequence design and development.

Acknowledgements

We acknowledge the facilities, and the scientific and technical assistance of the Australian National Imaging Facility, a National Collaborative Research Infrastructure Strategy (NCRIS) capability, at the Melbourne Brain Centre Imaging Unit of the University of Melbourne. The work was also supported by a research collaboration agreement with Siemens Healthineers.

References

[1] G. Madelin, R. Kline, R. Walvick, R. R. Regatte, A method for estimating intracellular sodium concentrationand extracellular volume fraction in brain in vivo using sodium magnetic resonance imaging, Scientific Reports4 (2014) 4763

[2] G. Madelin, J.-S. Lee, S. Inati, A. Jerschow, R. R. Regatte, Sodium inversion recovery MRI of the knee jointin vivo at 7T, Journal of Magnetic Resonance 207 (1) (2010) 42–52.

[3] F. J. Kratzer, S. Flassbeck, A. M. Nagel, N. G. Behl, B. R. Knowles, P. Bachert, M. E. Ladd, S. Schmitter,Sodium relaxometry using 23Na MR fingerprinting: A proof of concept, Magnetic Resonance in Medicine 84 (5)(2020) 2577–2591.

[4] J. R. van der Maarel, Thermal relaxation and coherence dynamics of spin 3/2. I. Static and fluctuatingquadrupolar interactions in the multipole basis, Concepts in Magnetic Resonance 19A (2) (2003) 97–116.

[5] J. R. van der Maarel, Thermal relaxation and coherence dynamics of spin 3/2. II. Strong radio-frequency field,Concepts in Magnetic Resonance 19A (2) (2003) 117–133. doi:10.1002/cmr.a.10088.

[6] C. Tanase, F. E. Boada, Algebraic description of spin 3/2 dynamics in nmr experiments, Journal of MagneticResonance 173 (2) (2005) 236–253.

[7] T. Wilferth, L. V. Gast, R. W. Stobbe, C. Beaulieu, B. Hensel, M. Uder, A. M. Nagel, 23Na MRI of human skeletal muscle using long inversion recovery pulses, Magnetic Resonance Imaging 63 (2019) 280–290.

[8] R. Stobbe, C. Beaulieu, In vivo sodium magnetic resonance imaging of the human brain using soft inversionrecovery fluid attenuation, Magnetic Resonance in Medicine 54 (5) (2005) 1305–1310.

[9] Shekar, S. C., Tang, J. A., & Jerschow, A. Dynamics of I=3\over2 nuclei in isotropic slow motion, anisotropic and partially ordered phases. Concepts in Magnetic Resonance Part A. (2010), 36(6), 362-387.

Figures

Figure 1: The SBE system matrix, $$$\mathbf{L}$$$, colour-coded to indicate source of terms: Red-shaded entries are associated with RF excitation; Yellow-shaded entries are off-resonance terms; Green-shaded terms are associated with residual quadrupolar oscillation; Blue-shaded terms are associated with the fluctuating quadrupolar interaction.

Figure 2: The simulation for rectangular IR pulse. Evolution of the longitudinal magnetisation under inversion pulses with duration of (a) 1 ms; (b) 5 ms; (c) 10 ms are shown.

Figure 3: (a) Shape of the WURST inversion pulse, and the evolution of bulk magnetisation in (b) saline, (c) xanthan.

Figure 4: SBE simulation depicting (a) the amplitude of the longitudinal magnetisation during the preparatory stage of the WURST IR pulse with the influence of $B_0$ inhomogeneity, and (b) their values instantaneously before the excitation pulse, which indicate that the sequence is $$$B_0$$$ insensitive.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1214