1189
Improved CS-MRI using Hybrid Plug-and-Play Priors based Fast Composite Splitting Algorithm
Qingyong Zhu1, Jing Cheng2, Zhuo-Xu Cui1, and Dong Liang1,2
1Research Center for Medical AI, SIAT, Chinese Academy of Sciences, Shenzhen, China, 2Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, Chinese Academy of Sciences, Shenzhen, China
1Research Center for Medical AI, SIAT, Chinese Academy of Sciences, Shenzhen, China, 2Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, Chinese Academy of Sciences, Shenzhen, China
Synopsis
The Plug-and-Play prior (PnP) is also known as denoising prior which has been successfully utilized in non-linear imaging problems. The paper presents a hybrid PnP which is incorporated into the fast composite splitting algorithm (FCSA) for compressed sensing magnetic resonance imaging (CS-MRI). The advantage of the hybrid PnP over generic PnP such as BM3D is that it can further remove artifacts and preserve adaptively fine structures in CS-MRI reconstruction. Experimental results and performance comparisons with generic PnP-FISTA show the superiority of the proposed approach even for high acceleration factor.
Introduction
In compressed sensing $$$^{1,2,3}$$$ based magnetic resonance imaging (CS-MRI), the k-space measurement takes the form: $$y=F_{u}x+n~~~~~~~~~~(1)$$where $$$F_{u}\in \mathbb{C}^{m\times n}$$$ is the under-sampled Fourier encoding matrix. $$$n$$$ is observed noise supposed to be complex Gaussian. The problem of recovering the desired image $$$x\in\mathbb{C}^{n\times1}$$$ from the compressed measurement $$$y\in\mathbb{C}^{m\times1}$$$ is usually solved by minimizing a cost function:$$\min_{x}\parallel F_{u}x-y\parallel_{2}^{2}+\lambda \mathcal{R}(x)~~~~~~(2)$$where $$$\mathcal{R}(x)$$$ is the regularization term (e.g., total variation$$$^{4}$$$). The positive weight $$$\lambda$$$ controls the trade-off between the data fitting and the regularity. Plug-and-play prior based fast iterative shrinkage/thresholding algorithm (PnP-FISTA)$$$^{5}$$$ has been used for solving (2) and it can be summarized as follows:$$z^{t}\leftarrow x^{t-1}+\tau F_{u}^{H}(y-F_{u}s^{t-1});\\x^{t}\leftarrow \mathcal{D}(z^{t},\sigma);\\q_{t}\leftarrow(1+\sqrt{1+4q_{t-1}^{2}})/2;\\s^{t-1} \leftarrow x^{t}+(\frac{q_{t-1}-1}{q_{t}})(x^{t}-x^{t-1})$$where $$$q_{0}=1$$$, $$$x^{0}=s^{0}=F_{u}^{H}y$$$. $$$F_{u}^{H}$$$ is the adjoint operator for $$$F_{u}$$$. $$$x^{t}$$$ is the reconstructed image at $$$t$$$-th iteration. $$$\tau$$$ is a step-size. The operator $$$\mathcal{D}$$$ is usually a general denoiser with strength $$$\sigma$$$. However, the denoiser is chosen traditionally as data-independent, failing to clear out artifacts and meanwhile preserve adaptively edge information. Here we propose a hybrid PnP based fast composite splitting algorithm (FCSA), named as HPnP-FCSA, which integrates the internal PnP using Block Matching and 3D filtering (BM3D)$$$^{6}$$$ on the target image only and external PnP using mutually guided image filtering (muGIF) $$$^{7}$$$ based on reference image to further develop the morphology information of the target image. A high spatial-resolution reference image can be easily obtained by a pre-scan in various MR applications and provides rich structure priors to help improve imaging quality $$$^{8,9}$$$. Experimental comparisons with generic PnP-FISTA show the superiority of the proposed approach.Method
The FCSA was implemented by combining FISTA$$$^{10}$$$ and composite splitting denoising (CSD)$$$^{11}$$$. The CSD can split the reconstruction model into multiple sub-problems and then combines the sub-solutions linearly to obtain the final result. Besides, FCSA inherits the fast convergence and effective reconstruction of FISTA and thus can effectively solve the model (2). The proposed HPnP-FCSA for CS-MRI reconstruction can be summarized as follow: $$z^{t}\leftarrow x^{t-1}+\tau F_{u}^{H}(y-F_{u}s^{t-1});\\x^{t}_{BM3D}\leftarrow \mathcal{D}_{BM3D}(z^{t},\sigma);\\x^{t}_{muGIF}\leftarrow \mathcal{D}_{muGIF}(z^{t},x_{r},\eta);\\x^{t}\leftarrow \alpha x^{t}_{BM3D}+(1-\alpha)x^{t}_{muGIF};\\q_{t}\leftarrow(1+\sqrt{1+4q_{t-1}^{2}})/2;\\s^{t-1} \leftarrow x^{t}+(\frac{q_{t-1}-1}{q_{t}})(x^{t}-x^{t-1})$$ where $$$\mathcal{D}_{BM3D}(z^{t},\sigma)$$$ and $$$\mathcal{D}_{muGIF}(z^{t},x_{r},\eta)$$$ represents the internal PnP and external PnP, respectively. $$$\sigma$$$ and $$$\eta$$$ are the corresponding denoising-strength parameters. $$$x_{r}$$$ is a fully-sampled reference image. $$$\alpha\in(0,1)$$$ is weighting constant. In internal PnP, the BM3D is a denoising technique from the non-local means class that groups similar shapes and puts into a 3D array. Efficient collaborative filtering is performed by thresholding in 3D transform domain. In external PnP, the muGIF is an extended version of guided image filtering (GIF) $$$^{12}$$$ and aims to enhance the capability of filtering process in restoring structure of the target image based on mutual structure that is contained in both target and reference images. The mutual structure is defined as follow:$$\mathcal{MS}(x,x_{r}) = \sum_{i}\sum_{j\in\left\lbrace h,v\right\rbrace}\frac{|\triangledown_{j}x_{i}|}{|\triangledown_{j}x_{r,i}|}+\sum_{i}\sum_{j\in\left\lbrace h,v\right\rbrace}\frac{|\triangledown_{j}x_{r,i}|}{|\triangledown_{j}x_{i}|}$$ where $$$\triangledown$$$ is the first order derivative filter containing horizontal and vertical directions. For more details of optimization, please refer to the work$$$^{7}$$$.Experiment
The experiments are carried out on in-vivo $$$T2$$$-weighted brain MR images including multiple flip-angle images. 1D variable density random under-sampling pattern is adopted to generate sampled k-space data. The PnP-FISTAs with two different denoisers are compared. In addition, the step-size $$$\tau$$$ is fixed as 1. The weight $$$\alpha$$$ is fixed as 0.5. All algorithms were run for 250 iterations. All reconstructions were performed in Matlab R2017a on a standard laptop (Windows 10, 64 bit operation system, Intel(R) Core(TM) i7-9700 CPU, 3 GHz, 32 GB RAMS). The reconstruction quality is quantified with the relative error (RE) and peak signal to noise ratio (PSNR), which are defined as RE$$$(\%)={\parallel x-\hat{x}\parallel_{2}}/{\parallel x\parallel_{2}}\times 100\%$$$, PSNR (dB)$$$=20{\textrm{log}}_{10}(max(x)\sqrt{n}/{\parallel x-\hat{x}\parallel_{2}})$$$, where $$$x$$$ and $$$\hat{x}$$$ denote the fully-sampled original image and the reconstructed image, respectively.Results
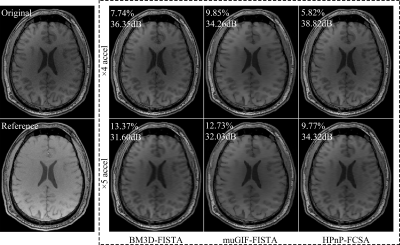
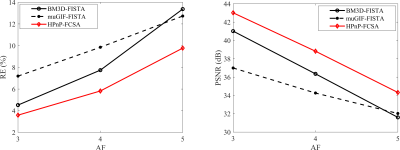
The experimental results are shown in Figure 1. The returned image of BM3D-FISTA is sharpened but still has unacceptable distortion. The muGIF-FISTA provides a promising results that the aliasing artifacts are significantly suppressed and more details are efficiently preserved. However, some fine structures still suffer from over-smoothing. As expected, the HPnP-FCSA further defines meaningful details and shows the best reconstruction-ability. Furthermore, the corresponding RE and PSNR plots of the reconstructed images using all methods at different acceleration factors (AF=3, 4, 5) are given in Figure 2. It can be easily noticed that the HPnP-FCSA returned the images that exhibit the lowest RE and highest PSNR values. Based on our experiments, the HPnP-FCSA can further help recover fine structures in CS-MRI.Conclusion
In this work, a novel HPnP-FCSA has been introduced for fast MRI reconstruction from under-sampled k-space data. Experimental results on in-vivo brain MR images have illustrated that the proposed HPnP-FCSA is effective.Acknowledgements
This work was supported in part by the National Key R&D Program of China (2017YFC0108802 and 2017YFC0112903); National Natural Science Foundation of China (61771463, 81830056, U1805261, 81971611, 61871373, 81729003, 81901736); Natural Science Foundation of Guangdong Province (2018A0303130132); Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province; Shenzhen Peacock Plan Team Program (KQTD20180413181834876); Innovation and Technology Commission of the government of Hong Kong SAR (MRP/001/18X); Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000).References
- Donoho D. Compressed sensing. IEEE Transactions on Information Theory. 2006; 52(4): 1289-1306.
- Candès E, Romberg J, Tao T. Robust uncertaintyprinciples: exact signal reconstruction from highly incomplete frequency information.IEEE Transactions on Information Theory. 2006; 52(2): 489-509.
- Chartrand R. Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Processing Letters. 2007; 14(10): 707–710.
- Lustig M, Donoho D, Pauly J. Sparse MRI: The applicationof compressed sensing for rapid mr imaging. Magnetic Resonance in Medicine. 2007; 58(6): 1182-1195.
- Kamilov U, Mansour H, Wohlberg B. A Plug-and-Play priors approach for solving nonlinear imaging inverse problems. IEEE Signal Processing Letters. 2017; 24(12): 1872-1876.
- Dabov K, Foi A, Katkovnik V, et al. 2007. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing. 2007; 16(8): 2080-2095.
- Li Y, Ma J Y, Guo X J, et al. Mutually Guided Image Filtering. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2020; 42(3): 694-707.
- Gong E, Huang F, Ying K, et al. 2015. PROMISE: parallel-imaging and compressed-sensing reconstruction of multicontrast imaging using sharable information. Magnetic Resonance in Medicine. 2015; 73(2):523–535.
- Zhu Q, Wang W. Improving multi-contrast imaging with reference guided location and orientation priors on edges. Applied Magnetic Resonance. 2019; 50(1-3):137-158.
- Teboulle M Beck A. A Fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences. 2009; 2(1):183-202.
- Huang J, Zhang S, Li H, et al. Composite splitting algorithms for convex optimization. Computer Vision & Image Understanding. 2011;115(12):1610-1622.
- He K, Sun J, Tang X. Guided image filtering. IEEETransactions on Pattern Analysis and Machine Intelligence. 2013; 35(6):1397-1409.