1185
Iterative Reconstruction for Enhanced Through-Plane Resolution T2-Weighted Spin-Echo Imaging of the Prostate
Eric A Borisch1, Roger C Grimm1, Soudabeh Kargar2, Akira Kawashima3, Joshua D Trzasko1, and Stephen J Riederer1
1Radiology, Mayo Clinic, Rochester, MN, United States, 2Radiology, University of Wisconsin-Madison, Madison, WI, United States, 3Radiology, Mayo Clinic, Phoenix, AZ, United States
1Radiology, Mayo Clinic, Rochester, MN, United States, 2Radiology, University of Wisconsin-Madison, Madison, WI, United States, 3Radiology, Mayo Clinic, Phoenix, AZ, United States
Synopsis
A previously described method for producing an image stack with enhanced through-plane resolution from an acquired set of overlapping thicker 2D slices is limited by noise enhancement when a linear reconstruction is used. To improve the resulting sharpness and noise performance of the output images, a sparsity-regularized (wavelet) full forward model based iterative reconstruction is developed. Initial results with a composite-splitting gradient descent solver provide promising noise and resolution enhancement performance. Future work includes refinements to the forward model and improving optimization convergence of the solver through momentum-based algorithms.
Introduction
A method for reconstructing thin (e.g. 1mm) T2-weighted spin-echo (T2SE) slices of the prostate from overlapping thick (e.g. 3mm, acquired on the finer grid) acquired slices by accounting for the slice profile (blur) during reconstruction has been previously demonstrated1 with a standard linear reconstruction. The “kZ-multislice” (KZM) reconstruction process involves recovering signal that has been suppressed by the slice profile, which in turn amplifies noise, an undesirable side effect. This work details progress on a full forward model, iterative, sparsity-enforcing reconstruction to improve the quality of the output images.Methods
Similar to described super-resolution techniques2, this acquisition and reconstruction seek to leverage the information contained in multiple data sampling events of the same object to recover resolution data beyond that of the explicitly performed acquisitions. To provide a more effective control of noise amplification during the reconstruction process (and thereby enable more aggressive resolution recovery), a model-based iterative reconstruction (MBIR) process has been developed. Explicitly, we model the three dimensional (pre-whitened)3,4 received signal y as: $$y=\Gamma F \Phi B C x + \epsilon = A x + \epsilon$$ where x is the object's signal intensity, C the coil responses, B the slice excitation profile (along z; convolutional with padding at edges), 𝛷 selects only the portion of the reconstructed volume encoded in y, F is the Fourier transform along x and y, and 𝛤 selects only those points sampled in k-space, while 𝜖 is additive white Gaussian noise. We seek to minimize the sparsity-regularized cost term: $$J(x) = \frac{\lambda}{\left|\Omega\right|}\sum\nolimits_{n\in\Omega}\left|\left|{\Psi \Delta_n}\right|\right|_1+\left|\left|{Ax-g}\right|\right|_2^2$$ where the sparsifying transform 𝛹 is here a lifted5 3D Daubechies-4 wavelet transform6 and $$$\Delta_n$$$ is a 3D spatial shifting or cycle-spinning operator, applied for a shift from set $$$\Omega$$$, which approximates shift-invariance for the wavelet transform7,8. This minimization is currently performed with composite splitting projected gradient descent9, which comprises the following iteration: $$x_{t+1} = \frac{1}{\left|\Omega\right|}\sum\nolimits_{n\in\Omega}\Delta_n^*\Psi^*S_{\lambda \tau /2}\left\{ \Psi\Delta_n(x_t - \tau A^*( Ax_t-g)) \right\}$$ where * denotes the Hermitian transpose operator, 𝜏 = 1 / max(eigenvalues(A*A)), and S is the soft thresholding operator: $$S_\gamma(x)=\begin{cases}x\frac{\left|x\right|-\gamma}{\left|x\right|}, & if \left|x\right| \ge \gamma\\0, & otherwise\end{cases}$$ The regularization parameter lambda (or thresholding parameter gamma where $$$\gamma=\lambda\tau/2$$$) is selected to balance sharpness and noise suppression.The coil response map C was extracted from the auto-calibration lines of the acquisition as described in ESPIRiT10, utilizing the central 24 × 24 region of the autocalibration signal, a 6 × 6 kernel size and an eigenvalue cut-off of 10-3, followed by (Gaussian) filtering performed after extraction to improve slice-to-slice consistency within the calibration maps (in keeping with the slow physical change in sensitivity along the slice direction for an axial acquisition with surface coils). The $$$\Delta_n$$$ operator set contained 24 (6 × 2 × 2 in slice, phase, and frequency) shifts. Six slice-shifts were used to match the number of acquisition passes, and was found to provide superior results compared to symmetric (eg. 3 × 3 × 3) neighborhoods.
The solver was implemented in MATLAB with compiled C++ code for the lifted wavelet transform, and was applied retrospectively to data acquired11 under an IRB-approved protocol on 14 male patients for whom prostate MRI was clinically indicated and performed separately. For each patient 78 3mm thick slices were acquired in 6:40 using TR 3000, TEEFF 10, ETL 21, and 0.75 × 0.75 mm2 inplane resolution and 16 coil elements. Results were evaluated radiologically to note any trends.
Results
Figure 1 shows axial T2SE images of the prostate of one subject: (A) standard 3mm thick T2SE (acquired in 4:14) and (B-F) 1mm thick images. (B) was reconstructed using the linear KZM method1, while (C-F) were generated with the new MBIR at the λ values shown. Note some improved sharpness of (B) vs. (A) owing to the thinner slice but an increased noise level. MBIR with increasing λ provides progressive reduction in noise in (C-F). However, use of λ=0.00075 caused undesirable blurring, e.g. between the peripheral and transition zones (F, arrow).Figure 2 shows results from a second case. Fig. 2B vs. A better portrays a lesion (B, arrow), but MBIR provides further improved depiction (D, yellow arrow) and definition of a second lesion (orange arrow). Higher λ values again cause blur. Across the patient studies the radiologist’s perceived preference was for λ=0.00025.
Discussion
As has been demonstrated12-14 elsewhere, sparsity-regularized MRI reconstructions can provide significant improvements over traditional (linear) reconstruction methods. Here a wavelet transform with shrinkage was used as the sparsity-enforcing operator, and yielded improved noise and sharpness performance while reconstructing the higher-resolution volume when compared to the linear reconstruction technique.Motion remains a concern with multi-pass acquisitions, and has not been directly addressed in this reconstruction, but may be added to the forward model in the future by including distortions detected via slice-to-slice correlations15.
Conclusion
An iterative, sparsity-regularized reconstruction has been demonstrated for a resolution-enhancing reconstruction of the prostate with potential improvement over linear reconstruction. Improving the reconstruction speed is critical for this to become clinically useful; future work will focus on improving optimization convergence through use of momentum-based algorithms like the Fast Composite Splitting Algorithm (FCSA)9 , which is the multi-penalty generalization of FISTA16.Acknowledgements
NIH RR018898
Mayo Clinic Discovery Translation Fund
References
- Kargar, S, et al. Use of kZ‐space for high through‐plane resolution in multislice MRI: Application to prostate. Magn Reson Med. 2019;81(6):3691– 3704.
- Greenspan, H, et al. MRI inter-slice reconstruction using super-resolution, Magnetic Resonance Imaging. 2002;20(5):437-446.
- Pruessmann, KP, et al. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med. 2006;42(5):952-962.
- Ramani S, et al. Parallel MR image reconstruction using augmented Lagrangian methods. IEEE Trans. Med. Imag. 2011;30(3):694-706.
- Sweldens, Wim. The lifting scheme: a construction of second generation wavelets. SIAM Journal on Mathematical Analysis. 1998;29(2):511–546.
- Daubechies, Ingrid. Ten Lectures on Wavelets, SIAM 1992.
- Figueiredo, MAT, et al. majorization–minimization algorithms for wavelet-based image restoration. IEEE Transactions on Image Processing. 2007;16(12):2980-2991.
- Guerquin-Kern, M, et al. A fast wavelet-based reconstruction method for magnetic resonance imaging. IEEE Trans. Med. Imag., 2011; 30(9):1649–1660.
- Huang, J, et al. Composite splitting algorithms for convex optimization. Computer Vision and Image Understanding. 2011;115(12):1610-1622.
- Uecker M, et al. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990-1001.
- Kargar, S, et al. Modified acquisition strategy for reduced motion artifact in super resolution FSE multislice MRI: application to prostate. Magn Reson Med. 2020;84(5):2537– 2550.
- Lustig, M, et al. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-95.
- Trzasko, JD, et al. Sparse-CAPR: highly accelerated 4D CE-MRA with parallel imaging and nonconvex compressive sensing. Magn Reson Med. 2011;66(4):1019-32.
- Fessler, J. Optimization methods for magnetic resonance image reconstruction: key models and optimization algorithms. IEEE Signal Processing Magazine, 2020;37(1):33-40.
- Borisch, EA, et al. Cross correlation–based misregistration correction for super resolution T2‐weighted spin‐echo images: application to prostate. Magn Reson Med, 2021:85(3):1350-1363.
- Beck, A, et al. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sciences. 2009;2(1):182-202.
Figures

Axial T2SE images of the prostate of one subject: (A) standard 3mm thick T2SE (acquired in 4:14) and (B-F) 1mm thick images. (B) was reconstructed using the linear KZM method[1], while (C-F) were generated with the new MBIR at the λ values shown. Note some improved sharpness of (B) vs. (A) owing to the thinner slice but an increased noise level. MBIR with increasing λ provides progressive reduction in noise in (C-F). However, use of λ=0.00075 caused undesirable blurring, e.g. between the peripheral and transition zones (F, arrow).
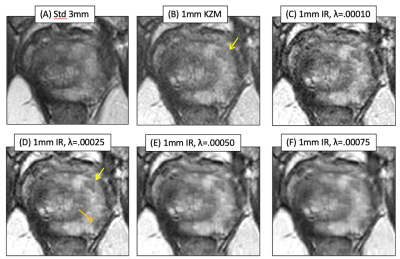
Results from a second case. Fig. 2B vs. A better portrays a lesion (B, arrow), but MBIR provides further improved depiction (D, yellow arrow) and definition of a second lesion (orange arrow). Higher λ values again cause blur. Across the patient studies the radiologist’s perceived preference was for λ=0.00025.