1184
Robust and Computationally Efficient Missing Point and Phase Estimation for Zero Echo Time (ZTE) Sequences1Champaign Imaging LLC, Shoreview, MN, United States, 2University of Iowa, Iowa City, IA, United States
Synopsis
FID sequences such as the zero echo time sequence (ZTE) posses many advantages including capturing signals from fast relaxing spins, efficient use of time and quite acoustic operation. They possess one major disadvantage, information from the start of the FID is nearly always missing or corrupted due to requirements for RF pulse time and T/R switching (ZTE) and gradient ramping (UTE).
Here we modify and apply for the first time a robust and computationally efficient missing point and phase estimation algorithm originating in the solid state NMR community for ZTE imaging sequences.
Introduction:
FID sequences such as ZTE posses many advantages including capturing signals from fast relaxing spins [1], efficient use of time [2; 3] and quite acoustic operation [4; 5]. They possess one major disadvantage, information from the start of the FID is nearly always missing or corrupted due to requirements for RF pulse time and T/R switching (ZTE) and gradient ramping (UTE) [6].Hybrid methods use separate acquisition of the center of K-space, such as in WASPI and PETRA [7]. These methods produce very good results for anatomical scans but limit the ability to acquire dynamic data such as needed for DCE scans or motion correction [8]. Methods such as SWIFT can be used to aquire the center after a small number of acquired views [9] but are difficult to implement on clinical hardware.
Estimation methods potentially offer the optimum solution for regenerate the missing data [7; 10] in dynamic time series acquisions but have issues with numeric stability, especially in the presence of phase variation.
Here we modify and apply for the first time a robust and computationally efficient missing point and phase estimation algorithm originating in the solid state NMR community for ZTE imaging sequences [11].
Methods:
We modified a 3D Radial ZTE sequence to accept table input for view-ordering [12]. All simulated and acquired datasets were reconstructed using 2x oversampled gridding [13] with a radius 4 Kaiser-Bessel kernel and 50 iterations of the Pipe-Menon algorithm for sample density correction [14]. A hollow cube possessing internal slanted sides was simulated by direct synthesis of k-space data and reconstructed by gridding [8]. The modulation transfer function (MTF) in an orthogonal XY slice was estimated with the ImageJ plugin Slanted Edge MTF [15]. Contrast ratio and SNR were evaluated using 32x32 voxel patches in the center slice.2563 1mm3 resolution brain images of a healthy human volunteer were taken using Silent/ZTE using HEALPix view-order with intrinsic T1 weighting, inversion recovery and T2 preparations.
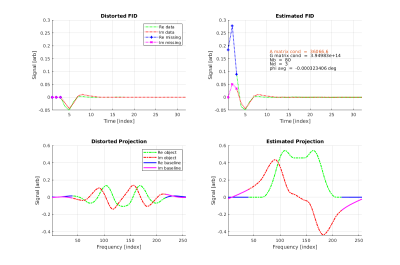
In the Stoch/Olejniczak algorithm [11] the distorted FID has the first Nd missing/distorted points out of N set to zero (see Fig. 1). The distorted projection is generated by FFT of the distorted FID. The algorithm utilizes the Nb point baseline region of the distorted projection, which excludes the region containing the object signal, to estimate the missing points. When the points are correctly estimated this region has minimal real signal. The minimization is accomplished by pseudo inversion of a pre-computed 2*Nd by 2*Nd real matrix, much less numerically onerous than previous methods. Before the missing point estimate the constant phase must first be estimated by an initial deterministic minimization of the real component of the distorted projection utilizing multiplication by an Nb by Nb pre-computed complex matrix.
Results:
Phase and missing point accuracy, Contrast ratio, MTF performance, and SNR were evaluated before and after correction in the simulated cube object for Nd = 0, 1, 2, 3, 4... missing points up until numerical instability (not shown). In-vivo images (Fig 2) were evaluated for SNR and residual artifactual signal surrounding and contaminating the object (Fig. 3).Discussion:
These promising initial results suggest the Stoch/Olejniczak algorithm can open up new possibilities for dynamic and motion corrected ZTE based MRI.Acknowledgements
This work was funded in part by the SBIR Phase I grants R43MH115885 and R43MH122028 from the National Institute of Mental Health. Curt Corum and Champaign Imaging LLC are developing technology related to the topics reported. All in-vivo imaging was performed under an IRB-approved protocol at the University of Iowa, Magnetic Resonance Research Facility. We thank Mr. Stephen Otto of Champaign Imaging LLC for coordination and project management.References
[1] Du,
J.; Bydder, M.; Takahashi, A. M.; Carl, M.; Chung, C. B. and Bydder,
G. M.
(2011).
Short
T2 contrast with three-dimensional ultrashort echo time imaging.,
Magn Reson Imaging 29 : 470-482.
[2] Corum,
C. A.; Bauman, G.; Idiyatullin, D. S.; Hutter, D.; Everson, L. I.;
Eberly, L. E.; Nelson, M. T.; Garwood, M.; Velikina, J. V. and
Samsonov, A. A. (2015).
High
Spatial and Temporal Resolution Breast MRI with 3D Radial SWIFT
Acquisition and Compressed Sensing MOCCO Reconstruction,
(SWIFT-MOCCO).,
.
[3] Corum,
C.; Benson, J.; Idiyatullin, D.; Snyder, A.; Snyder, C.; Hutter, D.;
Everson, L.; Eberly, L.; Nelson, M. and Garwood, M.
(2015).
High
Spatial and Temporal Resolution Breast DCE MRI with SWIFT (SWeep
Imaging with Fourier Transformation): a pilot study,
Radiology 274 : 540-547.
[4] Alibek,
S.; Vogel, M.; Sun, W.; Winkler, D.; Baker, C. A.; Burke, M. and
Gloger, H.
(2014).
Acoustic
noise reduction in MRI using Silent Scan: an initial experience.,
Diagn Interv Radiol 20 : 360-363.
[5] Costagli,
M.; Symms, M. R.; Angeli, L.; Kelley, D. A. C.; Biagi, L.; Farnetani,
A.; Rua, C.; Donatelli, G.; Tiberi, G.; Tosetti, M. and Cosottini, M.
(2016).
Assessment
of Silent T1-weighted head imaging at 7~T.,
Eur Radiol 26 : 1879-1888.
[6] Chiang,
J.-T. A.; Carl, M. and Du, J.
(2013).
Signal
and contrast effects due to T2 decay during k-space readout of UTE
(ultrashort TE) sequences.,
Magn Reson Imaging .
[7] Froidevaux,
R.; Weiger, M.; Brunner, D. O.; Dietrich, B. E.; Wilm, B. J. and
Pruessmann, K. P.
(2017).
Filling
the dead-time gap in zero echo time MRI: Principles compared.,
Magnetic resonance in medicine .
[8] Corum,
C. A.; Kruger, S. J. and Magnotta, V. A.
(2019).
HEALPix
View-order for 3D Radial Self-Navigated Motion-Corrected ZTE MRI,
.
[9] Corum,
C. A.; Idiyatullin, D.; Snyder, C. J. and Garwood, M.
(2015).
Gap
Cycling for SWIFT,
Magn Reson Med 73 : 677-682.
[10] Kuethe,
D. O.; Caprihan, A.; Lowe, I. J.; Madio, D. P. and Gach, H. M.
(1999).
Transforming
NMR data despite missing points.,
J Magn Reson 139 : 18-25.
[11] Stoch,
G. and Olejniczak, Z.
(2005).
Missing
first points and phase artifact mutually entangled in FT NMR
data--noniterative solution.,
Journal of magnetic resonance (San Diego, Calif. : 1997) 173 :
140-152.
[12] Irie,
R.; Suzuki, M.; Yamamoto, M.; Takano, N.; Suga, Y.; Hori, M.;
Kamagata, K.; Takayama, M.; Yoshida, M.; Sato, S.; Hamasaki, N.;
Oishi, H. and Aoki, S.
(2014).
Assessing
Blood Flow in an Intracranial Stent: A Feasibility Study of MR
Angiography Using a Silent Scan after Stent-Assisted Coil
Embolization for Anterior Circulation Aneurysms.,
AJNR Am J Neuroradiol .
[13] Beatty,
P. J.; Nishimura, D. G. and Pauly, J. M.
(2005).
Rapid
gridding reconstruction with a minimal oversampling ratio,
Medical Imaging, IEEE Transactions on 24 : 799 - 808.
[14] Pipe,
J. G. and Menon, P.
(1999).
Sampling
density compensation in MRI: rationale and an iterative numerical
solution.,
Magn Reson Med 41 : 179-186.
[15] Mitja,
C.; Escofet, J.; Tacho, A. and Revuelta, R.
(2011).
Slanted
Edge MTF,
.
Figures
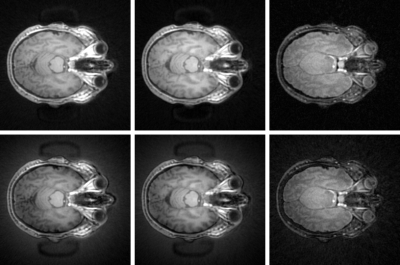
Bottom Row Left to Right: Un-corrected ZTE intrinsic contrast, IR-ZTE and T2-ZTE
Top Row Left to Right: Corrected (Nd = 3) ZTE intrinsic contrast, IR-ZTE and T2-ZTE
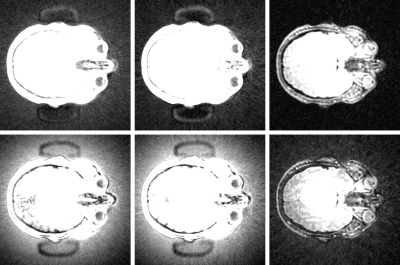
Bottom Row Left to Right: Un-corrected ZTE intrinsic contrast, IR-ZTE and T2-ZTE
Top Row Left to Right: Corrected (Nd = 3) ZTE intrinsic contrast, IR-ZTE and T2-ZTE