Introduction

Undersampling in the spatial frequency domain is a common method to shorten acquisition times in MRI. Thereby, the violation of Nyquist's theorem leads to the emergence of aliasing artefacts which are usually addressed with parallel or auto-calibration methods and most commonly with Compressed Sensing (CS)¹. Especially for three-dimensional applications, resulting long acquisition times often limit clinical applications. The main focus in trajectory design is therefore to achieve an efficient and low-discrepant k-space coverage, which requires the construction of a sampling scheme that leads to an advantageous sampling PSF for the undersampled case^2,3. Ideally, the PSF introduces aliasing artefacts with a noise-like power spectrum for nearly arbitrary undersampling factors. This abstract reports on the aliasing behaviour of a generalised form of the previously introduced "Seiffert Spirals"⁴, using Jacobi theta functions, which allow for a variety of highly adaptable k-space interleaves, while maintaining low-coherent sampling properties. It is furthermore shown, that low-coherent aliasing properties offer the possibility of reconstructing arbitrary FOVs by only introducing random noise-like aliasing artefacts. This leads to a situation in which an MRI trajectory can be constructed by disregarding any desired imaging FOV. Furthermore, the presented concept marks a perfect precondition for the combination with a CS reconstruction.

Methods

The general waveform for one interleave (3D $$$\zeta$$$-based Spiral) is generated on the surface of a unit sphere according to the definition: $$$\zeta: \mathbb{R}_0^+ \rightarrow \mathbb{R}^3$$$, $$$s \mapsto \zeta(s)$$$ with $$$m\in (0,1)$$$ and

\begin{align}\zeta_x(s,m) &= \theta_1(s,m^2)\cdot \cos(s\cdot m^2)\\\zeta_y(s,m) &= \theta_1(s,m^2)\cdot \sin(s\cdot m^2)\\\zeta_z(s,m) &= \theta_2(s,m^2)\end{align}

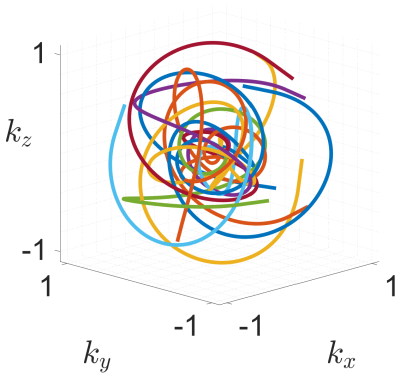
with $$$\theta_1$$$ and $$$\theta_2$$$ being the first two Jacobi theta functions. Furthermore, $$$m$$$ is a parameter to adapt the waveform to hardware limitations such as maximum gradient amplitudes and available slew-rates. The combination with sine and cosine terms allows for a modifiable change in direction per unit length while the symmetry along the $$$z$$$-direction remains unchanged. 15 interleaves of the final trajectory are shown in figure 1.
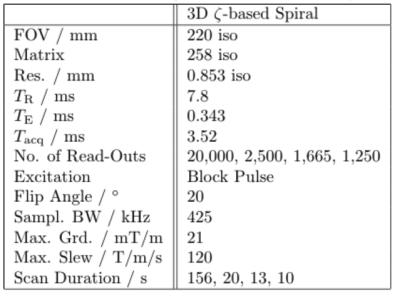
To evaluate the aliasing behaviour as well as imaging performance, an image quality phantom was measured. All phantom images were acquired using a 1.5T wholebody MRI system (Achieva 1.5T, Philips, Best, The Netherlands) and a 16-element SENSE Torso/Cardiac posterior coil. No post-processing, Parallel Imaging or CS was applied to any presented image. The data was only gridded onto a Cartesian grid and Fourier transformed. Undersampling was created by calculating separate and optimised trajectories according to the presented method and parameters with 2,500, 1,665 and 1,250 interleaves, leading to undersampling factors $$$R=8,\,12$$$ and $$$16$$$ with respect to an initial trajectory with 20,000 interleaves ($$$R=1$$$). All relevant scan parameters are listed in table 1.
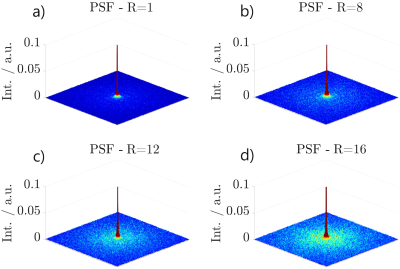
Based on the trajectories, which were used for phantom imaging, sampling point spread functions were calculated according to the undersampling factors $$$R=1,\,8,\,12,\,16$$$ to appreciate aliasing properties.
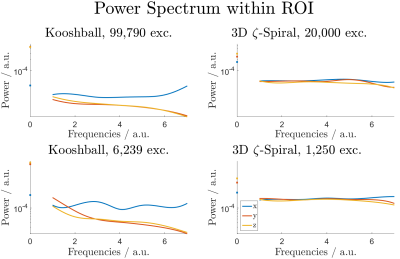
Noise characteristics of the 3D $$$\zeta$$$-based Spiral are compared to 3D radial Kooshball sampling for $$$R=1$$$ and $$$R=16$$$ by calculating the noise power spectrum within a ROI not containing any NMR signal.

Results

Figure 2 shows the point spread functions for the four cases of undersampling in the $$$xy$$$-plane with $$$z=0$$$. By comparing successive undersampling factors, energies in the PSFs emerge that do not seem to follow any ordered or symmetric pattern. Consequently, all PSFs appear to be governed by a low-coherent distribution of energies with an expected aliasing behaviour that is vastly similar to an introduction of white noise. Image sharpness is preserved for all undersampling factors by considering the FWHM of the PSF centre-peak which is $$$\approx 2.544$$$ pixel in width (mean) with a maximum deviation of $$$0.59\,\%$$$ between all undersampling factors.
Figure 3 shows a slice of the image quality phantom, acquired with the presented approach, for each undersampling factor. Each image in figure 3 contains a red square that corresponds to the actual FOV of the underlying 3D $$$\zeta$$$-based Spiral acquisitions. Despite uncorrected coil sensitivity profiles, all images appear non-degraded by coherent aliasing artefacts, especially visible in regions with no phantom fluid.
The noise analysis for a cubic region (ROI) inside the phantom is shown in figure 4. For the 3D $$$\zeta$$$-based Spiral trajectories, all spatial frequency components are about equally represented, leading to a widely flat power spectrum in accordance to the behaviour of white noise. Undersampling in case of the Kooshball trajectory introduces strong modulations in the $$$x$$$-component's power spectrum.

Discussion & Conclusion

In summary, all presented results show dominant low-coherent aliasing properties, leading to a noise-like undersampling behaviour. The equality between the reconstruction of arbitrary FOVs and the possible violation of Nyquist's theorem leads to new imaging strategies or ways in which available scan times can be exploited.
Beneath obvious advantages in scan time reduction, by a combination of undersampling with a CS reconstruction, a variety of new applications and imaging routines seem possible. Using $$$\zeta$$$-based Spirals, a trajectory might be constructed just by following given time restrictions and imaging constraints, e.g. such as:

• Size of k-space sphere is defined by the desired image resolution.

• Maximum read-out duration (spiral length) is defined (limited) by off-resonance behaviour and relaxation effects.

• Total acceptable scan duration defines the number of possible interleaves.

Based on the measured dataset, any feasible FOV can then be reconstructed by introduction of the presented aliasing artefacts.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 research and innovation programme under FETOPEN grant agreement no. 858149. Furthermore, the author's acknowledge the support and sponsorship provided by Philips Healthcare and thank the Ulm University Centre for Translational Imaging MoMAN for its support.