INTRODUCTION

Short-Axis-Propeller (SAP) EPI enables short echo-spacing (ESP), thereby minimizing geometric distortion, while providing low resolution in the readout direction of single blades. Typically, multiple low-resolution blades can be combined to create a final high-resolution EPI image^1-3. However, phase variations among blades and also off-resonance effects that result in blurring remain especially at high field (e.g., 7T). In this work, we extend a recent model-based framework⁴ for reconstructing SAP-EPI to minimize off-resonance induced blurring artifacts. Moreover, locally-low-rank (LLR) regularization⁵ is incorporated to estimate per-blade phase calibrations.

METHODS

I. Discrete Signal Model for Single-Blade SAP-EPI: EPI uses high readout bandwidths such that $$$ \Delta{t}<<T$$$, where $$$\Delta{t}$$$ and $$$T$$$ are dwell time and echo-spacing, respectively - thus $$$\Delta{t}\approx{0}$$$ can be assumed, thereby off-resonance effects primarily manifest along the phase-encoding direction. With discretizing⁶, time-segmenting⁷, and polarity flipping, the single-blade SAP-EPI signal measured during readout $$$m\in [0\,M]$$$ of phase-encoding line $$$n\in [0\,N]$$$ can be modeled as: $$g_{c,\alpha}[m,n]=\sum_{l=0}^{L}Λ_{l}(n)\left\{\sum_{p=0}^{P-1}\sum_{q=0}^{Q-1}s_c[p,q]u[p,q]e^{-j(\triangle{w_0}[p,q][\curlyvee_l-\frac{N-1}{2}]T}e^{-j(k_{x,\alpha}[m]p+k_{y,\alpha}[n]q))}\right\}+\epsilon_{c,\alpha}[m,n]---(1)$$
where $$$Λ_{l}$$$ is a spectral window, $$$\curlyvee_l$$$ denotes the center of segment $$$l$$$ and $$$p\in[0\,P]$$$ and $$$q\in[0\,Q]$$$ are pixel indices. $$$u$$$ is the complex-valued target image, $$$k_{x,\alpha}$$$ and $$$k_{y,\alpha}$$$ are the k-space coordinates in the readout and phase-encoding dimensions associated with blade angle $$$\alpha$$$. $$$s_c$$$ is the sensitivity profile for coil $$$c\in[0\,C-1]$$$, $$$\triangle{w_0}$$$ is the off-resonance, and $$$\epsilon$$$ is Gaussian noise. Defining $$$W_l=diag\left\{e^{-j(\triangle w_0[p,q][\curlyvee_l-\frac{N-1}{2}]T}\right\}$$$ and $$$S=[diag\left\{S_0\right\}\cdots{diag}\left\{S_{C-1}\right\}$$$, Eq. (1) abstracts to:
$$G_\alpha=\left(I{\otimes}\sum_{l=0}^{L}Λ_lF_\alpha{W_l}\right)Su_\alpha+\epsilon_\alpha=A_\alpha{u_\alpha}+\epsilon_\alpha---(2)$$
where $$$F_\alpha$$$ is the Fourier transform (or type-II NUFFT) and $$$\otimes$$$ is Kronecker’s product.

II. Joint Multi-blade Image Reconstruction with virtual-coil LLR: The virtual-coil LLR^8,9 is performed to handle partial Fourier sampling. A set of target images ($$$u_\alpha$$$) are obtained by minimizing the following convex cost function.
$${\min_{\left\{u_1,...u_{N_\alpha}\right\}\in{\mathbb{C}}}}{\left\{\beta\sum_{b\in{\Psi}}\parallel{R_b}(\sum_{\alpha=1}^{N_\alpha}(u_\alpha\delta_\alpha^T+\overline{u_\alpha}\delta_{\alpha+N_\alpha}^T))\parallel_{*}+\sum_{\alpha=1}^{N_\alpha}\parallel{A_\alpha}{u_\alpha}-G_\alpha\parallel_2^2\right\}---(3)}$$
$$$\beta>0$$$ is a regularization parameter. $$$\delta$$$ is Kronecker delta. Operator $$$R_b$$$ extracts the $$$b^{th}\,(B^2\times2N_\alpha)$$$ blocks from the set $$$\Psi$$$ and reshapes each block into Casorati-matrix. Note that there are $$$2N_\alpha$$$ blades in total, including actual acquired blades and virtual blades with “$$$\bar{u}$$$ ” denoting complex-conjugation. The nuclear norm ($$$\parallel\cdot\parallel_*$$$) is the convex envelope of the rank functional. The optimization problem in (3) can be solved using fast composite splitting algorithm¹⁰ (FCSA), a generalization of the Fast Iterative Shrinkage Algorithm (FISTA) that allows independent management of penalties, which herein coincides with blockwise singular value thresholding (SVT) of the (conjugate) augmented Castorati matrices along with aggregation of nominal and virtual blade blocks.

III. Data Acquisition and Processing: In-vivo experiments were performed on a whole‐body 7T-MRI scanner (Siemens Healthcare, Erlangen, Germany) equipped with a gradient coil type SC72AB (70mT/m and 200 T/m/s) using a 32‐channel head-coil (Nova Medical, Wilmington, MA, USA). A healthy-volunteer was scanned after informed consent according to institutional review board-approved (IRB) protocol. six-echo SPGR and single-shot EPI were acquired using vendor-provided sequences. For ssEPI, the FOV was tilted eight times with different angles (22.5 degree each), resulting in SAP-EPI acquisition where readout is 64 samples, 256 phase-encoding steps, 6/8 partial Fourier, and SENSE-factor of 4. SPGR data were utilized for estimating the B0-field-map via fat-water separation toolbox¹¹. In addition, coil sensitivity maps were estimated from their first echo data using the ESPIRiT technique¹². The proposed MBIR was performed in Matlab using 20 iterations of FISTA with manually optimized $$$\beta\,(\beta=0.02)$$$, block-size 7⨯7, 2X-oversampled type-II NUFFT with a width $$$J=5$$$ Kaiser-Bessel kernel, and $$$L=N_{­PE}$$$ time segments. Ramp sampling and odd-even phase correction was performed offline prior to MBIR.

RESULTS

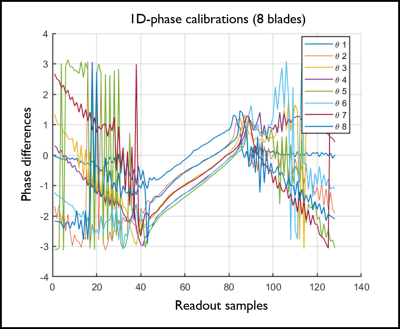
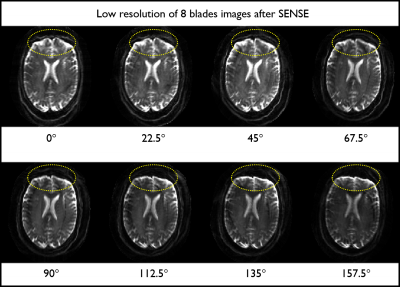
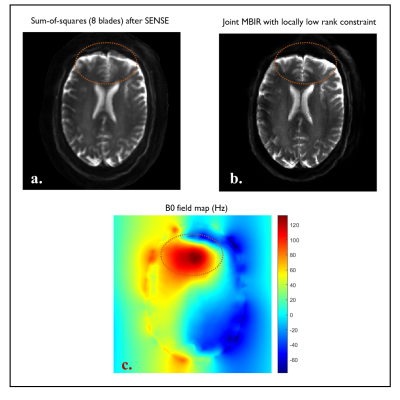
RESULTS: Fig. 1 shows 1D-phase differences between positive and negative readout echoes corresponding to the eight blades with different angles. After being fitted by magnitude weighted least squares, their slopes and intercepts are in the ranges of $$$[0.026\,0.031]$$$ and $$$[-2.54\,-1.62]$$$, respectively. Fig. 2a shows blade specific images obtained using standard SENSE reconstruction. These images look slightly blurry since only 64 samples along the readout were acquired and used to create 256x256 images after zero padding. The yellow circles highlight the geometric distortions that appear differently at different blade angles. The magnitude combination of eight blade images is shown in Fig. 3a, where the blurring artifact is highly visible, particularly in strong B0 field inhomogeneity regions highlighted by the red-circle (Fig. 3c), with up to 120 Hz. Fig. 3b shows that the proposed reconstruction can provide promising results – the blurring artifacts appear much reduced (red-circle) and the resolution is visibly improved.

DISCUSSIONS

The proposed extended version of MBIR with LLR enables high-resolution SAP-EPI images with no need for phase calibration of different multi-blade directions. Typically, N/2-Nyquist ghosting in oblique-FOV-EPI is visible after standard 1D-phase correction due to cross-term gradient induced non-linear phase errors. However, in this study the 1D zeroth and first orders phase correction appears sufficient. This may be due to the use of short readout time, thus higher than first orders phase errors may be negligible. Highly accurate B0 field maps are crucial for the proposed scheme. Thus, highly effective technique in creating B0 maps, such as PSF¹³ may help to improve the image quality even further. It has been discussed how many shots/blades are sufficient for LLR. This point will be further investigated in future studies. Finally, the computational time is proportional to the number of blades, time segments and coil numbers. These issues may be handled by parallel-computing and coil compression¹⁴, respectively.

Acknowledgements

This work was supported by NIH U01 EB024450 and SFB 1436 project Z02.