Introduction

Multi-shot Echo Planar Imaging (EPI) is often applied to reduce off-resonance induced geometric distortion in diffusion weighted (DW) imaging. Ghosts from shot-to-shot phase caused by motion sensitizing diffusion gradients can be resolved with phase correction prior to shot combination^1,2, or without explicit phase estimation using low-rank regularizers in k-space³ or image domain⁴. The application of low-rank regularizers for reconstructing multi-shot DW data has been limited to 2D EPI data, which must be uniformly sampled to maintain constant ky velocity.

In this work, we show that the correct choice of Cartesian sampling trajectory can greatly enhance image quality in an image domain locally low-rank reconstruction^4,5. Data is acquired with a distortionless, diffusion prepped, multi-shot 2D Fast Spin Echo (FSE) sequence. Multi-shot FSE permits modification of sampling patterns in ky-shot space and reduces T2 blurring effects compared to single-shot FSE.

First, we tested a random sampling pattern that creates incoherent aliasing in y-shot space. Compressed sensing reconstructions exploiting sparsity in certain dimensions are known to benefit from noise-like aliasing⁶. We then tested a trajectory that incorporates the center two k-space lines at the beginning of each randomly sampled shot. This was inspired by calibrationless imaging work, which show improved reconstruction quality with the addition of a few center lines^7,8. Prospective reconstructions were compared to shot combination using phase navigators acquired at the end of each echo train. Sampling patterns are shown in Figure 1. We also compared to FSE-PROPELLER, which achieves distortionless DW images using a hybrid radial-Cartesian trajectory at the cost of 1.5x more excitations to fully cover k-space.

Methods

Cartesian DW data was acquired using a diffusion prepared, twice refocused M1 nulled 2D FSE sequence shown in Figure 2a. Non-CPMG magnetization caused by random phase from diffusion gradients was eliminated using a stimulated echo preparation⁹.

Simulated and prospective multi-shot data were reconstructed using Shot Locally Low Rank (SLLR), which frames the shot combination as a calibrationless reconstruction. Shot images are treated as coil images, and varying phase between shots is analogous to unknown coil sensitivities^4,5. SLLR minimizes Equation (1), where $$$D_i$$$, $$$x_i$$$, and $$$y_i$$$ are respectively the sampling operator, shot image to reconstruct, and acquired multi-channel data of the $$$i$$$th shot; $$$F$$$ is the Fourier transform; $$$S$$$ is the sensitivity map; $$$\lambda$$$ is the regularization parameter; and $$$\Omega$$$ Is the set of nonoverlapping blocks. The $$$R_b$$$ operator collects a local patch of coil-combined shot images to form a spatial-shot matrix, shown in Figure 2b.

$$\min_{x_{1\cdots N_{shots}}}\sum_{i=1}^{N_{shots}}\parallel{D_iFSx_i-y_i}\parallel^2_2+\lambda\sum_{k\in\Omega}\parallel{R_b(x_{1\cdots N_{shots}})}\parallel_*\qquad\qquad(1)$$

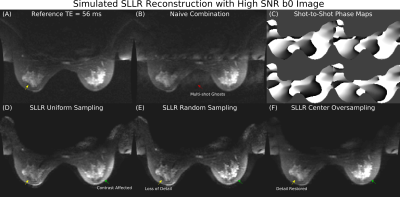
Uniform, random, and center-oversampled patterns were tested in simulation using a T2-weighted breast image, matrix 128$$$\times$$$128, $$$N_{shots}$$$ 12. Shot-to-shot phase maps from phase navigators acquired during DW imaging of the subject were applied to simulate motion-induced phase variations.

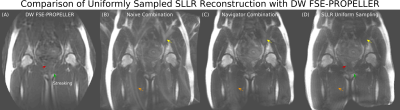
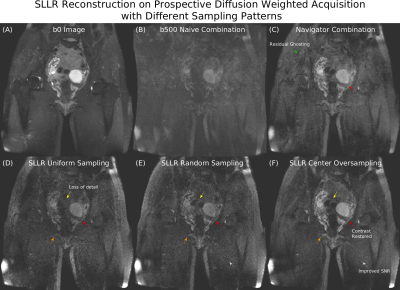
Sampling patterns were applied prospectively in the pelvis of two female volunteers with informed consent and IRB approval. Acquisition parameters were: matrix 128$$$\times$$$128, 38 cm FOV, 8 shots, ETL 16 + (4 for navigator, 2 if center oversampled), slice thickness 5 mm, b-value 500 s/mm², TR 8000 ms, ESP 6 ms, preparation TE 50 ms, refocusing flip angle 120°, readout BW ±50 kHz, 3T (GE Signa Premier). DW FSE-PROPELLER with identical matrix size and matching scan time was collected for comparison. A higher resolution 12-shot scan with matrix 192$$$\times$$$192 was also performed.

Coil sensitives were estimated with ESPIRIT¹⁰ from b0 images. The $$$\lambda$$$ that provided the best reconstruction quality without block-like artifacts was $$$\lambda=0.001$$$ for uniform density, and $$$\lambda=0.01$$$ for center oversampled data with a 5$$$\times$$$5 window.

Results

Simulated SLLR reconstructions in high SNR data are shown in Figure 3. Uniformly and randomly sampled data do not recover all details and have altered contrast. SLLR reconstruction in center oversampled data corrects these artifacts and matches the reference.

Figure 4 compares a uniformly sampled 8-shot SLLR reconstruction with a time matched DW FSE-PROPELLER. SLLR has improved detail compared to FSE-PROPELLER, which has noticeable streaking. SLLR reconstruction has improved ghost reduction compared to the navigator combination, which has residual ghosts from subcutaneous fat.

Figure 5 compares different sampling patterns in a 12-shot acquisition. Uniform sampling has loss of structure in low SNR regions, which is partially corrected with random sampling and further improved with center oversampling. Uniform and random sampling have reduced organ contrast, which is corrected with center oversampling.

Discussion

We have shown that FSE sampling patterns can be modified to complement low-rank reconstructions. Random ky sampling improves detail in low SNR areas, and center oversampling preserves contrast in acquisitions with a high number of shots, which are required to mitigate T2 blurring effects prominent in single-shot FSE. This may be due to uniform sampling missing the contrast-rich k-space center when the number of shots is high. Although the acquisition time of DW FSE is 1.5-2$$$\times$$$ longer than EPI due to gradient heating, FSE eliminates distortion in the phase encode direction. This can be applied to off-resonance environments where multi-shot EPI would fail, such as DW imaging near metallic breast biopsy clips, hip prostheses, and gas filled bowel loops.

Conclusion

Sampling patterns in Cartesian DW FSE can be modified to improve low-rank reconstructions. Cartesian DW FSE is more time efficient than FSE-PROPELLER and has less geometric distortion than EPI.

Acknowledgements

R01 EB009055. GE Healthcare. Karolinska Neuro MR Physics group for pulse programming assistance.