1179

Accelerating gSlider-based Diffusion MRI: Phase constraints enable reduced RF encoding

Yunsong Liu¹, Kawin Setsompop², and Justin P. Haldar¹
¹Signal and Image Processing Institute, University of Southern California, Los Angeles, CA, United States, ²Department of Radiology, Stanford University, Stanford, CA, United States

Synopsis

gSlider is an efficient technique for diffusion MRI that uses multiple RF encodings to encode high-resolution spatial information along the slice dimension. In this work, we investigate whether smooth-phase constraints can be used to reduce the required number of RF encodings. Although smooth-phase constraints are classically used to reduce k-space sampling (partial Fourier acquisition), we believe that their use to reduce RF encoding requirements is novel. Theoretical and simulation results demonstrate that, if optimized RF encodings are used, phase constraints can successfully be used to reduce the number of required RF encodings in image regions where the phase is smooth.

Introduction

gSlider is a technique that enables high-resolution diffusion MRI with state-of-the-art efficiency^1,2. High SNR-efficiency is enabled by exciting thick slabs while using multiple RF encodings to resolve the thin slices that constitute each slab. In conventional gSlider, the number of RF encodings is required to be equal to the number of thin slices. Unfortunately, using a large number of RF encodings requires the experiment to be long. Recently, constrained reconstruction methods have been proposed to accelerate gSlider that reduce the number of RF encodings by exploiting the correlation between q-space samples^3-5.
In this work, we consider a novel and complementary approach to reducing the number of RF encodings. Specifically, we consider the use of smooth phase constraints. While phase constraints are classical for accelerated k-space acquisitions (i.e., partial Fourier acquisition^6,7), we believe they have not been previously applied to accelerate RF-encoded experiments.

Methods

Data acquisition for gSlider can be modeled as
$$b_{r}(\mathbf{x}_{n})= e^{i \phi_r(\mathbf{x}_n)} \sum_{s=1}^Sg_{rs}m_s(\mathbf{x}_n)+z_{rn},$$
where $$$b_{r}(\mathbf{x}_{n})$$$ is the thick-slab data measured for the $$$r$$$th RF encoding ($$$r=1,\ldots,N_{RF}$$$) at voxel location $$$\mathbf{x}_{n}$$$ ($$$n=1,\ldots, N_v$$$), $$$g_{rs}$$$ represents the RF encoding applied to the $$$s$$$th thin slice ($$$s=1,\ldots,N_s$$$) by the $$$r$$$th RF encoding, $$$m_s(\mathbf{x}_n)$$$ represents the magnitude of the $$$s$$$th thin slice at voxel location $$$\mathbf{x}_n$$$, $$$\phi_r(\mathbf{x}_n)$$$ represents the measured image phase for the $$$r$$$th RF encoding (which is random due to the physics of diffusion acquisition), and $$$z_{rn}$$$ represents measurement noise.
In conventional gSlider, the number of RF encodings $$$N_{RF}$$$ is taken to be greater than or equal to the number of thin slices $$$N_s$$$. In this work, we evaluate whether assuming that the phase is smooth can enable reduced RF encoding.
We approach this question in two different ways. First, we evaluate the Cramer-Rao bound (CRB), which is an estimation-theoretic tool that can be used to estimate uncertainty in parameter estimation and can also be used to optimize acquisition strategies⁸. CRBs were calculated as a function of the number of voxels in a local image patch, under the strong assumption that all voxels within the patch shared the same phase, both in-plane and along the slice dimension. Using a larger patch corresponds to stronger phase smoothness assumptions. As part of this process, we also use the CRB to optimize the RF encoding parameters $$$g_{rs}$$$ in order to maximize the ability to accurately estimate the thin-slice image magnitudes. In addition, we also simulated phase-constrained gSlider reconstruction, where we used quadratic regularization of the image phases to impose soft constraints on the phase. This phase regularization was implemented using a variation of the algorithm in Ref. 9. For reference, we also implemented a minimum-norm reconstruction that did not enforce smooth phase constraints.

Results

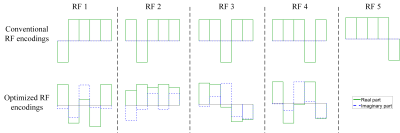
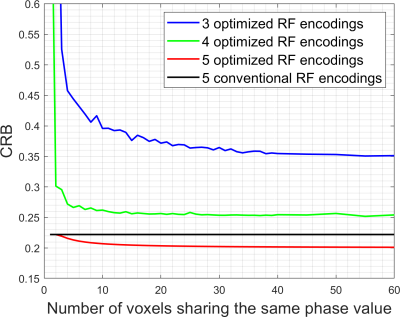
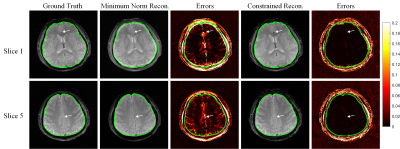
Figure 1 shows the RF excitation profiles for conventional gSlider with 5 RF encodings to resolve 5 slices. The figure also shows the set of RF excitation profiles we obtain after optimizing the CRB to resolve 5 slices using 4 RF encodings with phase constraints. Figure 2 plots the CRB as a function of the number of in-plane voxels sharing the same phase. We observe that the original gSlider RF encoding strategy does not benefit from smooth phase constraints, but that the optimized strategies can improve substantially from assuming smooth phase constraints. This observation is potentially surprising, although we have derived theoretically that phase constraints will never have an impact on the CRB if the RF encoding coefficients $$$g_{rs}$$$ are all real-valued (as they were in the original gSlider implementation). For the CRB to benefit from phase constraints, it is theoretically necessary to use complex-valued RF encoding. Importantly, we also observe that using 4 optimized RF encodings with phase constraints to resolve 5 slices is theoretically not that much worse than using 5 RF encodings.
Figure 3 shows representative simulation results (based on complex-valued T2-weighted brain data) using 4 optimized RF encodings to reconstruct 5 slices. It can be observed that the brain parenchyma (inside the green outline) is reconstructed well when using phase constraints, while the minimum-norm reconstruction unsurprisingly has noticeable errors in this underdetermined setting. The phase constrained reconstruction has more substantial errors outside the brain parenchyma, which we believe occurs because the phase becomes non-smooth as we move from the brain into the skull and scalp.

Discussion and Conclusions

The use of phase constraints is a viable mechanism to reduce the number of RF encodings in gSlider in spatial regions where the image phase is smooth, and is likely complementary to other constraints that have been used to improve the quality of gSlider reconstruction^3-5,10. Although our results are promising, a potential limitation of this study is that we assumed ideal RF excitation profiles for both theoretical analysis and simulation, and only showed retrospective results. An important next step will be to validate that these results can be achieved practically with prospectively-acquired data.

Acknowledgements

This work was supported in part by research grants NIH R01-MH116173 and NIH R01-NS074980, as well as a USC Viterbi/Graduate School Fellowship.

References

[1] Setsompop K, Fan Q, Stockmann J, Bilgic B, Huang S, Cauley SF, Nummenmaa A, Wang F, Rathi Y, Witzel T, Wald LL. “High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (gSlider-SMS).” Magn Reson Med 79:141-151, 2018.

[2] Liao C, Stockmann J, Tian Q, Bilgic B, Arango NS, Manhard MK, Huang SY, Grissom WA, Wald LL, Setsompop K. High‐fidelity, high‐isotropic‐resolution diffusion imaging through gSlider acquisition with and corrections and integrated shim array. Magn Reson Med 83:56-67, 2020.

[3] Haldar JP, Setsompop K. “Fast high-resolution diffusion MRI using gSlider-SMS, interlaced subsampling, and SNR-enhancing joint reconstruction.” Proc. ISMRM 2017, p. 175.

[4] Liu Y, Liao C, Setsompop K, Haldar JP. “An evaluation of q-space regularization strategies for gSlider with interlaced subsampling.” Proc. ISMRM 2020, p. 4368.

[5] Ramos-Llorden G, Ning L, Liao C, Mukhometzianov R, Michailovich O, Setsompop O, Rathi Y. High‐fidelity, accelerated whole‐brain submillimeter in vivo diffusion MRI using gSlider‐spherical ridgelets (gSlider‐SR). Magnetic Resonance in Medicine 84:1781-1795, 2020.

[6] Liang Z-P, Boada F, Constable T, Haacke EM, Lauterbur PC, Smith MR. Constrained reconstruction methods in MR imaging. Rev Magn Reson Med 4:67-185, 1992.

[7] Haldar JP, Setsompop K. Linear predictability in magnetic resonance imaging reconstruction: Leveraging shift-invariant Fourier structure for faster and better imaging. IEEE Signal Process Mag 37:69-82, 2020.

[8] Kay SM. Fundamentals of Statistical Signal Processing. Volume I: Estimation Theory. Prentice Hall, 1993.

[9] Liu Y, Haldar JP. NAPALM: An Algorithm for MRI Reconstruction with Separate Magnitude and Phase Regularization. Proc. ISMRM 2019, p. 4764.

[10] Haldar JP, Liu Y, Liao C, Fan Q, Setsompop K. Fast submillimeter diffusion MRI using gSlider-SMS and SNR-enhancing joint reconstruction. Magn Reson Med 84:762-776, 2020.

Figures

Figure 1. RF excitation profiles corresponding to (top) the original gSlider RF encoding scheme to resolve 5 thin slices from 5 RF encodings, and (bottom) the CRB-optimized RF encoding scheme to resolve 5 thin slices from 4 RF encodings with phase constraints. Note that all sub-slices are excited with a full magnitude of 1 in all cases.

Figure 2. CRBs for resolving 5 thin slices as a function of the number of voxels sharing the same phase value, plotted for several different RF encoding strategies. Note that without phase constraints, the CRB blows up to infinity whenever the number of RF encodings is smaller than the number of thin slices (5 in this case).

Figure 3. Simulated reconstruction of 5 thin slices from the set of 4 optimized RF encodings, for both phase-constrained and minimum norm reconstruction. For ease of visualization, we only show two out of the five reconstructed slices for each case.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1179