1178
Optimal Transport Based Convex Hybrid Image and Motion-Field Reconstruction1Institute of Medical Engineering, TU Graz, Graz, Austria, 2Solgenium OG, Linz, Austria, 3Department of Information and Communications Technologies, Pompeu Fabra University, Barcelona, Spain, 4Institute of Mathematics and Scientific Computing, NAWI Graz, University of Graz, Graz, Austria, 5BioTechMed-Graz, Graz, Austria
Synopsis
In this study we present an approach that combines sub-sampled encoding reconstruction and simultaneous object motion computation. For that purpose Optimal Transport is used as convex regularization for motion-afflicted measurements. It reconstructs explicit pixel-wise motion fields simultaneously to the image series. Results based on simulated data show that 8-frame image series can be reconstructed in great detail from 4-fold undersampled k-space series data from a single coil. The high potential of the presented method could be shown for the reconstruction of undersampled image series. For the recovery of the motion fields, further improvements are still necessary.
Introduction
Subject motion is an ongoing problem in the clinical and scientific field of MRI. Solutions have come from hardware improvements, sequence design and reconstruction techniques [1,2,3]. In reconstruction, when faced with non-rigid motion, there are two common approaches. The first one separates data into a time- or motion-series of k-spaces and corrects for motion implicitly through regularization along space and time axes (e.g.[4,5]). The second one uses an explicit motion model to reverse the motion effects during reconstruction (e.g.[6,7]). Here, we propose a novel approach that aims to combine regularization along a motion axis together with explicit motion models. A concept from Optimal Transport (OT) is used as regularization along a time-series of k-spaces. The needed explicit pixel-wise motion field is reconstructed together with the image series. This approach is especially well-suited for dynamic MRI of relative slow moving objects (e.g. kidney) where images must be reconstructed from a series of undersampled k-spaces.Theory
Defining a real, non-negative image series $$$\rho(\vec{x},t)$$$ with the matching velocity field $$$\vec{v}(\vec{x},t)$$$ and the momentum field $$$\vec{m}=\rho\vec{v}$$$, the OT cost can be defined as\begin{align}J(\rho(\vec{x},t),\vec{m}(\vec{x},t))=\sum\limits_{\vec{x},t}\frac{|\vec{m}(\vec{x},t)|^2}{\rho(\vec{x},t)}.\end{align}For $$$\rho(\vec{x},t)=0$$$ and $$$\vec{m}(\vec{x},t)=0$$$ we set $$$\frac{|\vec{m}(\vec{x},t)|^2}{\rho(\vec{x},t)}=0$$$ and for $$$\rho(\vec{x},t)=0$$$ and $$$\vec{m}(\vec{x},t)\neq 0$$$ we set $$$\frac{|\vec{m}(\vec{x},t)|^2}{\rho(\vec{x},t)}=\infty$$$. The variational problem for reconstruction of a time-series of k-spaces $$$d_k$$$ is then given as \begin{align}\min\limits_{(\rho,m)\in\mathcal{C}}&\left[\sum\limits_k\lambda||\mathcal{F}_k(\rho)-d_k||^2_2\right]+J(\rho(\vec{x},t),\vec{m}(\vec{x},t)),\\ \mathrm{s.t.}\:&\rho(\vec{x},t)\in\mathbb{R}_{\geq 0}\end{align}where $$$\mathcal{F}_k$$$ is the forward operator including the coil sensitivities, Fourier Transform and sampling pattern of $$$d_k$$$. A solution $$$(\rho^*,m^*)$$$ must be in $$$\mathcal{C}$$$, the set of solutions fulfilling the continuity equation $$$\partial_t \rho + \vec{\nabla} \vec{m}=0$$$. It can be shown that this problem promotes sparsity in each image frame and intrinsically recovers the momentum field during reconstruction [8]. Contrary to many reconstruction problems involving explicit motion models [9], this problem is convex and guarantees stable solutions [8].Methods
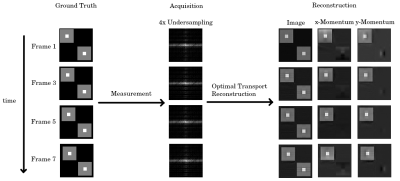
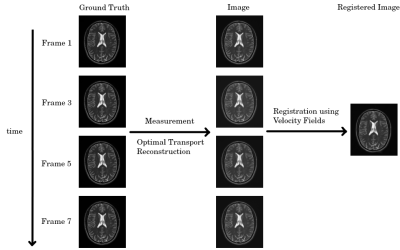
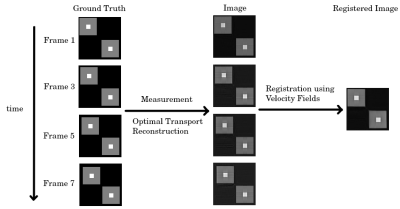
To solve the above stated minimization problem, a primal-dual algorithm was implemented [10] which yields the reconstructed image series and the pixel-wise momentum fields describing inter-frame movement (figure 1). The calculation of the velocity field via $$$\vec{v}=\frac{\vec{m}}{\rho}$$$ (for $$$\rho\neq0$$$) is unstable in application due to division by small values and noise in the images. Thus, the velocity field is additionally de-noised with a Total Variation algorithm after division. To simulate measurements, three different 2D image series were created. First, two $$$100\times100\times8$$$ noiseless, synthetic images were made containing basic stationary, linearly moving, and rotating objects. Then, from a single high-resolution MR brain image, a $$$512\times464\times8$$$ series was created with small, affine motion added in-between frames. Those series were turned into single-coil k-space data from which each 2D k-space was retrospectively undersampled by a factor of 4 with 8 additional center lines measured. The algorithm, initialized with the images from the zero-filled k-spaces and all-zero momentum fields, was then tasked to reconstruct the data. For testing the quality of the velocity field, all time frames were registered onto the first frame using only the motion information from the velocity fields.Results/Discussion
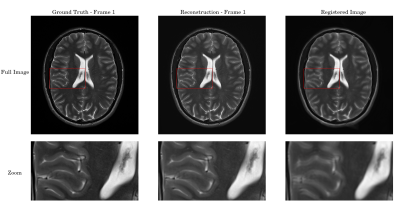
For the brain data (figures 2 and 3), the reconstructed images show an excellent quality, mirroring the ground truth in great detail. The registered image shows blurring, signaling a potential problem with the velocity field. The quality of the velocity field can be better examined in a simpler environment. In the registered images of the synthetic data sets (figures 4 and 5), it can be seen that the stationary and translated objects are accurately registered while the rotating object shows artifacts. The reconstructed image series are close to the ground truth except for small streaking artifacts. Considering the three reconstructed image series, using only the OT concept as regularization, each image in the series could be reconstructed from a single-coil, 4-fold undersampled k-space. This proves that this new reconstruction constraint accurately exploits sparsity in MR-reconstruction to recover unmeasured information in a time-series. In the brain images, even great detail is resolved. In the registered image, it becomes apparent that the recovered velocity fields accurately depict translation and do not alter stationary objects, but rotations produce artifacts. In our current understanding we suspect that the reconstructed momentum field is correct, but the calculation of the velocity field from the momentum field, including TV denoising, produces the artifacts. A possible solution is being worked on which includes alternate denoising approaches. Still, the rotating square shows that the velocity fields follow the motion as a whole, but imperfections produce blurring.Conclusion/Outlook
While the results so far are only based on simulation, this novel approach shows exciting promise for image reconstruction. Images in a motion-afflicted time-series could be recovered in detail from heavily undersampled single-coil k-spaces using only OT regularization. This proves the viability of this new concept. For the future, testing the reconstruction on in-vivo data with an appropriate sequence is the first priority. The reconstruction from multi-coil data, which is already possible with the algorithm, will improve results. Then, combining the OT functional with additional regularizers (e.g. TV) may further enhance reconstruction. Importantly, the calculation of the velocity field from the momentum field must be optimized. Finally, there are methods to adapt this algorithm for special situations where the continuity equation is not fulfilled [8] (e.g. DCE-MRI, through-plane motion). These remain to be implemented and tested.Acknowledgements
The authors gratefully acknowledge support by the Christian Doppler Research Association (CDG) and Austrian Science Fund (FWF) through the Partnership in Research project PIR-27 “Mathematical methods for motion-aware medical imaging”.References
1: Maxim Zaitsev, Julian Maclaren, and Michael Herbst. Motion artifacts in MRI:A complex problem with many partial solutions. Journal of Magnetic Resonance Imaging, 42(4):887–901, 2015.
2: F Godenschweger, U Kägebein, D Stucht, U Yarach, A Sciarra, R Yakupov,F Lüsebrink, P Schulze, and O Speck. Motion correction in MRI of the brain. Physics in Medicine & Biology, 61(5):R32, 2016.
3: Li Feng, Thomas Benkert, Kai Tobias Block, Daniel K Sodickson, Ricardo Otazo, and Hersh Chandarana. Compressed sensing for body MRI. Journal of Magnetic Resonance Imaging, 45(4):966–987, 2017.
4: Li Feng, Leon Axel, Hersh Chandarana, Kai Tobias Block, Daniel K Sodickson,and Ricardo Otazo. XD-GRASP: golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magnetic Resonance in Medicine, 75(2):775–788, 2016.
5: Lorenzo Di Sopra, Davide Piccini, Simone Coppo, Matthias Stuber, and Jérôme Yerly. An automated approach to fully self-gated free-running cardiac and respiratory motion-resolved 5D whole-heart MRI. Magnetic Resonance in Medicine,82(6):2118–2132, 2019.
6: Freddy Odille, Pierre-André Vuissoz, Pierre-Yves Marie, and Jacques Felblinger.Generalized reconstruction by inversion of coupled systems (GRICS) applied to free-breathing MRI. Magnetic Resonance in Medicine, 60(1):146–157, 2008.
7: Michael S Hansen, Thomas S Sørensen, Andrew E Arai, and Peter Kellman.Retrospective reconstruction of high temporal resolution cine images from real-time MRI using iterative motion correction. Magnetic Resonance in Medicine,68(3):741–750, 2012.
8: Kristian Bredies and Silvio Fanzon. An optimal transport approach for solving dynamic inverse problems in spaces of measures. ESAIM: Mathematical Modelling and Numerical Analysis, 54(6):2351–2382, 2020.
9: Jean-David Benamou and Yann Brenier. A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem. Numerische Mathematik, 84(3):375–393, 2000.
10: Antonin Chambolle and Thomas Pock. A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision, 40(1):120–145, 2011.
Figures